Using the formula for the volume of rotation bodies, we calculate the volume of the ball.
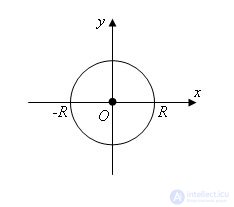
We introduce Cartesian coordinates, taking the center of the ball to the origin. The xy plane intersects the surface of a sphere of radius R in a circle defined by the formula
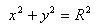
The semicircle located above the x axis is given by the equation
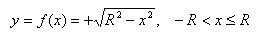
Therefore, the volume of the ball is determined by the formula

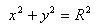
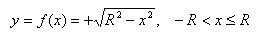
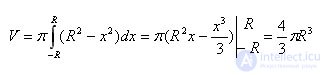
Comments
To leave a comment
Stereometry
Terms: Stereometry