Perpendicular lines in space

Theorem

If two intersecting lines are parallel, respectively, to two perpendicular straight lines, then they are perpendicular.



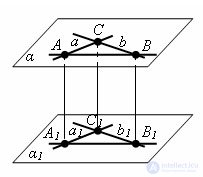
Evidence

Let a and b be perpendicular lines, a1 and b1 be intersecting lines parallel to them.
If the lines a, b, a1, b1 lie in the same plane, then they have the property specified in the theorem, kA, this is known from planimetry.
Suppose that the lines e lie on the same plane. Then the lines a and b lie in the plane α, and the lines a1 and b1 lie in a plane α1. By the theorem on the feature of parallel straight lines, the planes α and α1 are parallel. Let C be the intersection point of lines a and b, and C the point of intersection of lines a1 and b1. Let us draw in the plane of parallel straight lines a and a1 a straight line parallel to the straight line CC1. It intersects the lines a and a1 at points A and A1. In the plane of straight lines b and b1 we draw a straight line parallel to the straight line CC1, and denote by B and B1 its intersection points with straight lines b and b1.
The CAA1C1 and CBB1C1 quadrangles are parallelograms, since their opposite sides are parallel. The quadrilateral ABB1A1 is also a parallelogram. He has sides AA1, BB1 parallel, because each of them is parallel to the straight line CC1. Consequently, the quadrilateral lies in the plane passing through the parallel straight lines AA1 and BB1. This plane intersects parallel planes α and α1 along parallel straight lines AB and A1B1.
Since the parallelogram of the opposite sides are equal, then AB = A1B1, AC = A1C1, BC = B1C1. Δ ABC = ΔA1B1C1 (on the third sign of equality of triangles). ∠ ACB = ∠A1C1B1 = 90º. Therefore, the lines a1 and b1 are perpendicular. The theorem is proved