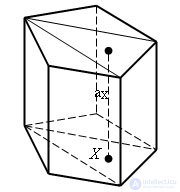
Take an arbitrary prism. Divide its base into triangles. Let Δ be one of these triangles. Let us draw through an arbitrary point X - a triangle Δ a straight line parallel to the side edges. Let ax be the segment of this line belonging to the prism. When the point X describes the triangle Δ, the segments ax fill the triangular prism. By constructing such a prism for each triangle Δ, we obtain a partition of this prism into triangles. All these prisms have the same height, equal to the height of the original prism.
The volume of this prism is equal to the sum of the volumes of the triangular prisms that make it up. According to the proven volume of a triangular prism is equal to the product of its base area and height. Therefore, the volume of the prism is equal to:
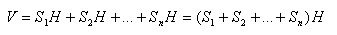
where S1, S2, ..., Sn are the areas of the triangles into which the base of the prism is divided, and H is the height of the prism. Therefore, V = SH.
The volume of any prism is equal to the product of its base area and height.

Comments
To leave a comment
Stereometry
Terms: Stereometry