Theorem
The side surface of a straight prism is equal to the product of the base perimeter and the height of the prism, i.e. on the length of the side edge.
Evidence
The lateral faces of a straight prism are rectangles. The bases of these rectangles are the sides of the polygon lying at the base of the prism, and the heights are equal to the length of the side edges. Therefore, the lateral surface of the prism is
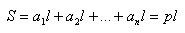
where a1, a2, ..., an are the lengths of the edges of the base, p is the perimeter of the base of the prism, and l is the length of the side edges. The theorem is proved. |
|
Comments
To leave a comment
Stereometry
Terms: Stereometry