Property perpendicular line and plane

Theorem

If the plane is perpendicular to one of two parallel lines, then it is perpendicular to the other.



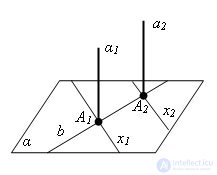
Evidence

Let a1 and a2 be two parallel lines and α be the plane perpendicular to the line a1. Let us prove that this plane is perpendicular to the line a2.
Let us draw through the point A2 of the intersection of the line a2 with the plane α an arbitrary straight line x2 in the plane α. In the plane α through the point A1 of the intersection of the line a1 and α we draw a straight line x1 parallel to the straight line x2. Since the straight line a1 is perpendicular to the plane α, the straight lines a1 and x1 are perpendicular. By the perpendicularity theorem of straight lines in space, the intersecting straight lines a2 and x2 parallel to them are also perpendicular. Thus, the straight line a2 is perpendicular to any straight line x2 in the plane α. This means that the straight line a2 is perpendicular to the plane α. The theorem is proved.