Cone volume

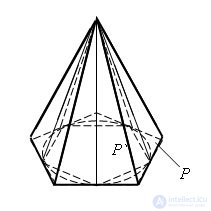
We construct two polygons in the plane of the base of the cone: a polygon P containing the base of the cone and a polygon P` contained in the base of the cone. We construct two pyramids with bases P and P` and a vertex at the apex of the cone. The first pyramid contains a cone, and the second pyramid is contained in a cone.
There are such polygons P and P`, the areas of which with an unlimited increase in the number of their sides n unlimitedly approach the area of ​​the circle at the base of the cone. For such polygons, the volumes of the constructed pyramids unboundedly approach 1/3 SH, where S is the area of ​​the base of the cone, and H is its height. According to the definition, it follows that the volume of the cone



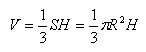
The volume of the cone is equal to one third of the work area of ​​the base to the height.