Theorem The line of intersection of two spheres is a circle.
 Evidence
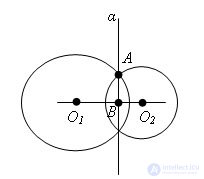
Evidence Let O1 and O2 be the centers of spheres and A be their intersection point. Let us draw through the point A the plane α, perpendicular to the straight line O1O2.
Denote by B the intersection point of the plane α with the straight line O1O2. According to the theorem, the section of the ball by the plane, the plane α, intersects both spheres along the circle K with the center B passing through the point A. Thus, the circle K belongs to the intersection of the spheres.
We prove that the spheres have no other intersection points, except for the points of the circle K. Suppose that the point X of the intersection of the spheres does not lie on the circle K. We draw a plane through the point X and the line O1O2. It will cross the spheres in circles with centers O1 and O2. These circles intersect at two points belonging to circle K, and even at point X. But two circles cannot have more than two points of intersection. Consequently, the intersection of the spheres is a circle. The theorem is proved

Comments
To leave a comment
Stereometry
Terms: Stereometry