Lecture
Information coding is used to unify the presentation of data that are of various types in order to automate the work with information.
Encoding is the expression of data of one type through data of another type. For example, natural human languages can be regarded as coding systems for expressing thoughts through speech, and, moreover, alphabets are coding systems for components of a language using graphic symbols.
In computing, binary coding is used . The basis of this coding system is the presentation of data through a sequence of two characters: 0 and 1. These characters are called binary digits (binary digit), or abbreviated bit (bit). One bit can be encoded two concepts: 0 or 1 (yes or no, true or false, etc.). With two bits it is possible to express four different concepts, and three to encode eight different values.
The smallest unit of coding information in computer technology after bits - bytes. Its connection to the bit reflects the following relation: 1 byte = 8 bits = 1 character.
Usually one character of text information is encoded in one byte. For this reason, for text documents, the size in bytes corresponds to the lexical volume in characters.
The larger unit of information coding is the kilobyte associated with a byte by the following relation: 1 Kb = 1024 bytes.
Other, larger, units of information coding are the symbols obtained by adding the prefixes mega (MB), giga (GB), tera (TB):
1 MB = 1,048,580 bytes;
1 GB = 10 737 740 000 bytes;
1 TB = 1024 GB.
To encode a binary code of an integer, you should take an integer and divide it in half until the quotient is equal to one. The set of residues from each division, which is written from right to left together with the last quotient, and will be the binary analogue of the decimal number.
In the process of encoding integers from 0 to 255, it is enough to use 8 bits of the binary code (8 bits). Using 16 bits allows you to encode integers from 0 to 65,535, and with the help of 24 bits - more than 16.5 million different values.
In order to encode real numbers, 80-bit encoding is used. In this case, the number is pre-converted into a normalized form, for example:
2,1427926 = 0.21427926? 101;
500,000 = 0.5? 106
The first part of the coded number is called the mantissa, and the second part is the characteristics. The main part of 80 bits is allocated for storing the mantissa, and some fixed number of digits is allocated for storing the characteristic.
Byte (English byte ) - a unit for storing and processing digital information; a set of bits processed by a computer at once. In modern computing systems, a byte consists of eight bits and, accordingly, can take one of 256 (2 8 ) different values (states, codes). However, in the history of computer technology there were solutions with different byte sizes (for example, 6, 32 or 36 bits), therefore sometimes the term “octet” (Latin octet ) is used in computer standards and official documents to uniquely identify a group of 8 bits.
In most computational architectures, a byte is the minimum independently addressable data set.
The name “byte” (the word byte is an abbreviation of the phrase BinarY TErm - “binary term” [ source not specified 134 days ] ) was first used in 1956 by V. Buchholz (eng. Werner Buchholz ) when designing the IBM 7030 Stretch first supercomputer for a beam simultaneously transmitted in the input-output devices of six bits. Later, in the framework of the same project, the byte was expanded to eight bits.
A number of computers of the 1950s and 1960s (BESM-6, M-220) used 6-bit characters in 48-bit or 60-bit machine words. In some models of computers manufactured by Burroughs Corporation (now Unisys), the character size was 9 bits. In the Soviet computer Minsk-32 a 7-bit byte was used.
Byte memory addressing was first used in the IBM System / 360 system. In earlier computers, it was only possible to address an entire machine word consisting of several bytes, which made it difficult to process text data.
The 8-bit bytes were taken in System / 360, probably due to the use of the BCD format for representing numbers: one decimal digit (0-9) requires 4 bits (tetrad) for storage; one 8-bit byte can represent two decimal digits. 6-bit bytes can store only one decimal digit, two bits remain unused.
According to another version, the 8-bit byte size is associated with the 8-bit same numeric representation of characters encoded in EBCDIC.
According to the third version, due to the binary coding system in computers, the most favorable for the hardware implementation and convenient for data processing are the word lengths multiple to powers of 2, including 1 byte = 2 3 = 8 bits, systems and computers with word lengths not multiple number 2 have disappeared because of disadvantage and inconvenience.
Gradually, 8-bit bytes became the de facto standard; Since the beginning of the 1970s, bytes in most computers consist of 8 bits, and the size of a machine word is a multiple of 8 bits.
For reasons of convenience, non-text data type units are also made a multiple of eight bits, for example:
The number of states (codes, values), which can take 1 eight-bit byte with positional coding, is determined in combinatorics, is equal to the number of allocations with repetitions and is calculated by the formula:
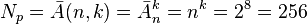 possible states (codes, values), where
possible states (codes, values), where
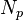 - the number of states (codes, values) in one byte.
- the number of states (codes, values) in one byte.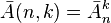 - the number of placements with repetitions.
- the number of placements with repetitions.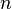 - the number of states (codes, values) in one bit; in bit 2 states (n = 2).
- the number of states (codes, values) in one bit; in bit 2 states (n = 2).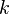 - the number of bits per byte; in the 8-bit byte k = 8 and it can be from 0 to 8 identical bits (repetitions).
- the number of bits per byte; in the 8-bit byte k = 8 and it can be from 0 to 8 identical bits (repetitions).| Measurements in bytes | ||||||||
|---|---|---|---|---|---|---|---|---|
| GOST 8.417-2002 | Prefixes SI | IEC Consoles | ||||||
| Title | Symbol | Power | Title | Power | Title | Symbol | Power | |
| byte | B | 10 0 | - | 10 0 | byte | B | B | 2 0 |
| kilobyte | KB | 10 3 | kilo- | 10 3 | kibibayt | Kib | KiB | 2 10 |
| megabyte | MB | 10 6 | mega- | 10 6 | mebibyte | Mib | MiB | 2 20 |
| gigabyte | GB | 10 9 | giga- | 10 9 | gibibayt | Gib | GiB | 2 30 |
| terabyte | Tb | 10 12 | tera- | 10 12 | tebibayt | TiB | Tib | 2 40 |
| petabyte | PB | 10 15 | peta | 10 15 | pebibayt | PiB | Pb | 2 50 |
| exabyte | EB | 10 18 | exa- | 10 18 | eksbibayt | Eib | E & B | 2 60 |
| Zettabyte | ZB | 10 21 | zetta | 10 21 | zebibyte | ZiB | Zib | 2 70 |
| yotabayte | Yb | 10 24 | yotta- | 10 24 | jobbibit | Yib | YiB | 2 80 |
Multiple prefixes for the formation of derived units for a byte are not used as usual: diminutive prefixes are not used at all, and information units of measure smaller than a byte are called special words (nibble and bit); Magnifying prefixes are multiples of 1024 = 2 10 , that is, 1 kilobyte is 1024 bytes, 1 megabyte is 1024 kilobytes, or 1 048 576 bytes, etc. for gib, tera, and pebbytes. The difference between capacities (volumes), expressed in kilos = 10 3 = 1000 and expressed in kibi = 2 10 = 1024, increases with increasing weight of the console. The IEC recommends using binary prefixes, but in practice they are not yet used, perhaps because of the non-*** ago sound - kibibyte , mebibyte , yobibyt , etc. [ source not specified 995 days ] .
Sometimes decimal prefixes are used in the literal sense, for example, when specifying the capacity of hard drives: they have gigabytes may not mean 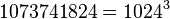 bytes, and a million kilobytes (that is, 1,024,000,000 bytes), or even just a billion bytes.
bytes, and a million kilobytes (that is, 1,024,000,000 bytes), or even just a billion bytes.
The Interstate (CIS) Standard GOST 8.417-2002 [1] (“Units of Value”) in “Appendix A” for the designation of a byte regulates the use of the Russian capital letter “B”. In addition, the tradition of using the SI prefixes with the name “byte” to indicate multipliers that are powers of two (1 Kbyte = 1024 bytes, 1 Mbyte = 1024 Kbytes, 1 Gbytes = 1024 Mbytes, etc.) is stated. "The capital" K "is used), and it is mentioned that this use of the SI prefixes is not correct.
Using a capital letter “B” to designate a byte meets the requirements of GOST and avoids confusion between abbreviations from bytes and bits. However, it should be noted that there is no abbreviation for “bits” in the standard, therefore the use of a record like “GB” as a synonym for “Gbit” is not allowed.
In the international standard IEC IEC 60027-2 2005 [2] , for applications in electrical and electronic fields, the following notation is recommended:
According to the recommendations of the Russian Language Institute named after V. V. Vinogradov of the Russian Academy of Sciences, bytes, like bits, must be inclined [ source not specified 1081 days ] .
In addition to the usual form of the genitive case (bits, bytes, kilobytes), there is a counting form, which is used in combination with numerals: 8 bytes, 16 kilobytes. The counting form is colloquial. Similarly, for example, with kilograms: the usual form of the genitive case is used *** if there is no numeral, and in combination with the numeral there may be options: 16 kilograms (stylistically neutral ordinary form) and 16 kilograms (colloquially countable form) [3 ] .
Bit (eng. Bi nary digi t is a binary number; also a pun: eng. Bit is a piece, a particle) is a unit of measure for the amount of information equal to one digit in a binary number system. It is denoted by GOST 8.417-2002. For the formation of multiple units is used with SI prefixes and binary prefixes.
In 1948, Claude Shannon proposed to use the word bit to denote the smallest unit of information in the article A Mathematical Theory of Communication .
Depending on the points of view, the bit can be determined in the following ways:
Two physical (in particular electronic) realizations of a bit (one binary digit) are possible:
In computing and data networks, usually values of 0 and 1 are transmitted by different voltage or current levels. For example, in ICs based on TTL, 0 is represented by a voltage in the range from +0 to +0.8 V , and 1 in the range from +2.4 to +5.0 V.
In computing, especially in documentation and standards, the word "bit" is often used to mean "binary digit." For example: the most significant bit is the most significant bit of the byte or word in question.
The analogue of a bit in quantum computers is a qubit (q-bit).
Bit (white-black) is one of the most famous pieces of information used.
Replacing the logarithm 2 with e, 3 or 10, respectively, leads to rarely used *** nat, thrit and hartdite units, respectively 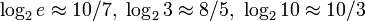 bit.
bit.
Trit - used in computer science, digital and computing.
1 trit ( trr ) is equal to the ternary logarithm of 3 possible states (codes) of one ternary digit
1 trit ( trr ) = log 3 (3 [ possible states (codes)])
1. One trit, as one ternary digit, can take three possible values (states, code): 0, 1 and 2.
2. One trit, as the ternary logarithm of 3 possible states (codes) of one ternary discharge, can take only one value equal to log 3 3 = 1.
Remedy of trit (trora) duality
If the value “1 ternary digit” is fixed with full names: the ternary digit and trinary digit , and the values “1 unit of storage capacity, 1 unit of data volume and 1 unit of amount of information” are assigned abbreviated names: tror and trit , then the duality (trit ) will disappear.
Capacity of one ternary discharge and volume "0", "1" and "2"
Empty ("0"), half-filled ("1") and fully filled ("2") 1 cubic capacity.
"2"> "1"> "0", and one trit, as a unit of measure for the storage capacity, corresponds to the largest possible volume, i.e. the value of the ternary discharge - "2". From this it follows that the value of the ternary discharge equal to "0" volume does not occupy, and the value of the ternary discharge equal to "1" occupies a volume equal to half of the largest.
It is obvious that the model in the figure on the right with the most approximation is described by a unary-coded ternary coding system (UnaryCodedTernary, UCT), in which: "0" - "", "1" - "1" and "2" - "11". In binary computers, the binary-encoded ternary coding system corresponds to a binary-coded unary-coded ternary coding system (BinaryCodedUnaryCodedTernary, BCUCT), in which: "0" - "00", "1" - "01" and "2" - "11".
Units of information for bits, nat, trit, and ban (decite)
With other bases of the logarithm, the logarithms of the 3 possible states (codes) are equal to:
log 2 (3 [possible states]) = ln 3 / ln 2 = 1.58 ... bits,
log e (3 [possible states]) = ln 3 = 1.09 ... Nata
log 3 (3 [possible states]) = 1 trit
...
log 10 (3 [possible states]) = 0.477 ... ban (Hartley, dita, decite)
...
|
|
This section of the article has not been written.
According to the plan of one of the participants in Wikipedia, this place should be a special section. |
Trit is a logarithmic unit of measure in information theory, the minimum integer unit of measure for the amount of information of sources with three equally probable messages. Entitropy of 1 trit has a source of information with three equally probable states. Simply put, by analogy with a bit that “reduces ignorance” about the object under study twice, trit “reduces ignorance” three times.
Used in information theory.
By analogy with the concept of "byte" there is the concept of "tray". For the first time the term was used in the computer of the tertiary logic Setun-70, where it was 6 tritas.
The analogue of trit in quantum computers is quutrit (q-trit).
The number of possible states of a memory device consisting of n elementary cells is determined in combinatorics, for positional coding it is equal to the number of arrangements with repetitions and is expressed by an exponential function:
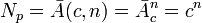 [possible states ] where
[possible states ] where
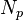 - the number of possible states (codes, values) during positional coding,
- the number of possible states (codes, values) during positional coding,
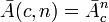 - the number of placements with repetitions,
- the number of placements with repetitions,
 - the number of possible states of one memory element, in SRAM - the number of trigger states, in DRAM - the number of recognizable voltage levels on the capacitor, in magnetic recording devices - the number of recognizable magnetization levels in one elementary recording section (one elementary recording section in recording devices magnetic tape, magnetic drums, magnetic disks - one recognizable elementary part of the track, in ferrite rings recording devices - one ferrite ring about),
- the number of possible states of one memory element, in SRAM - the number of trigger states, in DRAM - the number of recognizable voltage levels on the capacitor, in magnetic recording devices - the number of recognizable magnetization levels in one elementary recording section (one elementary recording section in recording devices magnetic tape, magnetic drums, magnetic disks - one recognizable elementary part of the track, in ferrite rings recording devices - one ferrite ring about),
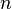 — количество тро ичных р азрядов ( трор ов, трит ов) (элементов запоминающего устройства), в SRAM — количество триггеров, в DRAM — количество конденсаторов, в устройствах с магнитной записью — количество элементарных участков записи (в устройствах записи на магнитную ленту, на магнитные барабаны, на магнитные диски — количество распознаваемых элементарных участков дорожки, в устройствах записи на ферритовые кольца — количество ферритовых колец).
— количество тро ичных р азрядов ( трор ов, трит ов) (элементов запоминающего устройства), в SRAM — количество триггеров, в DRAM — количество конденсаторов, в устройствах с магнитной записью — количество элементарных участков записи (в устройствах записи на магнитную ленту, на магнитные барабаны, на магнитные диски — количество распознаваемых элементарных участков дорожки, в устройствах записи на ферритовые кольца — количество ферритовых колец).
Так как прямая функция — зависимость количества состояний от количества разрядов — показательная, то обратная ей функция — зависимость количества разрядов от количества состояний — логарифмическая:
возьмём логарифм от обеих частей уравнения в предыдущем разделе, получим:
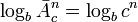 where
where
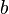 — основание логарифма,
— основание логарифма,
выведем показатель степени за знак логарифма, получим:
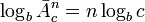
поменяем местами обе части уравнения и перенесём сомножитель при 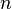 в правую часть в знаменатель дроби, получим:
в правую часть в знаменатель дроби, получим:
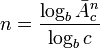 , [ тро ичных р азрядов ( трор ов, трит ов)],
, [ тро ичных р азрядов ( трор ов, трит ов)],
at 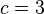 и применении троичного логарифма (
и применении троичного логарифма ( 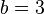 ) формула упрощается до:
) формула упрощается до:
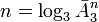 , [ тро ичных р азрядов ( трор ов, трит ов)].
, [ тро ичных р азрядов ( трор ов, трит ов)].
Цифровое запоминающее устройство представляет собой автомат с конечным числом состояний , причём возможен безусловный переход между любыми двумя произвольно выбранными состояниями .
|
Запоминающие устройства имеют одинаковую информационную ёмкость, если равны количества состояний , в которых они могут находиться. |
Если двоичное запоминающее устройство имеет 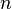 бит, то оно может принимать
бит, то оно может принимать
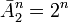 возможных состояний .
возможных состояний .
Аналогично, если троичное устройство имеет 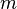 трит, то оно может принимать
трит, то оно может принимать
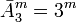 возможных состояний .
возможных состояний .
Частный случай 2.1
Приравнивая, получим, что ёмкость запоминающего устройства с 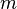 тритами равна
тритами равна 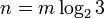 бит. Аналогично, ёмкость запоминающего устройства с
бит. Аналогично, ёмкость запоминающего устройства с 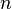 битами равна
битами равна 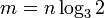 трит.
трит.
In this way:
6 тритов (длина машинного слова Сетуни) равны 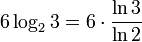 ≈ 9,51 бита. Следовательно, для кодирования машинного слова из 6 тритов требуется 10 битов.
≈ 9,51 бита. Следовательно, для кодирования машинного слова из 6 тритов требуется 10 битов.
1 байт равен 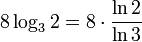 ≈ 5,047 трита. То есть, одного байта хватит для кодирования машинного слова длиной в 5 тритов.
≈ 5,047 трита. То есть, одного байта хватит для кодирования машинного слова длиной в 5 тритов.
1 килобайт равен 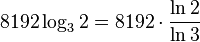 ≈ 5168,57 трита.
≈ 5168,57 трита.
Частный случай 2.2
1 трит равен 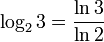 ≈ 1,585 бит.
≈ 1,585 бит.
Общий случай
В более общем случае отношение информационных ёмкостей двух запоминающих устройств с разными информационными ёмкостями элементов (разрядов) и с разным числом элементов (разрядов), выраженных в нелогарифмических единицах измерения ёмкости ЗУ и объёма информации - в количествах возможных состояний , равно:
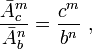 Where
Where
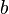 and
and  — количества возможных (вероятных) состояний элементарных ячеек сравниваемых запоминающих устройств,
— количества возможных (вероятных) состояний элементарных ячеек сравниваемых запоминающих устройств,
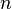 — количество элементарных устройств памяти запоминающего устойства в числителе,
— количество элементарных устройств памяти запоминающего устойства в числителе,
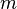 — количество элементарных устройств памяти запоминающего устройства в знаменателе.
— количество элементарных устройств памяти запоминающего устройства в знаменателе.
Отношение является функцией от четырёх аргументов, т.е. переменной.
Частный случай 1.1
Отношение информационных ёмкостей троичного ( 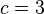 ) и двоичного (
) и двоичного ( 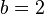 ) запоминающих устройств с разными информационными ёмкостями (
) запоминающих устройств с разными информационными ёмкостями ( 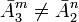 ), выраженными в нелогарифмических единицах измерения ёмкости ЗУ и объёма информации - в количествах возможных состояний , равно:
), выраженными в нелогарифмических единицах измерения ёмкости ЗУ и объёма информации - в количествах возможных состояний , равно:
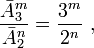 Where
Where
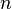 [битов] — количество элементарных двоичных устройств памяти (в двоичной SRAM - двоичных триггеров, в двоичной DRAM - конденсаторов с двумя распознаваемыми уровнями напряжений),
[битов] — количество элементарных двоичных устройств памяти (в двоичной SRAM - двоичных триггеров, в двоичной DRAM - конденсаторов с двумя распознаваемыми уровнями напряжений),
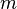 [тритов] — количество элементарных троичных устройств памяти (в троичной SRAM - троичных триггеров, в троичной DRAM - конденсаторов с тремя распознаваемыми уровнями напряжений).
[тритов] — количество элементарных троичных устройств памяти (в троичной SRAM - троичных триггеров, в троичной DRAM - конденсаторов с тремя распознаваемыми уровнями напряжений).
Отношение является функцией от двух аргументов, т.е. переменной.
Частный случай 1.2
При сравнении информационных ёмкостей троичного запоминающего устройства и двоичного запоминающего устройства с одинаковым количеством элементов ( 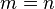 ), выраженных не в логарифмических единицах ёмкости носителя (объёма информации) (бит, трит), а в нелогарифмических единицах количества информации - в количествах возможных состояний (значений, кодов):
), выраженных не в логарифмических единицах ёмкости носителя (объёма информации) (бит, трит), а в нелогарифмических единицах количества информации - в количествах возможных состояний (значений, кодов):
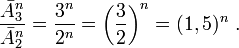
Отношение является функцией от одного аргумента, т.е. переменной, зависящей от числа разрядов - 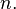
Частный случай 1.3
В ещё более частном случае, при сравнении информационных ёмкостей одного элемента троичного запоминающего устройства и одного элемента двоичного запоминающего устройства ( 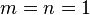 ) выраженных в нелогарифмических единицах информации - в количествах возможных состояний :
) выраженных в нелогарифмических единицах информации - в количествах возможных состояний :
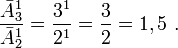
Отношение является константой (const), т.е. постоянной.
Следует отметить, что это не отношение логарифмических единиц измерения ёмкостей носителей и объёмов информации - трит а и бит а, а отношение ёмкостей носителей и объёмов информации, соответствующих трит у и бит у, выраженных в нелогарифмических единицах измерения ёмкостей носителей (ЗУ) и объёмов информации - в количествах возможных состояний . Those. не отношение 1 трит а к 1 бит у, а отношение количеств возможных состояний устройств, соответствующих 1 трит у и 1 бит у.
Частный случай 2.1
При одинаковых информационных ёмкостях двоичного устройства памяти и троичного устройства памяти ( 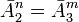 ), выраженных в нелогарифмических единицах измерения ёмкости ЗУ и объёма информации - в количествах возможных состояний :
), выраженных в нелогарифмических единицах измерения ёмкости ЗУ и объёма информации - в количествах возможных состояний :
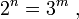
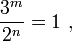
отношение является константой (const), т.е. постоянной, не зависящей от количества разрядов - 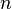 or
or 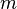 (при задании одного из двух количеств разрядов
(при задании одного из двух количеств разрядов 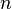 or
or 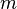 второе количество разрядов вычисляется).
второе количество разрядов вычисляется).
Возьмём натуральный логарифм от каждой из двух частей уравнения, при этом происходит переход от отношения количеств возможных состояний к натуральному логарифму отношения количеств возможных (вероятных) состояний:
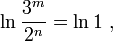
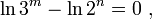
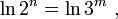
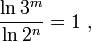
отметим, что произошёл переход от отношения объёмов (ёмкостей), выраженных в нелогарифмических единицах измерения ёмкости носителей и объёмов информации - в количествах возможных состояний , к отношению логарифмов объёмов (ёмкостей), т.е. к логарифмическим единицам измерения ёмкости носителей и объёмов информации - бит ам и трит ам,
выведем показатели степени за знак логарифма:
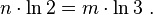
Из этого уравнения следуют две формулы:
1. для перевода логарифмической ёмкости троичного запоминающего устройства из тритов в биты:
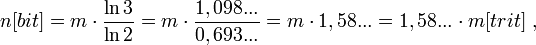
2. для перевода логарифмической ёмкости двоичного запоминающего устройства из битов в триты:
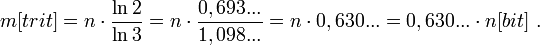
With a storage capacity of 6 trites (the length of the computer word Setun) 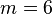 and:
and:
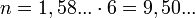 bits. Consequently, 10 bits are required to encode a word word of 6 trits.
bits. Consequently, 10 bits are required to encode a word word of 6 trits.
With a storage capacity of 9 trit 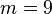 and:
and:
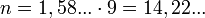 bits. Therefore, 16 bits = 2 Bytes are sufficient for coding a 9-ti machine word.
bits. Therefore, 16 bits = 2 Bytes are sufficient for coding a 9-ti machine word.
1 byte = 2 8 , i.e. n = 8 and:
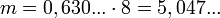 trit. That is, one byte is enough to encode a machine word 5 trits long.
trit. That is, one byte is enough to encode a machine word 5 trits long.
1 kilobyte is 2 13 , i.e. n = 13 and:
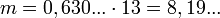 trit.
trit.
Special case 2.2
When comparing the information capacities of one element of the ternary memory device and one element of the binary memory device to the condition 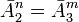 condition is added
condition is added 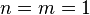 , with the equation:
, with the equation:
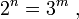 turns into an equation:
turns into an equation:
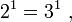 which is not true, i.e. under the imposed conditions, the special case equation 2 has no solution, which means that for comparing the information capacities of one element of the ternary storage device and one element of the binary storage device, the equation of the special case 2 is not suitable for this particular case and in this particular case
which is not true, i.e. under the imposed conditions, the special case equation 2 has no solution, which means that for comparing the information capacities of one element of the ternary storage device and one element of the binary storage device, the equation of the special case 2 is not suitable for this particular case and in this particular case
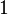 trit
trit 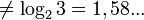 ≈ 1,585 bits.
≈ 1,585 bits.
In other words, since the equation in the particular case of 2.1 was derived under the condition 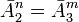 , and in this particular case
, and in this particular case 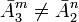 then it is not suitable for this case.
then it is not suitable for this case.
In this particular case, you need to use the equation from the special case 1.3.
Thus, the equation in the particular case 2.2 interpretation 1 is incorrect.
When throwing a three-sided ( b = 3) “chizh”, trinar entropy of the source (“chizh”)  with the original alphabet (numbers on the faces of a triangular "chizha")
with the original alphabet (numbers on the faces of a triangular "chizha") 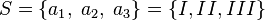 (a figure is read from the face lying on the ground) and a discrete uniform probability distribution (the section “chizh” is an equilateral triangle, the density of the material “chizh” is uniform throughout the entire volume of “chizh”)
(a figure is read from the face lying on the ground) and a discrete uniform probability distribution (the section “chizh” is an equilateral triangle, the density of the material “chizh” is uniform throughout the entire volume of “chizh”) 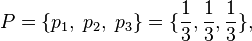 Where
Where 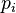 is a probability
is a probability 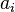 (
( 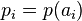 ) is equal to:
) is equal to:
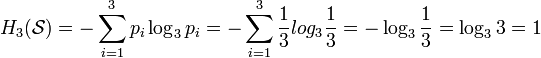 trit
trit
Trait is the minimum directly addressable unit of the main memory of Setun 70 of Brusentsov.
The trait is 6 tritas (almost 9.51 bits). In Setuni 70, it is interpreted as a significant integer in the range from -364 to 364.
The trait is large enough to encode, for example, the alphabet, which includes Russian and Latin upper and lower case letters, numbers, mathematical and service characters.
Spend a whole number of both 9-and 27-digit digits.
Cubit (q-bit, cubit, qubit; from quantum bit ) - a quantum discharge or the smallest element for storing information in a quantum computer.
Like a bit, a qubit allows two eigenstates, denoted by 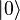 and
and 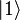 (designations of Dirac), but at the same time it can be in their superposition, that is, in the state
(designations of Dirac), but at the same time it can be in their superposition, that is, in the state 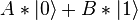 where
where 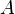 and
and 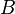 - complex numbers satisfying the condition
- complex numbers satisfying the condition 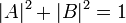 .
.
In any measurement of the qubit state, it randomly goes into one of its own states. The probabilities of transition to these states are equal respectively 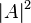 and
and 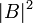 , that is, indirectly, by observing a multitude of qubits, we can still judge the initial state.
, that is, indirectly, by observing a multitude of qubits, we can still judge the initial state.
Qbits can be connected with each other, that is, an unobservable link can be imposed on them, which is expressed in the fact that with any change over one of several qubits, the others change consistently with it. In other words, a set of qubits entangled among themselves can be interpreted as a filled quantum register. Like a single qubit, the quantum register is much more informative than the classical register of bits. It can not only be in various combinations of its constituent bits, but also realize all sorts of subtle dependencies between them.
Despite the fact that we ourselves cannot directly observe the state of qubits and quantum registers in their entirety, they can exchange their state with each other and can transform it. Then there is the possibility to create a computer capable of parallel computing at the level of its physical device, and the only problem left is to read the final result of the calculations.
The word “qubit” was introduced into use by Ben Schumacher from Kenyon College (USA) in 1995, and AK Zvezdin in his article suggested a translation option “q-bit” [1] . Sometimes you can also find the name "quantum".
A generalization of the concept of a qubit is Kunit (Q-enk, kuenk; qudit), which can store more than two values in one bit (for example, qutrit English qutrit - 3, kukvadrit - 4, ..., kuenk - n) [2] .
Comments
To leave a comment
Informatics
Terms: Informatics