The calculation of electrical circuits using trigonometric functions is very complicated and cumbersome, therefore, when calculating electrical circuits of sinusoidal current, the mathematical apparatus of complex numbers is used.
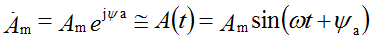
The modulus of the complex amplitude is equal to the amplitude of the sinusoidal magnitude, and the argument is its initial phase.
The concept of complex magnitudes and effective values of current, voltage, EMF, etc. is introduced.
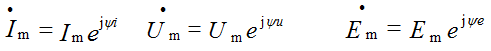
The complex effective values are proportional to the complex amplitudes and are written as:
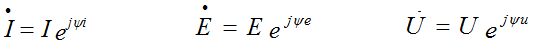
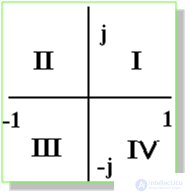
Sinusoidal electrical quantities, presented in a complex form, can be represented graphically. Complex vectors are built on the complex plane in the coordinate system with the axes +1 and + j, which denote the positive real and imaginary semiaxes. The length of the vector is proportional to the modulus of the effective values. The angular position of the vector is determined by the argument of the complex number. In this case, the positive angle is counted counterclockwise from the positive real semiaxis. The complex plane is divided into four quarters:
So, consider our trigonometric function A (t) represented as a complex value on the complex plane. It turns out that our function is represented as a vector rotating in the complex plane counterclockwise with a speed ω, as shown in Fig.1.
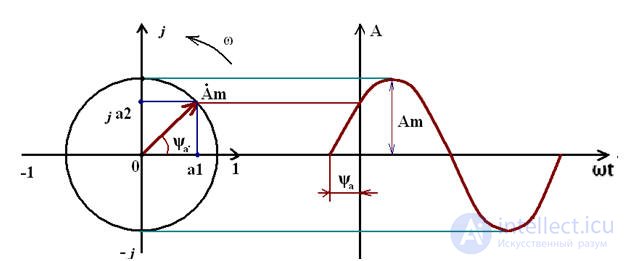
Pic.1
From Fig. 1 it is clear that a vector on the complex plane can be constructed in two ways, the first, knowing the size of the vector and the angle, and the second way, knowing the coordinates of the vector along the real and imaginary axes.
The first method is an exponential form of representing a complex number, i.e.
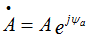
where is the complex value, A is the modulus of the complex number or the effective value of the value, ψa is the argument of the complex number
The second way is the algebraic form of representing a complex number:
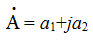
where а1 = Асоs ψа а2 = Аsin ψа
Rules of transition from one form to another.
Transition from exponential to algebraic form:
given
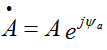
Euler's formula is used.
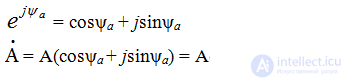
Transition from algebraic form to exponential form:
given
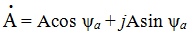
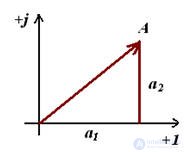
Fig. 2
It is clear from Fig. 2 that the vector forms a right triangle with the coordinate axis, so we use the Pythagorean theorem and find the size of the vector that is equal to the hypotenuse of the triangle
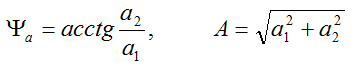
with special attention to the corner - the argument ψа of the module of a complex number:
if the vector is in the second and third quarters of the complex plane, then the resulting value of the argument must be added 180 ° or π.
If a1 = 0, then the complex number is called imaginary, the argument is ψа = ± 90 °
If a2 = 0, then the complex number is called real, ψа = 0, ± π
The simplest mathematical operations with complex numbers
The simplest mathematical operations such as addition, subtraction, multiplication and division are carried out with complex numbers as follows: addition and subtraction are conveniently carried out in algebraic form, and multiplication and division in exponential.
Single complexes 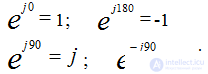 actions with j
actions with j 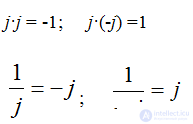
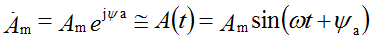
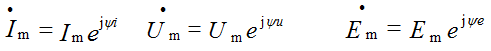
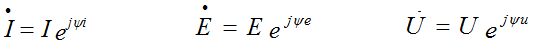


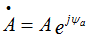
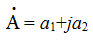
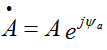
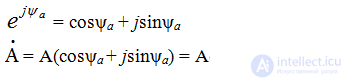
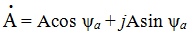

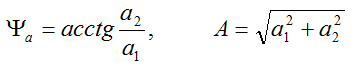
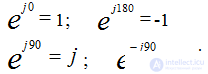
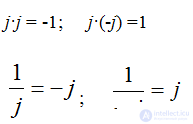
Comments
To leave a comment
Electrical Engineering, Circuit design
Terms: Electrical Engineering, Circuit design