Basic laws of magnetic circuits

Calculation of magnetic circuit

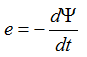
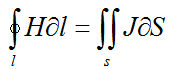
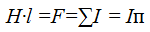
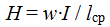
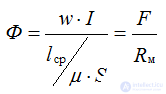
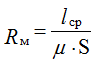
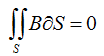
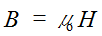
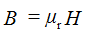
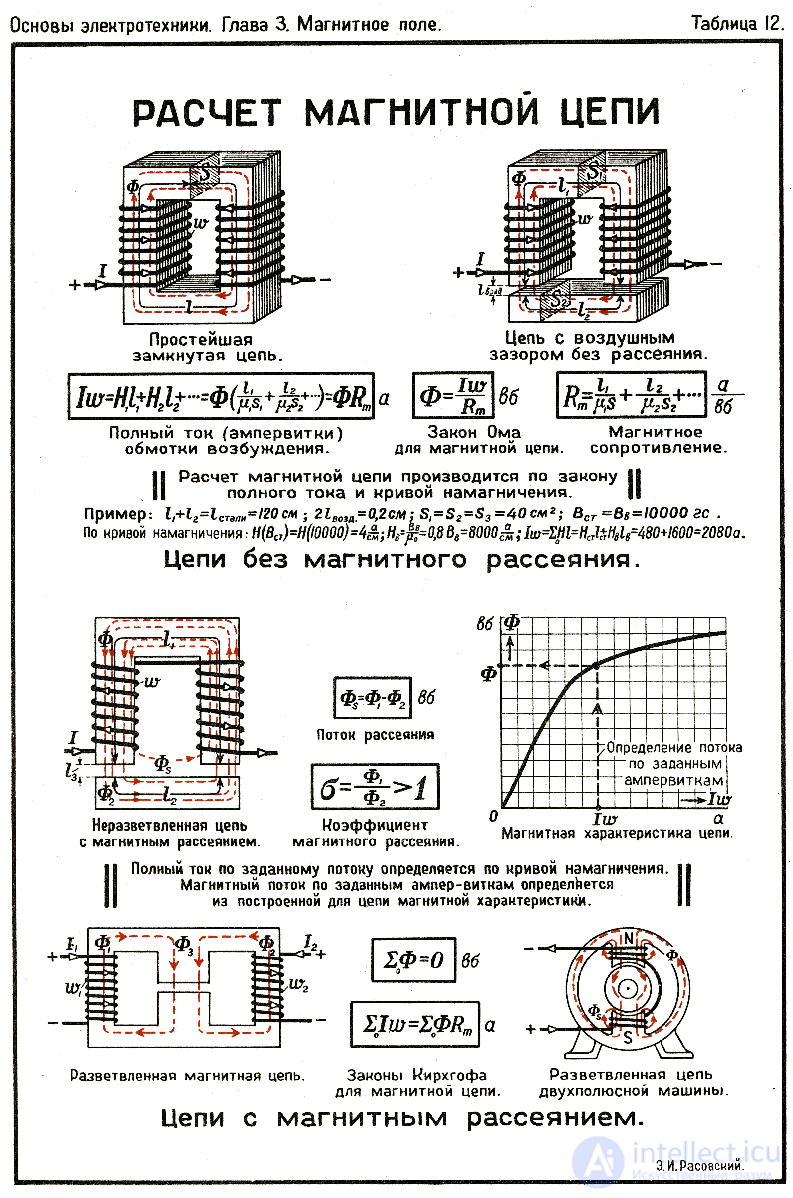
Magnetic circuits are calculated similarly to electrical ones, but instead of voltage, current and resistance, magnetic voltage (F), magnetic flux (Φ) and magnetic resistance (R) are used.

Basic equation:

F=ΦR

where

F=NI is the magnetomotive force (MMF) created by current I in a winding with N turns.
Φ is the magnetic flux in Webers.
R=μSl​ is the magnetic resistance, depending on the length of the magnetic circuit lll, the cross-sectional area S and the magnetic permeability μ.
For complex circuits, analogs of Kirchhoff's laws are used:

First law: the sum of magnetic fluxes in a node is zero.
Second law: the sum of magnetic voltages in a circuit is equal to the MMF.

Calculation of a branched magnetic circuit

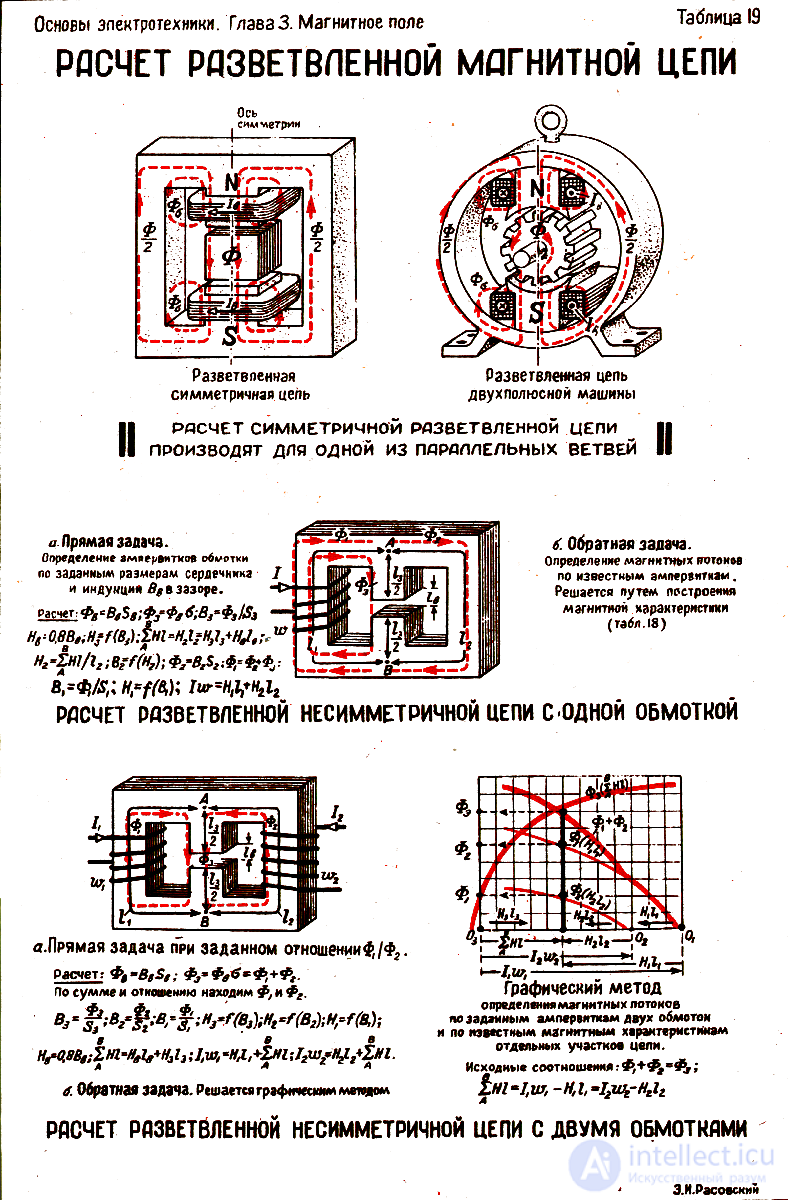
A branched magnetic circuit is an analog of a branched electric circuit, where magnetic fluxes are divided between different branches. The solution usually includes:

Determining the circuit topology (nodes, branches, loops).
Writing Kirchhoff's equations for magnetic circuits:
The sum of magnetic voltages (F) in a loop is zero.
The sum of fluxes (Φ) in a node is zero.
Calculating magnetic resistances (R=l/(μS)).
Solving a system of equations (e.g., using the nodal potential method or the loop current method).