Maxwell equations in differential form

Divergence (divergence) of the force vector F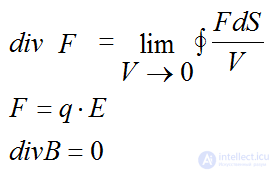



Any charge q being in an electric field of strength E is experiencing a force F.

Rotor (vortex of force vector F) lines of force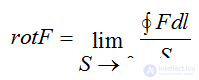



1st Maxwell's equation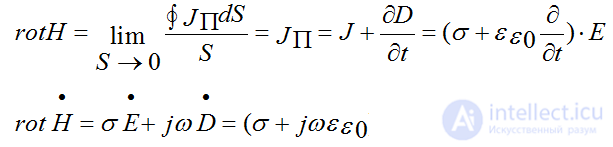



Differentiation is replaced by jω in the case of a simple harmonic signal

2nd Maxwell's equation the case of magnetic permeability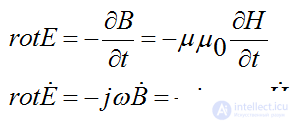



3rd equation Gauss equation for electrostatic field

The divergence of the electric displacement vector is equal to the electric charge density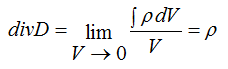



in case of constant permeability: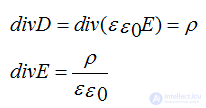



Relationship between vectors

J = σ • E - Ohm's law

D = ε0 • E + P

H = B / μ0 -M

Conductor with current divH = 0
Inside conductor rotH = J ≠ 0
There is no current in the outer region of the conductor. RotH = 0