A1 and A2 - are determined if the boundary conditions are known
U1 and I1 values at the beginning of the line (for X = 0)
If we choose arbitrarily U1 and I1, then we define it depending on them and on the line parameters by the resistance at the end of the Z2 line
at X = 0
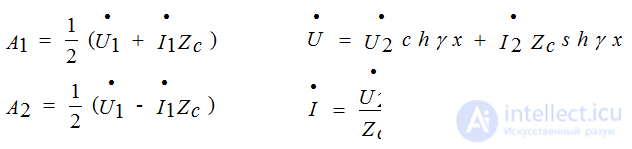
At a constant current ω = 0. There is no self-induction emf and bias currents between the wires. But there is an electric and magnetic field between the wires.
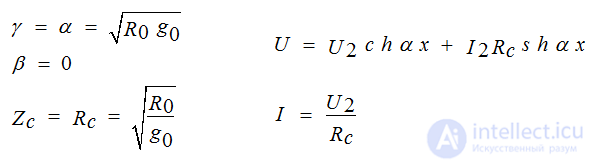
α - characterizes the attenuation of the amplitudes of the forward and reverse waves (Nep / km, dB / km)
β - characterizes the phase change of the wave depending on the x-point of the line (rad / km)
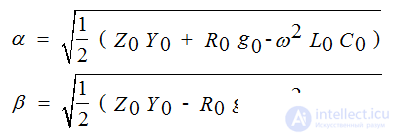
The resistance determines the currents of the forward and reverse waves at the corresponding voltages is called the wave Zc
The mean value of the Zc module for
overhead lines 300-400 ohms.
cable lines 50 ohm
In cable lines of strong current C0 is very large, L0 is very small, ε = 4-5, therefore the characteristic impedance is 6-8 times less than in overhead lines.
In lines with frequency ω = ∞
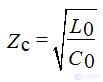
For air and cable lines g0, a negligible value, C0 is of great importance, therefore:
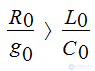
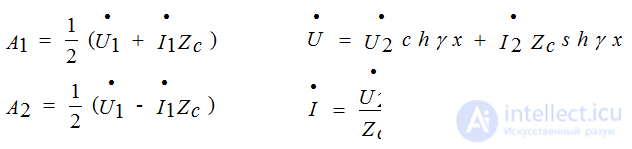
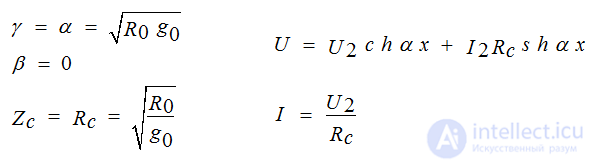
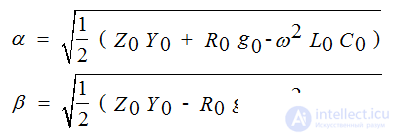
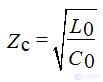
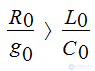
Comments
To leave a comment
Electrical Engineering, Circuit design
Terms: Electrical Engineering, Circuit design