Lecture
The coloring of graphs is practically applied (the formulation of the problem of different colorings will not be discussed here) for:
Probably, any particular type of coloring will be used in scheduling.
See also: Register allocation
A significant role in the speed of programs on the computer is played by the microprocessor accessing data. Namely, the processor can refer (we list the devices in decreasing order of speed and increase in volume) to:
Next, consider the optimization programs associated with the distribution of data in these devices.
The first [5] important works that laid the foundations for applying the graph coloring method in register allocation were [6] , [7] - the subsequent ones did not add anything revolutionary, their attention was focused on speeding up the algorithm, decreasing memory, new heuristics by definition the cost of pumping registers (we introduce the definition below) and the choice of registers for pumping; A review of these methods can be found in [8] .
Next, consider the method proposed in [7] .
Register allocation of a microprocessor is usually done at compile time.
A certain internal code ( IL , intermediate language , internal language ) is applied to the distribution procedure, which is designed for a virtual machine with an unlimited number of registers - we will call them virtual registers.
At the output, the procedures for accessing virtual registers are transferred either to real processor registers or, if the first one cannot be done due to the fact that all registers are already occupied, to real-time memory calls by introducing an additional code. This code is called the pumping code (English spillcode ), and the process itself - the pumping ( spilling ). Note that when accessing RAM, real registers are also sometimes used (for those processor commands that cannot take an address in memory as an argument).
For example, the number of general-purpose registers in most of the Intel processors corresponding to the architecture:
(However, not even all of them can be used in our procedure of register allocation, since they can already be occupied - but these are already subtle implementation issues.) The RAM can store a very large number of “pumped out” “registers” - restrictions on its size We will not consider.
Before performing the distribution procedure itself, you should do:
The register allocation algorithm itself consists of the following steps:
Practice shows that the algorithm converges fairly quickly.
The coloring of the graph is used in many well-known compilers, for example:
Processors capable of simultaneously and independently executing several instructions are becoming more widely used; they are said to be supported by teamwork parallelism ( Instruction-level parallelism , ILP ). Let's call them ILP processors. The class of ILP processors includes, among other things, processors with a very long command word - VLIW ( Very Large Instruction Word , among which are, in particular, many models of digital signal processing processors (DEPC). The most well-known commercially successful implementation of the concept of parallelism at the level of individual instructions is a family of microprocessors from Itanium by Intel. Also worth noting is the E2K architecture developed by the Russian company MCST.
For real-world use of high-performance ILP processors, high-level language compilers are needed that are capable of generating efficient code; including the optimization of the allocation of registers. The introduction of ILP requires a serious reworking of the Haitin method in terms of constructing an incompatibility graph; [5] proposed a modified version.
An algorithm was also proposed for the distribution of frequently used areas of code in the cache [10] - so-called. English cache line coloring .
The incompatibility graph here is: vertices are some “blocks” of code (for example, you can take procedures), edges exist when another is called from one “block”. As you can see, we concentrate on the so-called. first-generation cache conflicts - between the “block” and its caller / callee. But it is worth noting that the coloring problem is not solved by general-purpose algorithms, but by a special heuristic, which, moreover, gives a solution that satisfies certain additional conditions.
The advantage of this method is that it takes into account cache sizes, cache lines, code “blocks”, and cache associativity. The method is successfully combined with other optimizations and inline-functions [10] [11] . It should be noted that it can be implemented by the optimizer - but not by the optimizer of the compiler, but by the optimizer of the linker.
(Eng. Spectrum management , Eng. frequency allocation )
A good work classifying such problems and systematically setting out their solutions is [12] .
The term “frequency allocation” unites different types of tasks, which often have different goals and models. These tasks include:
The common thing between tasks is that they all produce an optimal distribution of a limited set of radio spectrum resources among users, the number of which is constantly growing in modern conditions.
Two main areas of optimization here:
In the course of considering suitable models, in [12] , problems arise not much more complicated than T-coloring (English T-coloring ) of a multigraph, list T-coloring (English set T-coloring ).
As an example of work on a real cellular network, the results of which were further applied by the operator in their practical activities - [13] (Conducted by the operator E-Plus ((eng.) En: E-Plus) - the 3rd largest in Germany (2010 )).
To summarize, we will present the problem as follows: objects are certain calculations between which it is necessary to divide the computing resources (processors, computers ...) that can work in parallel with each other. Some calculations can be performed in parallel to each other, some - no. Accordingly, the vertex coloring of the incompatibility graph of the calculations is the desired distribution.
Let us give the following examples of numerical methods that can be parallelized in this way:
Cholesky decomposition for the conjugate gradient method with predestination [edit]
See also: en: Conjugate gradient method # The preconditioned conjugate gradient method
[14] This method is one of the best iterative methods for solving systems of linear algebraic equations (SLAE) with large, sparse, symmetric, positively defined matrices.
Gauss – Seidel method as applied to sparse matrices [edit]
The same iterative method for solving SLAU.
This, in turn, is good, for example, for calculating power distribution grids: such networks can be represented by graphs whose vertices are consumers and sources of electricity, and the edges are power lines; further, a SLAE is constructed, in the matrix of which the diagonal elements correspond to the nodes of the aforementioned graph, and non-zero non-diagonal elements correspond to edges. [15]
Also, the method can be so-called. smoother (English iterative smoother ) for multigrid finite element problem solving methods. (English multigrid methods of finite element problems ). Optimization of the Gauss – Seidel method used in smoothing using the so-called English sparse tiling for such a case of its use is considered in [16] .
Methods using adaptive refined grids [edit]
(English Adaptive mesh refinement )
[17] They, in turn, are useful in solving partial differential equations (DPEs). The clarification principle here is this: in places where the greatest local error is expected — where the solution changes most rapidly, the grid density is chosen to be greater.
Coordinate relaxation method [edit]
(eng. method of coordinate relaxation )
[18] It is successfully used in finding the extremal eigenvalues of very large sparse symmetric matrices. Sometimes so large that it is more practical to generate them on the fly than to store them in memory. Such problems often arise in quantum mechanics.
Predefinition by incomplete LU decomposition [edit]
( Preconditioning by ILU, Incomplete LU-factorization )
To solve the slau using the Krylov subspaces. [nineteen]
Calculation of matrices of derivatives (Jacobians and Hessians) in the case when they are sparse, can be seriously accelerated by coloring the graphs. There is a project "Graph Coloring for Computer Derivatives", site - [www 3] . The site contains publications on the topic, as well as - a software package, in which the project participants have drawn up their achievements. For an introduction to the subject, you can see one of the presentations related to the project - [20] .
For a simple case when the “compaction” of a derivative is limited to a decrease in the number of columns, we give an algorithm:
Input : function from vector - 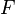
Output : derivative 1. Investigate the structure of the sparseness of the derivative 2. Make a matrix 3. Calculate the compacted values 4. And now, restore the values |
Coloring graph here - in the calculation 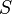 . In simple cases, it is necessary to calculate the usual vertex (born distance-1 ); distance-2 coloring (which, including reduced to square -distance distance-1 coloring); in more complex, small additional restrictions are required:
. In simple cases, it is necessary to calculate the usual vertex (born distance-1 ); distance-2 coloring (which, including reduced to square -distance distance-1 coloring); in more complex, small additional restrictions are required:
Within the framework of the above project, calculations were carried out for technical production problems:
Digital watermarking technology (English digital watermarking ) allows along with data (whether it be media files, executable files, and others) to transmit some hidden message ("watermark", Watermark ). Such a hidden message can be used in copyright protection to identify the owner of the data.
This is important, for example, to determine the source of their distribution in an illegal manner. Or to confirm the rights to the data, for example - software systems on a chip ( system-on-chip ).
The message can be encoded including in the column. One of these techniques was proposed by Qu and Potkonjak (therefore, it is sometimes called the QP algorithm) in [21] .
It consists of this: let's say we have a graph G, the coloring of which is used in the program - moreover, it is used in such a way that it is permissible to change the contents of the graph with a slight increase in its chromatic number. What is important, one of such examples is the incompatibility graph of the register of the processor, which was mentioned above, which means that we will be able to encode the message in a software product using the distribution of registers.
You can extract it by comparing the resulting graph with the original one; there are also ways to ascertain whether a message was encoded in the graph without using the original one — the extraction is described in more detail, for example, in [22] .
The development and refinement of the thoughts of Qu and Potkonjak , attempts to improve the algorithm occur in [23] , [24] , [22] .
Note that in [23] , [24] there are references to the SandMark software package, in which algorithms of this kind are executed; available for download at [www 4] .
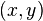 and
and 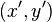 hold if and only if:
hold if and only if:
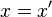 , or,
, or,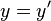 , or,
, or,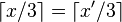 and
and 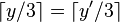 .
.
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.