Lecture
The factorial of the number n (lat. Factorialis - acting, producing, multiplying; denoted n !, Pronounced en factorial ) - the product of all natural numbers from 1 to n inclusive:

For example:
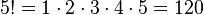 .
.
By agreement: 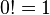 . This equality also holds naturally:
. This equality also holds naturally:
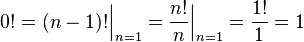
Factorial is defined only for non-negative integers.
The sequence of factorials of non-negative integers begins like this:
1, 1, 2, 6, 24, 120, 720, 5040, 40 320, 362 880, 3 628 800, 39 916 800, 479 001 600, 6 227 020 800, 87 178 291 200, 1 307 674 368 000, 20 922 789 888 000, 355 687 428 096 000, 6 402 373 705 728 000, 121 645 100 408 832 000, 2 432 902 008 176 640 000, ... [1]
Factorials are often used in combinatorics, number theory and functional analysis.
Factorial is an extremely fast growing feature. It grows faster than a polynomial of any degree, and faster than an exponential function (but slower than a double exponential function 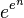 ).
).
Properties
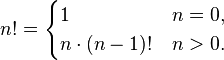
In combinatorics, the factorial of a natural number n is interpreted as the number of permutations (orderings) of a set of n elements. For example, for the set { A , B , C , D } of 4 elements, there are 4! = 24 permutations:
ABCD BACD CABD DABC ABDC BADC CADB DACB ACBD BCAD CBAD DBAC ACDB BCDA CBDA DBCA ADBC BDAC CDAB DCAB ADCB BDCA CDBA DCBA
The combinatorial interpretation of factorial justifies the identity 0! = 1, since the empty set is ordered in a unique way.
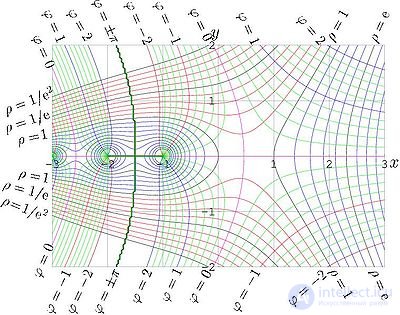
The amplitude and factorial phase of the complex argument.
Factorial is associated with the gamma function of an integer argument as follows:
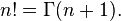
Thus, the gamma function is considered as a generalization of factorial for positive real numbers.
By analytic continuation, it is also extended to the entire complex plane, excluding singular points with 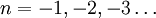 .
.
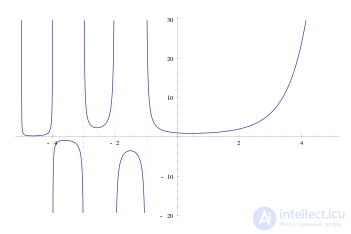
Pi-function, defined for all real numbers, except negative integers, and the same for natural values of the argument with the factorial.
A more direct generalization of factorial to a set of real (and complex) numbers is the pi function, defined as
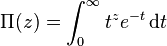 .
.
Insofar as 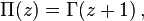 then the pi function of a natural number coincides with its factorial:
then the pi function of a natural number coincides with its factorial: 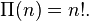 As a factorial, the pi function satisfies the recursive relation
As a factorial, the pi function satisfies the recursive relation 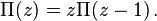
Main article: Stirling formula
Stirling's formula is an asymptotic formula for calculating factorial:
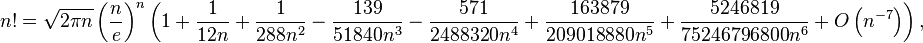
see O-large [2] .
In many cases, for the approximate value of factorial, it suffices to consider only the main member of the Stirling formula:
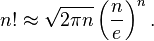
In this case, it can be argued that
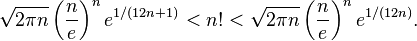
The Stirling formula allows to obtain approximate values of factorials of large numbers without directly multiplying the sequence of natural numbers. So, using the Stirling formula, it is easy to calculate that
Every prime number p is in the decomposition n ! by prime factors to the degree
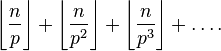
In this way,
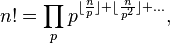
where the product is taken over all prime numbers. It is easy to see that for every simple p greater than n, the corresponding factor in the product is 1, and therefore the product can be taken only for simple p , not exceeding n .
For non-negative integer n :
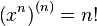
For example:
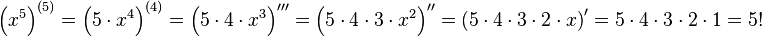
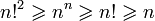
The double factorial of n is denoted by n !! and is defined as the product of all natural numbers in the interval [1, n ] having the same parity as n .
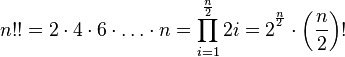
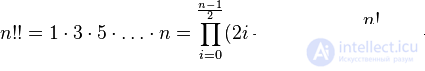
The relationship between the double factorials of two adjacent non-negative integers and the usual factorial of one of them.
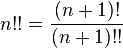
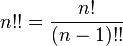
Derivation formulas
By replacing 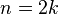 for even n and
for even n and 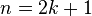 for odd n respectively, where
for odd n respectively, where 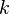 - nonnegative integer, we get:
- nonnegative integer, we get:
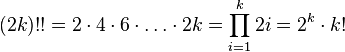
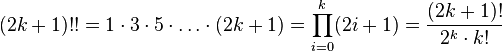
By agreement: 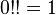 . This equality also holds naturally:
. This equality also holds naturally:
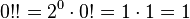
The double factorial, as well as the usual factorial, is defined only for non-negative integers.
The sequence of values of n !! starts like this:
1, 1, 2, 3, 8, 15, 48, 105, 384, 945, 3840, 10 395, 46 080, 135 135, 645 120, 2 027 025, 10 321 920, 34 459 425, 185 794 560, 654 729 075, 3 715 891 200, 13 749 310 575, 81 749 606 400, 316 234 143 225, 1 961 990 553 600, 7 905 853 580 625, 51 011 754 393 600, ... [3] .
The m- factorial of n is denoted by 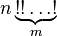 and is defined as follows. Let the number n be represented as
and is defined as follows. Let the number n be represented as 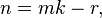 Where
Where 
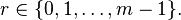 Then [4]
Then [4]
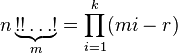
Normal and double factorials are special cases of m -fold factorial for m = 1 and m = 2, respectively.
Multiple factorial is associated with the gamma function as follows [5] :
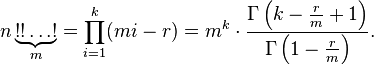
Decreasing factoria
Decreasing factorial is an expression
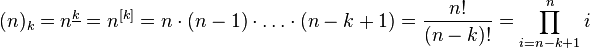 .
.
For example:
n = 7; k = 4
( n - k ) + 1 = 4,
3 k = 7 • 6 • 5 • 4 = 840.
The decreasing factorial gives the number of allocations from n by k .
Increasing factorial
Increasing factorial is the expression
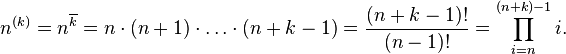
The “Primeor” request is redirected here. This topic needs a separate article.
A primeor or primorial (born primorial ) of the number n is denoted p n # and is defined as the product of n first prime numbers. For example,
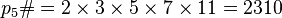 .
.
Sometimes primaries call number 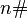 , defined as the product of all primes not exceeding a given n.
, defined as the product of all primes not exceeding a given n.
The sequence of primoryals (including 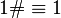 ) starts like this:
) starts like this:
1, 2, 6, 30, 210, 2310, 30 030, 510 510, 9 699 690, 223 092 870, 6 469 693 230, 200 560 490 130, 7 420 738 134 810, 304 250 263 527 210, 13 082 761 331 670 030, 614 889 782 588 491 410, 32 589 158 477 190 044 730, 1 922 760 350 154 212 639 070, ... [6] .
Neil Sloan and Simon Pumpoff ( English ) in 1995 identified the superfactory as a product of the first n factorials. According to this definition, the superfactory of four is

(since there is no established designation, functional is used).
Generally
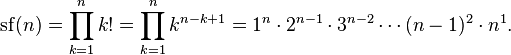
The sequence of superfactory numbers 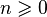 starts like this:
starts like this:
1, 1, 2, 12, 288, 34 560, 24 883 200, ... [7] .
The idea was generalized in 2000 by Henry Bottomley ( Eng. ), Which led to hyperfactorials (English Superduperfactorial ), which are the product of the first n superfactors. The sequence of hyperfactorials of numbers 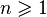 starts like this:
starts like this:
1, 1, 2, 24, 6912, 238 878 720, 5 944 066 965 504 000, 745 453 331 864 786 829 312 000 000, 3 769 447 945 987 085 350 501 386 572 267 520 000 000 000, 6 916 686 207,999 802,072,984,424 331,678,589,933,649,915,805,696,000,000,000,000 ... [8] .
Continuing recurrently, one can define the factorial of a multiple level , or m- level factorial of n , as the product of the first n ( m −1) -level factorials, that is,
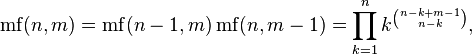
Where 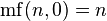 for
for 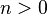 and
and 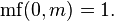
Main article: Subfactorial
Subfactorial ! n is defined as the number of disorder of order n , that is, permutations of an n -element set without fixed points.
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.