Lecture
If the set of vertices of a graph is finite, then it is called a finite graph. The finite graph G = (V, E), containing p vertices and q edges, is called a (p, q) -graph.
Let V == {v1, v2, ..., vp} and E == {е1, е2, ..., eq} be the sets of vertices and edges of an (p, q) -graph, respectively. Each edge ek <E connects a pair of vertices vi, vj <V, which are its ends (boundary vertices). For oriented edge (arc). distinguish the initial vertex from which the arc originates, and the final vertex at which the arc enters. An edge whose boundary vertices are the same vertex is called a loop. Edges with identical boundary vertices are parallel and are called multiple. In the general case, a graph can contain isolated vertices that are not the ends of edges and are not connected with each other or with other vertices.
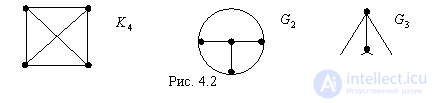
The number of edges associated with vertex vi (the loop is counted twice) is called the degree of the vertex and is denoted by (vi) or deg (vi). So, for the graph in Figure 2.2, a (v1) == 1, (v2) = 4, etc. Obviously, the degree of an isolated vertex is zero (((v4) = 0). The vertex of the degree of unity is called the terminal or hanging vertex ((v1) = 1). It is easy to show that in any graph the sum of the degrees of all vertices is equal to twice the number of edges, and the number of vertices of odd degree is always even. In the digraph, positive + (vi) and negative - (vi) degrees of vertices are distinguished, which are equal, respectively, to the number of outgoing from vi and entering into vi arcs. For example, for the vertex d of a digraph (see Figure 2.1, a) we have + (d) = 2 and - (d) = 3. Obviously, the sums of positive and negative powers of all vertices of the digraph are equal to each other and are also equal to the number of all arcs.
A graph without loops and multiple edges is called simple or ordinary. A graph without loops but with multiple edges is called a multigraph. The most common case of a graph when loops and multiple edges are allowed is called a pseudograph. So, the graph in Figure 2.2, b is a multigraph, and in Figure 2.2, a is a pseudograph. If a graph has no edges, then all its vertices are isolated, and it is called empty or a null graph. A simple graph in which any two vertices are connected by an edge is called complete (in Figure 2.2, b is an example of a complete graph with six vertices). If the set of vertices V of a simple graph admits such a partition into two disjoint subsets V1 and V2 that there are no edges connecting the vertices of the same subset, then it is called a bipartite or bi-graph (Figure 2.2, c). A directed graph is considered simple if it does not have strictly parallel arcs and loops.
A graph whose degrees of all vertices are the same and equal to r is called homogeneous (regular) rth degree. A complete graph with n vertices is always homogeneous of degree n2 - 1, and an empty graph is homogeneous of degree 0. A graph of third degree is called cubic. It has a number of interesting properties and, in particular, always has an even number of vertices.
If the graph has no edges (i.e. 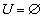 ), then all its vertices are isolated, and it is called an empty or null -graph .
), then all its vertices are isolated, and it is called an empty or null -graph .
A simple undirected graph in which any two vertices are connected by an edge is called complete . A full graph with n vertices is denoted by Kn (Fig. 4.2, graph K4). A graph of order n without edges is called empty and is denoted On .
The graph is called trivial. You can extend the complete graph to a complete graph with loops by adding a loop at each vertex (Fig.4.6).
 In a directed full graph, there are pairs of edges, one in each direction, connecting any two different vertices.
In a directed full graph, there are pairs of edges, one in each direction, connecting any two different vertices.
The tournament is called digraph, any pair of vertices of which is connected only by one arc. A tournament differs from a full directed graph in that it does not have oppositely directed arcs.
A graph is called homogeneous (regular) of degree k if the degrees of all its vertices are the same and equal to k. A homogeneous graph of degree 1 is called a matching . Examples of homogeneous graphs are the graphs formed by the vertices and edges of the five first regular polyhedrons (or, as they are called, Platonic solids ): tetrahedron and cube (degree 3), octahedron (degree 4), dodecahedron (degree 3), icosahedron (degree 5 ). The graph of the third degree is called cubic , it has a number of interesting properties and, in particular, it always has an even number of vertices. Three cubic graphs are depicted in Figure 4.2.
From the above formula, connecting the number of links of the graph m with the powers of its vertices, for the case of a uniform graph of degree k (all 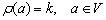 ), we get:
), we get:
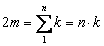 .
.
We remind that - 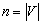 the number of vertices of the graph. Therefore, if an odd number, then n must be even, and, therefore, for any homogeneous graph of odd degree (and cubic too) there is always an even number of vertices.
the number of vertices of the graph. Therefore, if an odd number, then n must be even, and, therefore, for any homogeneous graph of odd degree (and cubic too) there is always an even number of vertices.
An orgraph is called homogeneous of degree k if the half-degrees of all its vertices are the same and equal: ==. In this case
.
Here, as before, n and m are the number of vertices and arcs of the graph.
If the set of vertices of a simple graph can be divided into two disjoint subsets (parts) V1, V2 ( 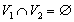 ) and at the same time there are no edges connecting the vertices of the same subset, then such a graph is called bipartite (otherwise, a biggraph ). Full bipartite (each vertex from V1 is connected to each vertex from V2). denoted by symbol
) and at the same time there are no edges connecting the vertices of the same subset, then such a graph is called bipartite (otherwise, a biggraph ). Full bipartite (each vertex from V1 is connected to each vertex from V2). denoted by symbol 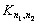 Where
Where 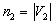 ,
, 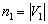 . Graph
. Graph 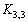 depicted in Figure 4.13.
depicted in Figure 4.13.

Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.