Lecture

Correct coloring of graph vertices by the smallest set of colors - three.
In graph theory, the coloring of graphs is a special case of graph marking [en] . When coloring, the elements of the graph correspond to the labels, taking into account certain restrictions; These labels are traditionally called “flowers.” In the simplest case, such a method of coloring the vertices of a graph, in which different colors correspond to any two adjacent vertices, is called vertex coloring . Similarly, edge coloring assigns a color to each edge so that any two adjacent edges have different colors. [1] Finally, the coloring of areas of a planar graph designates the color of each area, so that every two areas that have a common border cannot have the same color.
The coloring of the vertices is the main task of coloring the graphs; all other tasks in this area can be reduced to it. For example, the coloring of the edges of a graph is the coloring of the vertices of its edge graph, and the coloring of the areas of a planar graph is the coloring of the vertices of its dual graph. [1] However, other problems coloring graphs are often posed and solved in the original formulation. The reason for this is partly because it gives a better idea of what is happening and is more revealing, and partly because it is more convenient to solve some problems in this way (for example, coloring of edges).
Coloring graphs is used in many practical areas, not only in theoretical problems. In addition to the classic types of problems, various restrictions may also be imposed on the graph, on the method of assigning colors or on the colors themselves. This method, for example, is used in the popular Sudoku puzzle. Active research is still underway in this area.
The first results were obtained for flat graphs in the problem of coloring maps. Trying to color the map of the districts of England, Francis Guthrie formulated the four colors problem, noting that four colors are enough to color the map so that any two adjacent regions have different colors. His brother referred the question to his math teacher, Augustus de Morgan, who mentioned it in his letter to William Hamilton in 1852. Arthur Cayley raised this issue at a meeting in London in 1878. In the same year, Tate proposed the first solution to this problem. He reduced the coloring of the vertices of the original graph to the edge coloring of the dual graph and suggested that this problem always has a solution. [2] In 1880, Alfred Kempe [en] published an article stating that he was able to establish the result, and the problem of four colors was considered solved for a decade. For this achievement, Kempe was elected a member of the Royal Society of London and later - President of the London Mathematical Society. [3]
In 1890, Hivoud [ru] found a mistake in proving Kempe. In the same article, he proved the five-color theorem, showing that any flat map can be painted in no more than five colors. However, he relied on the ideas of Kempe. In the next century, a large number of theories were developed in an attempt to reduce the minimum number of colors. The four-color theorem was finally proved in 1977 by scientists Kenneth Appel and Wolfgang Hacken using computer brute force. The idea of the proof was largely based on the ideas of Hewood and Kempe and ignored most of the intermediate studies. [4] The proof of the four-color theorem is one of the first proofs in which a computer was used.
In 1912, George David Birkhof proposed to use the chromatic polynomial, which is an important part in algebraic graph theory, to study coloring problems. The chromatic polynomial was subsequently compiled by William Tat (Tatta polynomial). Kempe in 1879 already paid attention to the general case when the graph was not flat. [5] Many results of generalizations of coloring of flat graphs on surfaces of higher orders appeared at the beginning of the 20th century.
In 1960, Claude Berge [ru] formulated a hypothesis about perfect graphs, motivated by the notion of information theorems, namely the zero error of the capacity of the graph [6] , presented by Shannon. The statement remained unconfirmed for 40 years, until it was proved as the famous rigorous theorem on perfect graphs [en] by mathematicians Chudnovskaya [en] , Robertson [en] , Seymour [en] and Thomas [en] in 2002.
The coloring of graphs as an algorithmic problem began to be studied since the 1970s: the definition of the chromatic number is among the 21 NP-complete Karp problems (1972). And at about the same time, various algorithms were developed based on a search with a return and recursive deletion and Zykov contraction. [7] Since 1981, the coloring of the graph has been used to allocate registers in compilers. [eight]

This graph can be colored in 3 colors in 12 ways.
When they talk about coloring graphs, they almost always mean by this the coloring of their vertices, that is, the assignment of color labels to the vertices of the graph so that any two vertices that have a common edge have different colors. Since the graphs in which there are loops can not be colored in this way, they are not the subject of discussion.
The terminology in which labels are called colors comes from the coloring of political maps. Labels such as red or blue are used only when the number of colors is small, but usually it is assumed that the labels are integers {\ \ {1,2,3, ... \}} .
Coloring with {\ k} colors called {\ k}
painting . The smallest number of colors needed to color the graph {\ G}
, is called its chromatic number and is often written as {\ \ chi (G)}
. Sometimes used {\ \ gamma (G)}
since {\ \ chi (G)}
denotes the Euler characteristic. A subset of the vertices in one color is called a color class , each such class forms an independent set. Thus, {\ k}
-coloring is the same as dividing vertices into {\ k}
independent sets. [one]
Chromatic polynomial is a function {\ P (G, t)} which counts the number of t- colorings of the graph {\ G}
. The name implies that for given {\ G}
this function is a polynomial dependent on t . This fact was discovered by Birkhoff and Lewis while trying to prove the hypothesis of four colors. [9]
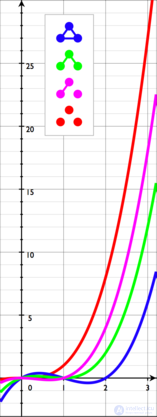
All non-isomorphic graphs from 3 vertices and their chromatic polynomials. The empty graph E 3 (red) allows coloring in one color, the others are not. A green graph can be colored in 3 colors in 12 ways.
For example, the graph in the image on the right can be colored in 12 ways using 3 colors. Two colors it can not be painted in principle. Using 4 colors, we get 24 + 4 * 12 = 72 coloring options: when using all 4 colors, there are 4! = 24 correct ways ( each assignment of 4 colors for any graph of 4 vertices is correct); and for every 3 colors of these 4 there are 12 coloring methods. Then, for the graph in the example, the table of numbers of correct colorings will start like this:
| Available number of colors | one | 2 | 3 | four | ... |
| The number of ways to paint | 0 | 0 | 12 | 72 | ... |
For the graph in the example, {\ P (G, t) = t (t-1) ^ {2} (t-2)} and of course, {\ P (G, 4) = 72}
.
The chromatic polynomial contains at least as much colorization information {\ G} how much and chromatic number. In fact, {\ \ chi}
- the smallest positive integer that is not the root of the chromatic polynomial.
{\ \ chi (G) = \ min \ {t \, \ colon \, P (G, t)> 0 \}.}
| Triangular {\ K_ {3}} |
{\ t (t-1) (t-2)} |
| Complete graph {\ K_ {n}} |
{\ t (t-1) (t-2) \ cdots (t- (n-1))} |
| Tree with {\ n} |
{\ t (t-1) ^ {n}} |
| Cycle {\ C_ {n}} |
{\ (t-1) ^ {n} + (- 1) ^ {n} (t-1)} |
| Count Petersen | {\ t (t-1) (t-2) (t ^ {7} -12t ^ {6} + 67t ^ {5} -230t ^ {4} + 529t ^ {3} -814t ^ {2} + 775t-352)} |
The edge coloring of a graph implies the assignment of colors to edges so that no two edges of the same color belong to the same vertex. This task is equivalent to dividing the set of faces into sets of independent faces. The smallest number of colors required for the line coloring of the graph {\ G} - this is its chromatic index , or an edge chromatic number , {\ \ chi '(G)}
.
Total coloring is one of the types of coloring of the vertices and edges of the graph. Under it implies such an assignment of colors that neither adjacent vertices, nor adjacent edges, nor vertices and edges that connect them, do not have the same color. Full chromatic number {\ \ chi '' (G)} graph {\ G}
- This is the smallest number of colors needed for any full coloring.
{\ P (G, t) = 1}
{\ P (G, t) = P (H, t) P (K, t)}
{\ P (G, t) = 0}
{\ 1 \ leq \ chi (G) \ leq n. \,}
{\ \ chi (G) (\ chi (G) -1) \ leq 2m. \,}
{\ \ chi (G) = max \ {\ chi (H), \ chi (K) \}}
{\ \ chi (G) \ geq \ omega (G). \,}
For interval graphs, this restriction is exact.
{{ G} graph is bipartite if and only if it does not contain cycles of odd length. [ten]
{\ \ chi (G) \ leq \ Delta (G) +1. \,}
{\ \ chi (G) \ leq \ Delta (G)} for a connected, simple graph {\ G}
if {\ G}
is neither a complete graph, nor a cycle graph.
Mychelsky theorem (Alexander Zykov 1949, Jan Mychelsky, 1955): There are graphs without triangles with arbitrarily large chromatic numbers.
Erdös theorem : There are graphs with arbitrarily large girth and chromatic number. [eleven]
{\ \ chi '(G) = \ chi (L (G)). \,}
Koenig theorem: {\ \ chi '(G) = \ Delta (G)} if {\ G}
- dicotyledonous.
Vizing's Theorem: Graph with the maximum degree of the vertex {\ \ Delta} has an edge chromatic number {\ \ Delta}
or {\ \ Delta +1}
.
The chromatic number of the plane in which the two points are adjacent if the unit distance between them is unknown. It can be 4, 5, 6, or 7. Other open questions about the chromatic number of graphs include the Hadwiger hypothesis, stating that any graph with chromatic number k has a complete graph of k vertices, like its minor, Erdрдos – Faber hypothesis –Lovasa [en] , which limits the chromatic number of complete graphs that have exactly one common vertex for each pair of graphs, and the Albertson hypothesis [en] that among the k -chromatic graphs, those that have the least number of intersections are complete.
When Birkov and Lewis introduced the chromatic polynomial in their attempt to solve the four-color theorem, they argued that for flat graphs {\ G}, the {\ P (G, t)} polynomial
does not have zeros in the {\ [4, \ infty)}
.Although it is known that such a chromatic polynomial does not have zeros in the area {\ [5, \ infty)}
, and that {\ P (G, 4) \ neq 0}
, their assertion remains unproved. It also remains an open question how to distinguish graphs with the same chromatic polynomial, and how to determine that the polynomial is chromatic.
Для двудольного графа задача раскраски вычисляется за линейное время с помощью поиска в ширину. В случае совершенных графов, хроматическое число и соответствующая ему раскраска может быть найдена за полиномиальное время при использовании полуопределенного программирования [en] . Точные формулы для нахождения хроматического числа известны для многих классов графов (леса, циклы, колеса, хордальные графы) и так же могут быть вычислены за полиномиальное время.
Алгоритм полного перебора для случая k-раскраски рассматривает все {\ k^{n}} комбинаций расстановки цветов в графе с n вершинами и проверяет их на корректность. Чтобы вычислить хроматическое число и хроматический полином, данный алгоритм рассматривает каждое k от 1 до n. Такой алгоритм на практике может быть применим только для небольших графов.
Используя динамическое программирование и оценку размера наибольшего независимого множества, в графе возможность k-раскраски может быть разрешена за время {\ O(2,445^{n})} [17] . Известны более быстрые алгоритмы для 3- и 4-раскрасок, работающие за время {\ O(1,3289^{n})}
[18] и {\ O(1,7272^{n})}
[19] соответственно.
Стягивание вершин — это операция, которая из графа {\ G} делает граф {\ G/uv}
, отождествляя вершины {\ u}
и {\ v}
, удаляя соединяющих их рёбра, и заменяя на одну вершину{\ w}
, куда перенаправляются ребра инцидентные вершинам {\ u}
и {\ v}
. Эта операция играет важную роль в анализе раскраски графов.
Хроматическое число удовлетворяет рекуррентному соотношению:
{\ \chi (G)=min\{\chi (G+uv),\chi (G/uv)\}} ,
где {\ u} и {\ v}
несмежные вершины, {\ G+uv}
граф с добавленным ребром {\ uv}
. Некоторые алгоритмы основаны на данном соотношении, выдавая как результат дерево, иногда называемое деревом Зыкова. Время выполнения зависит от метода выбора вершин {\ u}
и {\ v}
.
Хроматический полином удовлетворяет рекуррентному соотношению:
{\ P(G-uv,t)=P(G/uv,t)+P(G,t)} ,
где {\ u} и {\ v}
смежные вершины, {\ G-uv}
граф с удалением ребра {\ uv}
. {\ P(G-uv,t)}
представляет собой число возможных правильных раскрасок графа, когда вершины {\ u}
и {\ v}
могут иметь одинаковые или различные цвета. Если {\ u}
и {\ v}
имеют разные цвета, тогда мы можем рассмотреть граф, где {\ u}
и {\ v}
смежные. Если {\ u}
и {\ v}
имеют одинаковые цвета, мы можем рассмотреть граф, где {\ u}
и {\ v}
объединены.
Выражения данные выше приводят к рекурсивной процедуре, названной алгоритм удаления и стягивания , сформировавшей основу для многих алгоритмов раскраски графов. Время работы удовлетворяет такому же рекуррентному соотношению, как и числа Фибоначчи, поэтому в наихудшем случае алгоритм будет работать за время {\ ((1+{\sqrt {5}})/2)^{n+m}=O(1,6180^{n+m})} для n вершин и m рёбер. [20] На практике, метод ветвей и границ и отбрасывание изоморфных графов позволяет избежать некоторых рекурсивных вызовов, время работы зависит от метода подбора пары вершин.

Два результата работы жадного алгоритма при выборе разных порядков вершин.
Жадный алгоритм упорядочивает вершины {\ v_{1}} ,…,{\ v_{n}}
и последовательно присваивает вершине {\ v_{i}}
наименьший доступный цвет, не использовавшийся для окраски соседей {\ v_{i}}
среди {\ v_{1}}
,…,{\ v_{i-1}}
, либо добавляет новый. Качество полученной раскраски зависит от выбранного порядка. Всегда существует такой порядок, который приводит жадный алгоритм к оптимальному числу {\ \chi (G)}
красок. С другой стороны, жадный алгоритм может быть сколь угодно плохим; например, корона с n вершинами может быть раскрашена 2 цветами, но существует порядок вершин, который приводит к жадной раскраске из {\ n/2}
цветов.
Для хордального графа и для его особых случаев (например, интервальный граф) алгоритм жадной раскраски может быть использован для нахождения оптимальной раскраски за полиномиальное время, выбирая порядок вершин обратным ксовершенному порядку исключения. Этот алгоритм может применен и к более широкому классу графов (совершенно упорядочиваемые графы [en] ), однако найти такой порядок для таких графов — NP-сложная задача.
If the vertices are ordered according to their degrees, the greedy coloring algorithm uses no more than {\ max_ {i} min \ {d (v_ {i}) + 1, i \}} colors, which is a maximum of 1 more than {\ \ Delta}
(here {\ d (v_ {i})}
- degree of vertex {\ v_ {i}}
). This heuristic algorithm is sometimes called the Welsh-Powell algorithm. [21] Another algorithm sets the order dynamically, choosing the next vertex of the one that has the greatest number of adjacent vertices of different colors. Many other graph coloring algorithms are based on greedy coloring and use static or dynamic strategies for choosing the order of vertices.
In the field of distributed algorithms there is a similar problem. Suppose graph vertices are computers that can communicate with each other if they are connected by an edge. The challenge is for each computer to choose a “color” for itself, so that the neighboring computers choose different colors. This task is closely related to the problem of symmetry breaking. The most developed probabilistic algorithms work faster than deterministic algorithms for graphs with a sufficiently large maximum degree of vertices {\ \ Delta} . The fastest probabilistic algorithms use the technique of multiple attempts [en] [22] .
In symmetric graphs, deterministic distributed algorithms cannot find the optimal coloring of the vertices. Additional information is needed to avoid symmetry. A standard assumption is made that initially each vertex has a unique identifier, for example, from the set {\ \ {1,2, ..., N \}} . In other words, it is assumed that we are given an n- coloring. The goal is to reduce the number of colors from n to, for example, {\ (\ Delta +1)}
. The more colors are used (for example, {\ O (\ Delta)}
instead of {\ (\ delta +1)}
), the less message exchanges will be required [22] .
A simple version of the distributed greedy algorithm for {\ (\ Delta +1)} coloring requires {\ \ Theta (n)}
communication rounds are at worst - information may have to go from one end of the network to the other.
The simplest interesting case is the n- cycle. Richard Cole and Uzi Vishkin [23] showed that there is a distributed algorithm that reduces the number of colors from n to {\ O (log (n))} by using only one message exchange between neighbors. Repeating the same procedure, we can get the 3-coloring of the n- cycle for {\ O (log ^ {*} (n))}
communication rounds (provided that unique node identifiers are given).
{{ log ^ {*}} function , the iterated logarithm, is an extremely slow growing function, "almost constant." Consequently, the results of Cole and Vishkin raise the question of whether there is a distributed n-cycle 3-coloring algorithm that runs in constant time. Nathan Lineal showed that this is impossible: any deterministic distributed algorithm requires {\ \ Omega (log ^ {*} (n))}
communication rounds to reduce N -coloring to 3-coloring in the n-cycle. [24]
The Cole and Vishkin techniques can also be applied to an arbitrary graph with a limited degree of vertices, in this case the running time is {\ P (\ Delta) + O (log ^ {*} (n))} . [25] This method was generalized for the graph of unit circles by Schneider et al. [26]
The problem of coloring the edges was also studied in a distributed model. Pansonezzi and Rizzi reached {\ (2 \ Delta -1)} coloring for {\ O (\ Delta + log ^ {*} (n))}
in this model. [27] The lower limit for the distributed coloring of the vertices achieved by Linial is also applicable to the problem of distributed edge coloring. [24]
Decentralized algorithms are those in which internal messaging is not allowed (as opposed to distributed algorithms, where processes exchange data with each other). There are effective decentralized algorithms that successfully cope with the task of coloring graphs. These algorithms work on the assumption that the vertex is able to “feel” that any of its neighboring vertices is painted in the same color as it. In other words, it is possible to determine a local conflict. Such a condition is quite often performed in real applications - for example, when transmitting data over a wireless channel, a transmitting station, as a rule, has the ability to detect what the other station is trying to transmit simultaneously to the same channel. The ability to obtain such information is sufficient to ensure that algorithms based on learning automata [en] with a probability of one correctly solve the problem of coloring the graph [28] [29] .
Coloring a graph is computationally challenging. To find out whether the graph k allows 7-coloring for a given k is an NP-complete problem, except for the cases k = 1 and k = 2. In particular, the problem of calculating the chromatic number is NP-complex. [30] The 3-coloring problem is NP-complete even for the case of a planar graph of degree 4. [31]
Also, an NP-challenge is the coloring of a 3-colored graph with 4 colors [32] and a k- colored graph {\ k ^ {log (k) / 25}} for sufficiently large values of k . [33]
Calculating the chromatic polynomial coefficients # P complex task. It is proved that there is not a single FPRAS algorithm for calculating the chromatic polynomial for any rational number k ≥ 1.5, except k = 2, unless it is satisfied that NP = RP. [34]
Coloring vertices models many planning problems. [35] In its simplest setting, a given set of works should be distributed over time intervals, each such work takes one segment. They can be performed in any order, but two jobs may conflict in the sense that they cannot be performed simultaneously, since, for example, they share resources. The corresponding graph contains a vertex for each of the jobs and an edge for each conflicting pair. The chromatic number of the constructed graph is the minimum execution time for all jobs without conflicts.
Details of the planning problem determine the structure of the graph. For example, when airplanes are distributed among flights, the resulting conflict graph is an interval graph, so the coloring problem can be solved effectively. The distribution of radio frequencies results in a graph of unit circles of conflicts, and for such a problem there is a 3-approximation algorithm.
A compiler is a computer program that translates one computer language into another. To improve the execution time of the resulting code one of the techniques of compiler optimization, is the distribution of registers in which the most frequently used variables of the compiled program are stored in high-speed registers of the processor. In the ideal case, variables are stored in registers so that they are all in registers during their use.
The standard approach to this problem is to reduce it to the problem of coloring graphs. [8] The compiler builds an interference graph , where vertices correspond to registers, and the face connects two of them, if they are needed at the same time. If this graph is k- chromatic, then the variables can be stored in k- registers.
Digital watermarking technology (English digital watermarking ) allows along with data (whether it be media files, executable files, and others) to transmit some hidden message ("watermark", Watermark ). Such a hidden message can be used in copyright protection to identify the owner of the data.
This is important, for example, to determine the source of their distribution in an illegal manner. Or to confirm the rights to the data, for example - software systems on a chip ( system-on-chip ).
The message can be encoded including in the method of register allocation. One of these techniques was suggested by Qu and Potkonjak [36] (therefore, it is sometimes called the QP algorithm).
It is this: let {\ G} - incompatibility graph (interference graph) of the distribution of processor registers, which was mentioned above. Its coloring is used in the program - and, it is used in such a way that it is permissible to change the contents of the graph with a small increase in its chromatic number. It turns out that it is possible to encode a message in a software product using the coloring of the graph {\ G}
, i.e. register allocation.
You can extract this message by comparing the distribution of registers with the original coloring; [37] There are also ways to ascertain whether a certain message was encoded in the program without using the original one.
Later, different authors developed and refined the ideas of Qu and Potkonjak . [38] [39] [37]
The task of coloring graphs has been posed in many other areas of application, including pattern matching.
Solving the Sudoku puzzle can be seen as the completion of the coloring with 9 colors of a given graph of 81 vertices.
Coloring graphs (continued) Algorithm coloring graph.
A variety of tasks arising from production planning, scheduling inspection, storage and transportation of goods, etc., can often be presented as problems of graph theory, closely related to the so-called “coloring task” . The graphs considered in this part are unoriented and do not have loops.
 Let G = (V, E) be an arbitrary graph and {c i , ..., c t } be some set whose elements will be called colors. The t-coloring of a graph G is a map φ of V {{c i , ..., c t } such that for any two distinct adjacent vertices and and v of the graph G, Φ (u)! = Φ (v).
Let G = (V, E) be an arbitrary graph and {c i , ..., c t } be some set whose elements will be called colors. The t-coloring of a graph G is a map φ of V {{c i , ..., c t } such that for any two distinct adjacent vertices and and v of the graph G, Φ (u)! = Φ (v).
We note that it is not assumed here that φ maps V to the entire set of colors {c i , ..., c t }. We say that the color of Φ (v) is assigned to the vertex v of GV or the vertex of v has the color of Φ (v). We see that the t-coloring of the graph G attributes to each of its vertices one of the t given colors in such a way that any two different adjacent vertices have a different color.
Tricolor coloring Count Petersen
A graph is called t-colored if it possesses t-coloring. A graph is called t-chromatic if it is t-colorable, but not (t - 1) -colorable; the number t in this case is called the chromatic number of the graph G and denoted by x (G).
notice, that
1) 1-chromatics graphs are zero graphs and only they;
2) 2-chromatic graphs are non-zero bipartite graphs and only they;
3) x (K n ) = n and x (G)> = n if the graph G contains the graph K n for a natural number n as a subgraph.
The problem of finding the chromatic number of an arbitrary graph has been the subject of many studies at the end of the 19th and in the current century. Now on this issue a large number of interesting results are known. In this section, we consider an “approximate” algorithm that allows us to find the value of the chromatic number of an arbitrary graph and the coloring of the vertices corresponding to this value.
"Approximate" graph coloring algorithm
The graph coloring algorithm allows finding the (exact or approximate) value of the chromatic number of an arbitrary graph and the corresponding color of the vertices.
A graph G is called r-chromatic if its vertices can be colored using r colors (colors) so that there are no two adjacent vertices of the same color. The smallest number r such that the graph G is r-chromatic is called the chromatic number of the graph G. The task of finding the chromatic number of a graph is called the coloring problem (or coloring problem) of the graph. Corresponding to this number, the coloring of the vertices splits the set of vertices of the graph into r subsets, each of which contains vertices of the same color. These sets are independent, because within the same set there are no two adjacent vertices.
Consider a sequential method based on the ordering of a set of vertices.
Colourize (G)
1. Arrange the vertices by non-increasing degree.
2. Color the first vertex in color 1.
3. Select a color 1.
4. Until all the vertices are colored, repeat clauses 4.1.-4.2 .:
4.1. Color in the selected color any vertex that is not adjacent
on the other, already painted in this color.
4.2. Select the next color.
In this simplest of methods, the vertices are initially arranged in the order of non-increasing degrees. The first vertex is colored 1; then the list of vertices is viewed from top to bottom (by non-increasing degrees) and in color 1 every vertex is colored, which is not adjacent to another, already painted in this color. Then we return to the first unpainted vertex in the list, paint it in color 2 and again look at the list of vertices from top to bottom, paint in color 2 any unpainted vertex that is not connected by an edge with another vertex painted in color 2. Similarly, we act with colors 3, 4, etc., until all vertices are colored. The number of colors used will then be an approximate value of the chromatic number of the graph.
The above algorithm can be modified. To do this, after each step, you need to order the unpainted vertices. A simple modification of the heuristic procedure described above consists in reordering the unstained vertices by non-increasing their relative degrees. Relative degrees are understood to be the degrees of the corresponding vertices in the uncolored subgraph of the original graph.
In this modification it was assumed that if two vertices have the same degree, then the order of such vertices is random. Such vertices can also be ordered, but by two-step powers. We define a two-step degree as the sum of the relative degrees of the incident vertices. Similarly, you can proceed further.
Disregarding the time spent on sorting the vertices in the order of non-increasing degrees, it is necessary to loop through all the vertices of the graph. For each one, it is necessary to find the minimum color, which in the worst case may take o (V 2 ) for the case with a full graph. This means that the total time will be o (V 3 ) in the worst case.
Algorithm Visualizer:
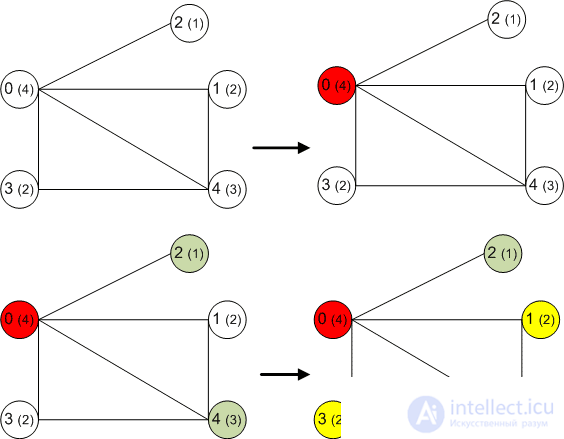
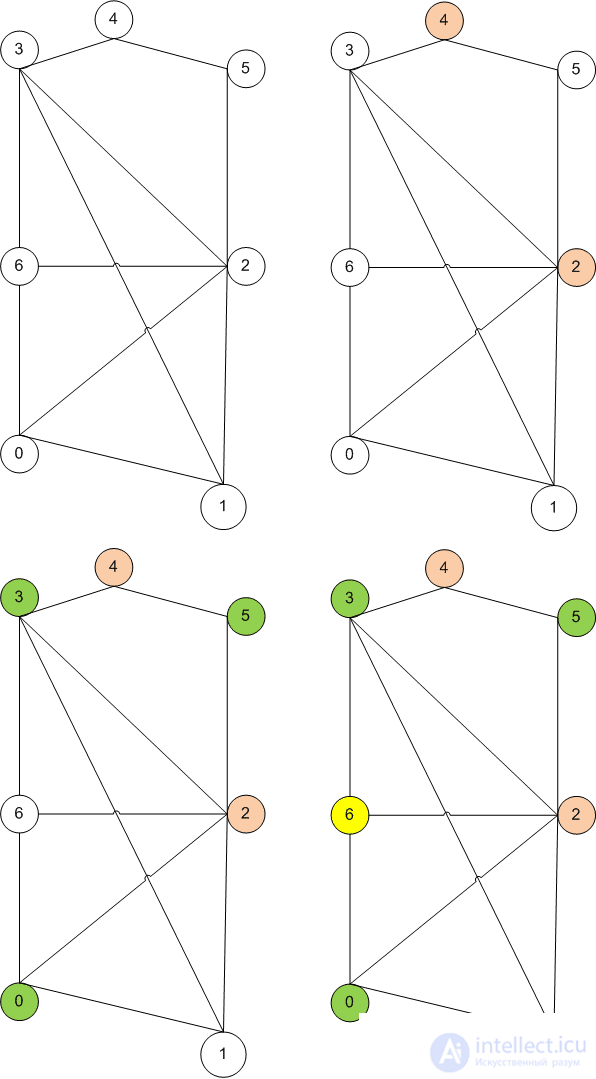
For a start, you can limit the chromatic number of the graph G from below to the click number of the graph. This is obvious because the coloring of a graph click will require a number of colors equal to the number of vertices of this click.
γ ( G ) ≥ ρ ( G )
Now we introduce a more accurate estimate. We use for this the number of vertices in the maximal independent set of the graph G. α ( G ) = ρ ( G ′), where the graph G ′ is the complement of the graph G.
γ ( G ) ≥ [ n / α ( G )] or γ ( G ) ≥ [ n / ρ ( G ′)],
where [] is the integer part of a number. Consider two more estimates introduced in [2].
γ ( G ) ≥] 2 n 0.5 [−γ ( G ′)
γ ( G ) ≥ n / γ ( G ′),
where] [means the smallest integer that is not less than the argument. There is one more estimate, less accurate than the first, but using only the number of vertices and edges of the graph.
γ ( G ) ≥ n 2 / ( n 2 −2 m )
As a result, we can say that the estimates given are rather inaccurate. For example, in [3] it was shown that it is possible to construct a graph that does not even contain a complete third-order subgraph and will have an arbitrarily large value of the chromatic number. At the same time, these estimates give approximately the same accuracy. Therefore, the choice of them should be made on the basis of already calculated data.
The lower estimates of the chromatic number are certainly more interesting than the upper ones, since (if they are close enough to the true value) they can be used in the procedure for calculating γ ( G ), including the search tree. At the same time, the upper estimates of the chromatic number of such applications are not found. Nevertheless, formulas are given in the literature for calculating the upper estimates of the chromatic number. For example, in [1], the following easy-to-calculate estimate was proposed:
γ ( G ) ≤ 1 + max ( d ( x i +1)), x i ∈ X
We also give two estimates linking the chromatic number of the graph and the chromatic number of the complement for this graph.
γ ( G ) ≤ n + 1 − γ ( G ′)
γ ( G ) ≤ [( n +1) 2/4] / γ ( G ′)
The above upper and lower bounds using the chromatic number of the complement of the graph under consideration are the most accurate in the sense that it is possible to construct graphs on which these bounds are achieved. But in most cases they are so inaccurate that they have no practical value.
For a long time, the following theorem was the best estimate for planar graphs.
Each planar graph can be so colored using five colors so that any two adjacent vertices will be colored in different colors.
And in 1850, the first mentions of the four color hypothesis appeared, which was an improved estimate for planar graphs. This hypothesis was substantiated by computer in 1976, and later proved analytically and received the status of a theorem.
Each planar graph can be colored in such a way, using four colors, that any two adjacent vertices will be colored in different colors.
If the graph G is r- chromatic, then it can be colored using r (or fewer) colors using the following procedure: first, some maximum independent set S ( G ) is colored in one color, then set S is colored into the next color ( X \ S ( G )) and so on until all vertices are colored.
Evidence. The fact that such a coloring, using only r colors, always exists, can be set as follows. Suppose there exists a coloring in r colors, such that one or more sets painted in the same color are not maximal independent sets in the sense mentioned above.
The advantage of this method is that it takes into account cache sizes, cache lines, code “blocks”, and cache associativity. The method is successfully combined with other optimizations and inline-functions [10] [11] . It should be noted that it can be implemented by the optimizer - but not by the optimizer of the compiler, but by the optimizer of the linker.
(Eng. Spectrum management , Eng. frequency allocation )
A good work classifying such problems and systematically setting out their solutions is [12] .
The term “frequency allocation” unites different types of tasks, which often have different goals and models. These tasks include:
The common thing between tasks is that they all produce an optimal distribution of a limited set of radio spectrum resources among users, the number of which is constantly growing in modern conditions.
Two main areas of optimization here:
In the course of considering suitable models, in [12] , problems arise not much more complicated than T-coloring (English T-coloring ) of a multigraph, list T-coloring (English set T-coloring ).
As an example of work on a real cellular network, the results of which were further applied by the operator in their practical activities - [13] (Conducted by the operator E-Plus ((eng.) En: E-Plus) - the 3rd largest in Germany (2010 )).
To summarize, we will present the problem as follows: objects are certain calculations between which it is necessary to divide the computing resources (processors, computers ...) that can work in parallel with each other. Some calculations can be performed in parallel to each other, some - no. Accordingly, the vertex coloring of the incompatibility graph of the calculations is the desired distribution.
Let us give the following examples of numerical methods that can be parallelized in this way:
Cholesky decomposition for the conjugate gradient method with predestination
See also: en: Conjugate gradient method # The preconditioned conjugate gradient method
[14] This method is one of the best iterative methods for solving systems of linear algebraic equations (SLAE) with large, sparse, symmetric, positively defined matrices.
Gauss – Seidel method as applied to sparse matrices
The same iterative method for solving SLAU.
This, in turn, is good, for example, for calculating power distribution grids: such networks can be represented by graphs whose vertices are consumers and sources of electricity, and the edges are power lines; further, a SLAE is constructed, in the matrix of which the diagonal elements correspond to the nodes of the aforementioned graph, and non-zero non-diagonal elements correspond to edges. [15]
Also, the method can be so-called. smoother (English iterative smoother ) for multigrid finite element problem solving methods. (English multigrid methods of finite element problems ). Optimization of the Gauss – Seidel method used in smoothing using the so-called English sparse tiling for such a case of its use is considered in [16] .
Methods using adaptive refined mesh
(English Adaptive mesh refinement )
[17] They, in turn, are useful in solving partial differential equations (DPEs). The clarification principle here is this: in places where the greatest local error is expected — where the solution changes most rapidly, the grid density is chosen to be greater.
Coordinate relaxation method
(eng. method of coordinate relaxation )
[18] It is successfully used in finding the extremal eigenvalues of very large sparse symmetric matrices. Sometimes so large that it is more practical to generate them on the fly than to store them in memory. Such problems often arise in quantum mechanics.
Predetermining incomplete LU decomposition
( Preconditioning by ILU, Incomplete LU-factorization )
To solve the slau using the Krylov subspaces. [nineteen]
Calculation of matrices of derivatives (Jacobians and Hessians) in the case when they are sparse, can be seriously accelerated by coloring the graphs. There is a project "Graph Coloring for Computer Derivatives", site - [www 3] . The site contains publications on the topic, as well as - a software package, in which the project participants have drawn up their achievements. For an introduction to the subject, you can see one of the presentations related to the project - [20] .
For a simple case when the “compaction” of a derivative is limited to a decrease in the number of columns, we give an algorithm:
| Input : function from vector - Output : derivative 1. Investigate the structure of the sparseness of the derivative 2. Make a matrix 3. Calculate the compacted values 4. And now, restore the values |
Coloring graph here - in the calculation . In simple cases, it is necessary to calculate the usual vertex (born distance-1 ); distance-2 coloring (which, including reduced to square -distance distance-1 coloring); in more complex, small additional restrictions are required:
Within the framework of the above project, calculations were carried out for technical production problems:
Digital watermarking technology (English digital watermarking ) allows along with data (whether it be media files, executable files, and others) to transmit some hidden message ("watermark", Watermark ). Such a hidden message can be used in copyright protection to identify the owner of the data.
This is important, for example, to determine the source of their distribution in an illegal manner. Or to confirm the rights to the data, for example - software systems on a chip ( system-on-chip ).
The message can be encoded including in the column. One of these techniques was proposed by Qu and Potkonjak (therefore, it is sometimes called the QP algorithm) in [21] .
It consists of this: let's say we have a graph G, the coloring of which is used in the program - moreover, it is used in such a way that it is permissible to change the contents of the graph with a slight increase in its chromatic number. What is important, one of such examples is the incompatibility graph of the register of the processor, which was mentioned above, which means that we will be able to encode the message in a software product using the distribution of registers.
You can extract it by comparing the resulting graph with the original one; there are also ways to ascertain whether a message was encoded in the graph without using the original one — the extraction is described in more detail, for example, in [22] .
The development and refinement of the thoughts of Qu and Potkonjak , attempts to improve the algorithm occur in [23] , [24] , [22] .
Note that in [23] , [24] there are references to the SandMark software package, in which algorithms of this kind are executed; available for download at [www 4] .
Comments
To leave a comment
Algorithms
Terms: Algorithms