Lecture
4 vertex tournament
tops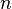 
ribs: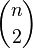 
A tournament is a directed graph obtained from an undirected full graph by assigning a direction to each edge. Thus, a tournament is a digraph in which each pair of vertices is connected by one directed arc.
Many important tournament features have been reviewed by Landau [1] in order to investigate the chick dominance model in the flock. Current tournaments applications include research in the field of voting and collective choice among other things. The name of the tournament comes from the graphical interpretation of the outcomes of a round-robin tournament, in which each player meets each other player exactly once, and in which there can be no draws. In the tournament digraph, the tops correspond to the players. The arc between each pair of players is oriented from the winner to the loser. If a player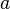 
wins the player 
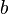then say that 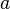dominates .
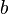Any tournament with a finite number 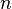vertices contains a Hamiltonian path, that is, an oriented path containing all 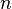vertices [2] . This is easily shown by mathematical induction on 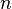: let the statement be true for 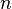and let there be some tournament 
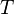with 
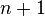tops. Pick vertex 
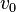at 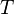let it go 
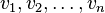- directional path to 
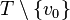. Let be 
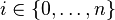- the maximum number, such that for any 
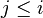there is an arc of 
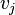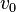at . Way
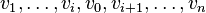
- the desired oriented path. This proof also provides the search algorithm for the Hamiltonian path. Known more efficient algorithm that requires iteration of all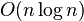 
arcs [3] .
This means that a strictly connected tournament has a Hamiltonian cycle [4] . More strictly: any strongly connected tournament is vertex-pancyclic [en] - for any vertex v and for any k from three to the number of vertices in the tournament there is a cycle of length k containing v . [5] . Moreover, if a tournament is 4-connected, any pair of vertices can be connected by the Hamiltonian path [6] .
Transitive tournament with 8 vertices.
Tournament in which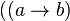 
and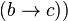 
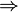
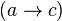is called transitive . In a transitive tournament, tops can be completely ordered in order of reachability.
The following statements for a tournament with n vertices are equivalent:
Transitive tournaments play a significant role in Ramsey theory, similar to the role played by clicks in undirected graphs. In particular, any tournament with n vertices contains a transitive sub-tournament with 
tops. [7] The proof is simple: choose any vertex v as a part of this subtournament and construct a subtournament recursively on the set of either the incoming neighbors of the vertex v or the set of outgoing neighbors, depending on which set is larger. For example, any tournament with seven peaks contains a transitive tournament with three peaks. The seven-top Paley Tournament shows that this is the maximum that can be guaranteed [7] . However, Reid and Parker [8] showed that this boundary is not strict for some large values of the number n .
Erdos and Moser [7] proved that there are tournaments with n vertices without transitive size sub-tournaments.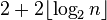 
. Their proof uses counting [en] : the number of variants in which a transitive tournament with k vertices can be contained in a larger tournament with n marked vertices is equal to
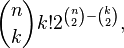
and with k superior 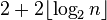this number is too small for a transitive tournament to be in each of 
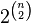different tournaments of the same set of n marked vertices.
The player who wins all the games will naturally be the winner of the tournament. However, as the existence of nontransitive tournaments shows, such a player may not be. A tournament in which each player loses at least one game is called a 1-paradoxical tournament. Generally, a Tournament T = ( V , E ) is called k- paradoxical, if for any k -element subset S of V there is a vertex v 0 in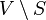 
such that 
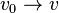for all 
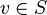. Using the probabilistic method [ru], Erdёs showed that for any fixed k subject to | V | ≥ k 2 2 k ln (2 + o (1)) almost any tournament on V is k- paradoxical. [9] On the other hand, a simple argument shows that any k- paradoxical tournament must have at least 2 k +1 - 1 players, which has been improved to ( k + 2) 2 k −1 - 1 Esther and Györgye Sekresres ( 1965) [10] . There is an explicit method for constructing k- paradoxical tournaments with k 2 4 k −1 (1 + o (1)) players, developed by Graham and Spencer, namely, Paley's tournament [11] .
Condensation [en] of any tournament is a transitive tournament. Thus, even if a tournament is not transitive, the strongly related components of a tournament can be completely streamlined. [12]
The sequence of a tournament score is a non-decreasing sequence of half-degrees of the outcome of the tournament tops. The tournament score set is the set of integers that are semi-degrees of the outcome of the tournament tops.
Landau's theorem (1953) Non-decreasing sequence of integers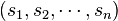 
is a counting sequence if and only if:
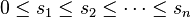
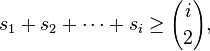for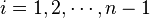 
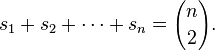
Let be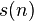 
- number of different size counting sequences 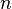. Sequence 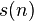begin with:
1, 1, 1, 2, 4, 9, 22, 59, 167, 490, 1486, 4639, 14805, 48107, ...
(sequence A000571 in OEIS)
Winston and Kleitman proved that for sufficiently large n
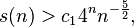
Where 
Takacs later showed [13] using some plausible but unproved assumption that
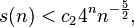
Where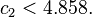 
Together, this suggests that
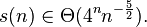
Here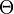 
reflects the asymptotically strict boundary.
Yao showed [14] that any non-empty set of non-negative integers is a score set for some tournament.
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.