Lecture
Consider the set A = {a1, a2, ..., аn} containing n different elements, which will be called the n-set
or a general population of volume n. From the n-set it is possible to form its parts (subsets).
Definition A subset consisting of m elements of an n-set is called an m-subset of an n-set or
a union of n elements by m, or a sample of volume m from the total population of volume n.
There are two possible choices:
1. Selection without return, in which the once selected item is removed from the population. Sample
(connection) in this case does not contain duplicate elements.
2. The choice with the return, in which the choice is made every time from the whole population, that is, before
the next choice is the previous selected item is returned to the population. In the sample (compound) in
In this case, there are repetitions.
Which samples of the same volume are considered different and which are the same, depends on the rules for selecting compounds
(subsets, selections).
Two compounds may differ either by 1) composition, if they contain at least one different element, or
2) the order of incoming items.
Depending on the rules for selecting a compound, they are divided into three types: placement, permutation, combination. Depending on the
The method of choice (without return or return), each type of connection can be without repetitions or with repetitions.
2. Placement with and without repetitions.
The classical task of combinatorics is the problem of the number of placements without repetitions, the content of which can be
to express the question: in how many ways can m be selected and placed in m different places from n different objects?
Also the classical task of combinatorics is the problem of the number of placements with repetitions, the content of which
can be expressed by the question: in how many ways can m be selected and placed in m different places from n objects,
among which are the same?
Definition The arrangements of n elements by m are called compounds of n elements by m, which differ
from each other, either by their elements (composition) or by their order.
In the language of set theory, it sounds like this: placements of n elements by m are ordered
The m-subset of the n-set (ordered m-sample from the general population of volume n). The term "orderly"
means that the order of the elements in the sample is significant: samples with the same elements, but with different
the order of their following are different.
Task . Let there be a set containing 4 letters:
{A, B, C, D}. Record all possible placements of 4 specified letters of two:
a) without repetition;
b) with repetitions.
Decision.
a) Such placements 12: (AB), (AC), (AD), (BC), (BD), (BA), (CA), (CB), (CD), (DA), (DB), (DC). notice, that
placements differ in the order of their elements and their composition. The locations of AB and BA contain the same letters,
but their order is different.
b) Such placements 16. For those given for case (a)
placements are added to placements of the same elements (AA), (BB), (CC), (DD).
Task . Let there be a set containing 2 letters: {A, B}. Record all possible placements with repetitions from
4 letters.
Decision. Such placements 16: (AAAA), (BBBB), (AAAB), (AABA), (ABAA), (BAAA), (AABB), (ABAB), (BABA), (BBAA), (ABBA),
(BAAB), (BBBA), (BBAB), (BABB), (ABBB).
Theorem 3. 3.1 The number of different arrangements without repetitions.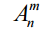 
of n elements by m equals
for sampling without return.
3.2 Number of layouts with repetitions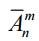 
of n elements with m equal 
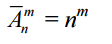(2) for the sample with the return.
Evidence. For the proof, we use the multiplication rule.
Consider samples without return. There are n possibilities to select the first element, the second - (n - 1)
(before the second choice in the general population there are (n –1) elements), ..., with the m-th choice of (n - m + 1) possibilities.
Thus, according to the multiplication rule
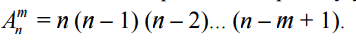
. We write the expression in a more convenient form by multiplying and dividing it by (m - n)!
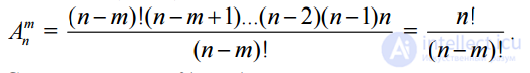
. It is considered that 0! = 1, which allows using this formula for the case m = n.
Consider returning samples . There are n possibilities for choosing the first element, and n for the second element (before
rum of the next element the previous selected element is fixed and returned to the general population), with m-th you
Bor too n opportunities. In this way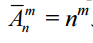 
.
Task . In some newspaper 12 pages. It is necessary to place four photographs on the pages of this newspaper.
How many ways can this be done if no single page of a newspaper should contain more than one photo?
The decision . In this problem, the general population is 12 pages of a newspaper, and 4 selected pages for photographs are a sample without return. In this task, it is important not only which pages are selected, but also in what order (for arranging photos). Thus, the task is reduced to the classical problem of determining the number of placements without repetitions of 12 elements with 4 elements:
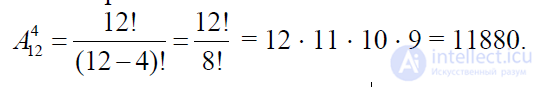
Thus, 4 photos on 12 pages can be arranged in 11880 ways.
Task . The boy left from the set for the board game stamps with the numbers 1, 3 and 7. He decided with the help of these
stamps put on all books five-digit numbers - make a catalog. How many different five-digit numbers can
to put a boy?
Decision. We can assume that the experience consists in a 5-fold choice with the return of one of 3 figures {1, 3, 7}. Thus, the number of five-digit numbers is determined by the number of allocations with repetitions of 3 elements of 5 each:
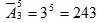
3. Permutations without repetitions
The classical task of combinatorics is the problem of the number of permutations without repetition, the content of which can be
to express the question: how many ways can you place n different objects in n different places?
Definition Locations in which all n elements of the entire population participate are called permutations.
Kami without repetitions of n elements. Permutations consist of the same elements, but differ in order.
Task . Let there be a set of letters {A, B, C}. Record all possible permutations.
Decision. This set of letters corresponds to 6 permutations: (ABC), (ACB), (BAC), (BCA), (CBA), (CAB).
Theorem . The number of permutations of n different elements is n !, that is, Pn = n!
Evidence. Since permutations are a particular case of arrangements, for n = m we get
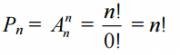
Comment. For large n, the factorial logarithm or Stirling approximate formula is used to calculate factorial
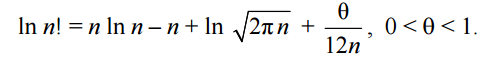
Task . How many four-letter “words” can be made from the letters “marriage”?
The decision . The general totality are 4 letters of the word "marriage" {b, p, a, k}.
The number of "words" is determined by permutations of these 4 letters, i.e. P 4 = 4! = 1 x 2 x 3 x 4 = 24.
Task . In how many ways can you place nine different books on a shelf so that certain four books stand side by side?
The decision . In the original population - 9 different books.
We will consider the selected 4 books for one.
Then for the remaining 6 books there is a P 6 = 6! = 720 permutations.
However, four specific books can be rearranged among themselves P 4 = 4! = 24 ways.
By the multiplication rule, we have P 6 x P 4 = 720 x 24 = 17280.
4. Permutations with repetitions
For the case when among the selected n elements there are the same (sampling with return), the problem of the number of permutations with repetitions can be expressed by the question: how many ways can you rearrange n items located on
n different places, if among n items there are k different types (k
Definition Permutations with repetitions are called compounds from the general population, each of which contains n elements, among which is the element
A1 is repeated n1 times
A2 is repeated n2 times
. . . . . . . . . . . . . . . . . . .
an is repeated nk times
n1 + n2 + ... + nk = n
and which differ from each other only in the arrangement of the various elements.
Theorem. The number of permutations with repetitions
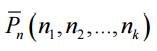equally
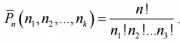
. Evidence. The proof is obvious, since permutations of identical elements in a permutation with repetitions do not give a new permutation.
Task .
How many different letter combinations can be made from the letters of the word "Mississippi"?
Decision. Here there is 1 letter “m”, 4 letters “i”, 3 letters “c” and 1 letter “p”, a total of 9 letters.
Therefore, the number of permutations with repetitions is
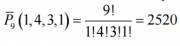
5. Combinations without repetitions
The classical task of combinatorics is the problem of the number of combinations without repetitions, the content of which can be expressed by the question: in how many ways can m be chosen from n different objects?
Definition Combinations of n different elements of m are called compounds of n elements of m (m <= n), which
differ from each other only in the composition of the elements.
Task. Let there be a set containing 4 letters {A, B, C, D}. We write down all the possible combinations of these
letters on 3.
Decision. There are 4 such combinations: ABC, ACD, ABD, BCD.
Here, the number of combinations does not include, for example, DIA, ICA, as they do not differ in composition from sequential
ABC letters, because rearranging elements of a new combination does not.
Theorem. The number of combinations of n elements is equal to m
.
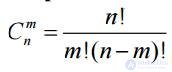Evidence.
Recall that both combinations and arrangements of n elements by m are samples of volume m from the general population of volume n and the difference between them is that in the case of allocations both the composition and the order of elements are important, whereas in the case of combinations only the composition is important items. Let there be any one combination. In order to form all placements with the same elements, it is necessary to carry out all sorts of permutations of the elements of this combination. Since m is combined, there is m! permutations. Therefore, one combination consisting of m elements corresponds to m! placements with these elements. therefore
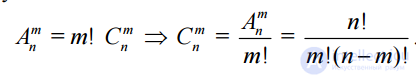
Numbers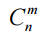 
called binomial coefficients: they are coefficients in the Newton binomial decomposition
Task . It is necessary to choose as a gift 4 out of 10 different books available. How many ways can this be done?
The decision . The general population is 10 different books. Of these, you need to choose 4, and the order of selection of books does not matter. It is necessary to find the number of combinations of 10 elements by
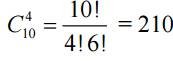
Task . There are 10 white and 5 black balls. In how many ways you can choose 7 balls, so that among them were 3 black?
The decision . We have 15 balls: 10 white and 5 black. You need to choose 7 balls: 4 white and 3 black.
We divide 15 balls into 2 general populations:
1) 10 white balls;
2) 5 black balls.
4 white balls will be chosen from the I population, the order of choice is indifferent, you can choose
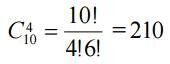in ways. 3 black balls will choose from the II general population, you can choose
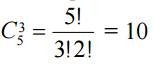in ways.
Then, according to the multiplication rule, the desired number of ways is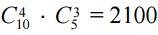 
.
The solution to this problem can be schematically presented as follows
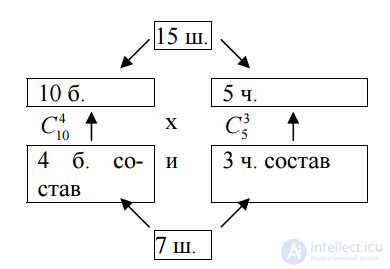
Task . Ten teams participate in the championship of football, the best of which occupy the 1st, 2nd and 3rd place.
Two teams that took the last places will not participate in the next such championship.
How many different variants of the result of the championship can be, if we consider only the position of the first three and the last two teams.
The decision . There is a general population of 10 teams. From it we will choose 5 teams in 2 stages:
1) first to the first 3 places out of 10, taking into account the composition and order of teams
2) then to the last 2 places from the remaining 7, taking into account only the composition (the order of the retired teams is not important).
The first 3 places can be distributed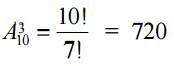 
in ways.
The number of ways to exclude 2 teams from the remaining 7 equals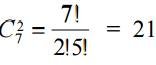 
.
According to the multiplication rule, we find that the number of different inequality results is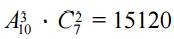 
0
The solution to this problem can be schematically presented as follows:
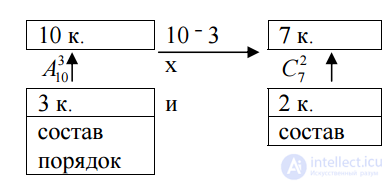
Task .
How many polling options are available for 11 students in one lesson, if none of them will be surveyed twice and any number of students in the lesson can be interviewed, and the order in which the students are interviewed is indifferent?
The decision .
I way. There is a general population of 11 students. The teacher may not interview any of the 11 students, which is one of the options. This case corresponds to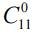 
. The teacher can only interview one of the students, such options 
.
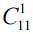If the teacher interviews two students, the number of survey options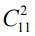 
. For the survey of three students there is 
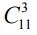options, etc.
Finally, all students can be interviewed. The number of options in this case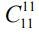 
.
The number of all possible polling options can be found by the addition rule.
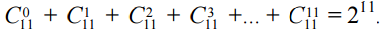
The solution to this problem can be schematically presented as follows:
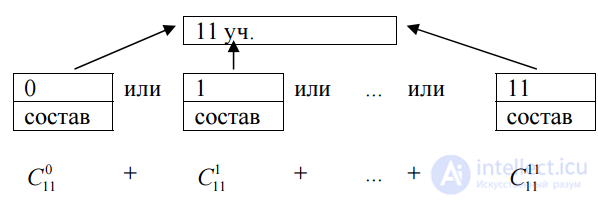
II way. Имеется генеральная совокупность, состоящая из 2 элементов:
{а, в}, где а – ученик опрошен, в – ученик не опрошен на данном занятии.
Опыт состоит в 11-кратном выборе с возвращением одного из элементов этого множества – каждый из 11 учеников либо опрошен, либо не опрошен.
В данной задаче важно не только то, какие выбраны элементы множества (сколько учеников опрошено и сколько нет),
но и в каком порядке (т. е. какой именно ученик опрошен или нет).
Число способов такого выбора определяется числом размещений с повторениями из 2 элементов по 11;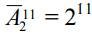 
.
6. Сочетания с повторениями
Рассмотрим задачу о числе сочетаний с повторениями:
имеется по r одинаковых предметов каждого из n различных типов;
сколькими способами можно выбрать m (m <= r) из этих (nxr) предметов?
Definition Сочетаниями с повторениями называются соединения из n элементов по m (выбор с возвращением m элементов), которые отличаются только составом и при этом отдельные соединения могут содержать повторяющиеся элементы.
Задача . Имеются 2 буквы А, 2 буквы В, 2 буквы С. Сколькими способами можно выбрать две из этих шести букв?
Decision. Существует 6 способов выбора 2 букв из 6 с повторениями: (АА), (AB), (AC), (BC), (BB), (CC). Порядок следо-
вания букв не учитывается.
Theorem . Число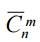 
сочетаний с повторениями равно
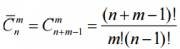
. Evidence. Пусть имеются предметы n различных типов. Сколько соединений по m элементов можно из них сделать, если не принимать во внимание порядок элементов. Расположим в каждом сочетании элементы по типам (сначала все элементы 1-го типа, потом 2-го и т. д.). После этого перенумеруем все элементы в сочетании, но к номерам элементов второ- го типа прибавим 1, третьего типа – 2 и т. д. Тогда из каждого сочетания с повторениями получится сочетание без повторений, состоящее из чисел 1, 2,..., n + m – 1, причем в каждое сочетание входит m элементов.
Отсюда следует, что
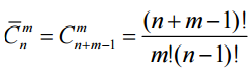
Задача . В технической библиотеке имеются книги по ма- тематике, физике, химии и т. д., всего по 16 разделам науки.
Поступили очередные 4 заказа на литературу. Сколько сущест- вует вариантов такого заказа?
Decision. Так как 4 заказанные книги могут быть и из одно- го раздела науки, и из разных разделов, при этом порядок выбора разделов не важен, то число вариантов заказа определяется чис- лом сочетаний с повторениями из 16 элементов по 4, т. е.
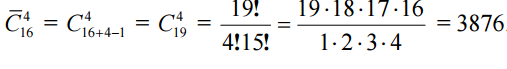
Задача . В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
The decision . Очевидно, что порядок, в котором выбираются пирожные, не существен, причем в комбинации могут входить повторяющиеся элементы (например, можно купить 7 эклеров). Следовательно, число способов покупки 7 пирожных определяется числом сочетаний с повторениями из 4 элементов по 7, т. е
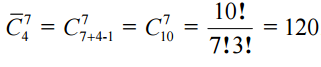
Рассмотрим в этом классе задач две следующие задачи:
1. Даны n различных предметов и k различных групп. Сколькими способами можно распределить n различных предметов по k различным группам, если допускаются пустые группы. Ниже покажем, что число способов равно k^n .
2. Даны n различных предметов и k различных групп. Сколькими способами можно распределить n различных пред- метов по k группам, если в первой группе n 1 предметов, во второй – n 2 , в k-й – n k , где n 1 + n 2 +... + n k = n . Ниже покажем, что число способов равно
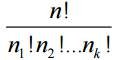
Рассмотрим решение первой задачи. Пусть генеральной совокупностью будет k различных групп {1, 2,..., k}. Можно считать, что опыт состоит в n-кратном выборе с возвращением номера группы для каждого предмета. Заметим, что поскольку предметы разные, то важно не только, какие группы выбираются для предметов, но и в каком порядке выбираются эти группы. Таким образом, число способов раз- бить n различных предметов на k групп определяется числом размещений с повторениями и k элементов по n:
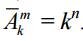
Рассмотрим решение второй задачи.
Разбиение n предметов по k группам можно выполнить следующим образом. Сначала положим все n предметов в ряд. После этого возьмем первые n1 предметов и поместим их в первую группу, вторые n2 предмета – во вторую группу, ..., последние nk предметов в k-ю группу. Ясно, что меняя положение предметов в ряду, можно получить всевозможные разбиения предметов. Так как число перестановок из n элементов равно n!, то число расположения предметов в ряд равно n! При этом заметим, что любая перестановка первых n1 предметов ничего не меняет, так же как и вторых n2, ..., и последних nk. В силу правила произведения получим n1!n2!...nk! перестановок предметов, не меняющих результата раздела. Таким образом, число способов разбиения на группы равно
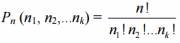
The formula matches the formula for the number of permutations with repetitions. You can come to the same result differently. The first n1 items are selected from n items. Since the order of the selected items is indifferent, it has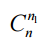 
choices. After this, the next n2 items are selected from the remaining n - n1. This can be done in 
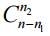ways, etc.
Finally, choose the last nk items from the remaining nk. This can be done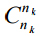 
, i.e. the only way. According to the work rule, we get that the number of ways of splitting into groups is equal to
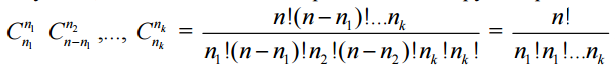
. As we see, the partitioning problems led to the already known combinatorial formulas.
Задача. 7 одинаковых шариков случайным образом рас- сыпаются по 4 лункам (в одну лунку может поместиться любое число шаров). Сколько существует различных способов распре- деления 7 шариков по 4 лункам?
Decision. Мы имеем 7 шариков, которые распределяем по 4 лункам (лунки могут быть пустые), т. е. это соответствует первой задаче о разбиениях, число способов равно 4^7 = 16348
Task. При игре в домино 4 игрока делят поровну 28 костей. Сколькими способами они могут это сделать?
Decision. Это задача о разделе 28 костей между 4 игрока- ми по 7 костей. Используя полученную выше формулу для числа способов такого раздела (задача 2), имеем
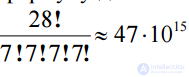
8. Рекомендации по решению задач
Решение комбинаторных задач представляет известную трудность для начинающих. Причин много, но одна из них очевидна – при изложении комбинаторики используется своя специфическая терминология (генеральная совокупность, выборка, правила выбора). В задаче же этих терминов, как правило, нет –сформулирована она на обычном литературном языке и комби-
наторные понятия присутствуют в ней в неявной форме. Поэтому после усвоения содержания задачи нужно ее «перевести»
на математический язык.
Для этого необходимо выяснить,
1) что является генеральной совокупностью - она всегда будет присутствовать в задаче, т. е. комбинаторные задачи свя-
заны с выбором объектов, а этот выбор из чего-то (генеральной совокупности) производится; каков объем генеральной сово-
купности;
2) одна или несколько генеральных совокупностей;
3) что является выборкой и каков объем выборки;
4) правила выбора: допустимы или нет повторы, важен ли порядок выбираемых элементов, возможно ли изменение состава.
После этого полезно для себя переформулировать задачу на языке генеральных совокупностей и выборок. В зависимости
от ситуации выбрать нужную формулу (см. таблицу). Иногда в более сложных задачах приходится использовать совместно не-
сколько формул.
В заключение приведем основные свойства чисел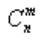 
.
Прежде всего, построим таблицу таких чисел, используя формулу (3.11).
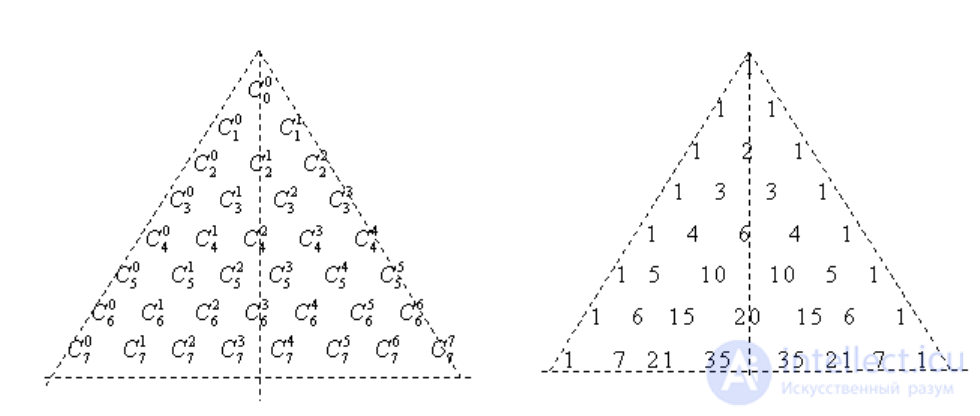
Таблица чисел 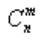имеет треугольную форму и называется треугольником Паскаля по имени математика Блеза Паскаля (1623-1662). Анализируя треугольник Паскаля, легко видеть основные свойства чисел .
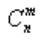Свойства 1 – 2 вытекают из определения сочетания как подмножества, содержащего m элементов множества, имеющего n элементов.
Properties 3 - 5 are proved by the method of mathematical induction.
By virtue of property 4, Pascal's triangle is easy to continue downwards by any number of steps.
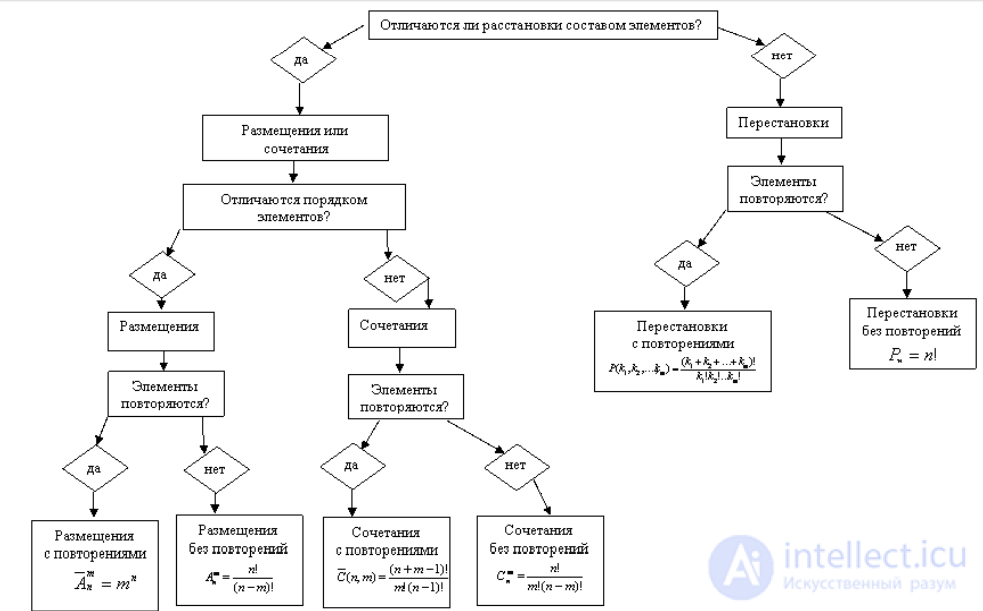
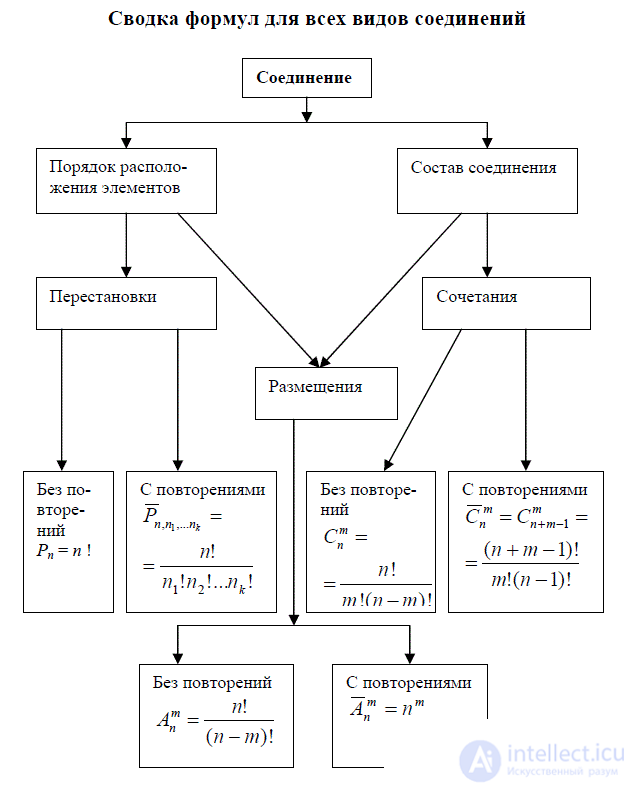
Figure 3.2 scheme for determining the type of arrangements and the choice of formulas
Еще подробнее про виды перестановок и примеры можно прочитать тут
https://intellect.icu/perestanovki-sochetaniya-i-razmeshheniya-s-i-bez-povtorenij-4268
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.