Lecture
A tree is a connected acyclic graph. [1] Connectivity means the presence of paths between any pair of vertices, acyclicity — the absence of cycles, and the fact that there is only one path between pairs of vertices.
A forest is an ordered set of ordered trees.
Oriented (directed) tree is an acyclic digraph (a directed graph that does not contain cycles), in which only one vertex has zero degree of entry (no arcs lead to it), and all other vertices have degree of entry 1 (they lead along exactly one arc ). A node with a zero degree of entry is called the root of a tree, and peaks with a zero degree of outcome (from which no arc comes) are called terminal vertices or leaves . [2]
The root tree is a tree in which one vertex is selected (the root of the tree). Formally, the root tree is defined as a finite set 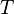 one or more nodes with the following properties:
one or more nodes with the following properties:
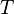
 disjoint sets
disjoint sets 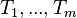 , and each of the sets is a root tree; trees
, and each of the sets is a root tree; trees 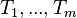 are called subtrees of this root
are called subtrees of this root 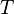
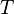 equals 0;
equals 0;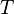 containing this node.
containing this node.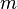 tier wood
tier wood 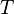 - many tree nodes, at the level
- many tree nodes, at the level 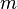 from the root of the tree.
from the root of the tree.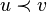 if vertices
if vertices 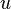 and
and 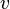 different and top
different and top 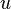 lies on the (unique!) elementary chain connecting the root to the vertex
lies on the (unique!) elementary chain connecting the root to the vertex 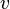 .
.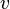 - subgraph
- subgraph 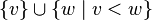 .
.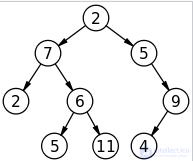
A simple binary tree of size 9 and height 3, with a root of value 2. This tree is not balanced and not sorted.
The term binary tree (it is also a binary tree ) has several meanings:
N-ary trees are defined by analogy with a binary tree. For them, there are also oriented and non-oriented cases, as well as corresponding abstract data structures.
 vertices contains
vertices contains 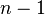 edge. Moreover, a finite connected graph is a tree if and only if
edge. Moreover, a finite connected graph is a tree if and only if 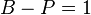 where
where 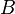 - the number of vertices
- the number of vertices 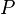 - the number of edges of the graph.
- the number of edges of the graph.Main article: Cayley's theorem on the number of trees
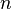 numbered vertices equal to
numbered vertices equal to 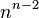 ( Cayley's theorem [3] ).
( Cayley's theorem [3] ).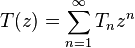
for the number 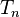 nonisomorphic rooted trees with
nonisomorphic rooted trees with 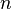 vertices satisfies the functional equation
vertices satisfies the functional equation
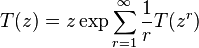 .
.
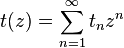
for the number 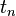 non-isomorphic trees with
non-isomorphic trees with 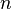 vertices can be represented using the enumeration series for root trees:
vertices can be represented using the enumeration series for root trees:
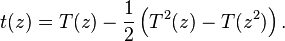
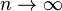 the following asymptotics is true
the following asymptotics is true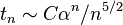
Where 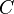 and
and 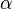 certain constants
certain constants 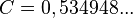 ,
, 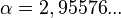 .
.
The tree can be encoded with sets of zeros and ones. Consider, for example, laying wood on a plane. Starting from any vertex, we move along the edges of the tree, turning at each vertex to the nearest edge to the right and turning back at the terminal vertices of the tree. Passing along some edge, we write 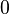 when moving along the edge for the first time and
when moving along the edge for the first time and 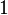 when moving along the edge a second time (in the opposite direction). If a
when moving along the edge a second time (in the opposite direction). If a 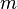 - the number of edges of the tree, then through
- the number of edges of the tree, then through 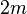 steps we will return to the original vertex, passing along each edge twice. The resulting sequence from
steps we will return to the original vertex, passing along each edge twice. The resulting sequence from 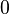 and
and 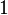 (tree code) length
(tree code) length 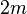 allows you to uniquely recover not only the tree itself
allows you to uniquely recover not only the tree itself 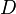 but its laying on the plane. Arbitrary tree correspond to several such codes. In particular, the following rough estimate for the number of trees with
but its laying on the plane. Arbitrary tree correspond to several such codes. In particular, the following rough estimate for the number of trees with 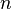 tops:
tops:
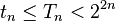
Такая кодировка мне понятна, доступна. Учусь кодить. Пишу html графы деревьев.
что значит html графы ?
https://code.sololearn.com/WZTTXNB4wCy1/?ref=app
Наверное, правильнее сказать не графы, а схемы деревьев.
Да, существует большое количество библиотек для визуализации графов,
а вообще т.к понятие граф растяжимое в прямом смысле (один и тот же граф можно изобразить -
визуализировать бесконечным количесвтом образов),
существуют специальные теории и алгоритмы визуализации графов,
например можно прочитать тут
https://intellect.icu/sposoby-vizualizatsii-grafov-silovye-algoritmy-vizualizatsii-grafov-9034
еще есть даже Non-SQL для работы с графами в том числе с визуализацией
вот пример такой БД
http://console.neo4j.org/
https://neo4j.com/
Визуализация гибкого force-directed графа осуществляется с использованием метода численного интегрирования Верле библиотека JS https://github.com/d3/d3
библиотека https://www.graphviz.org/
и другие
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.