Lecture
The path in the graph is a sequence of vertices having an edge for each vertex connecting it with the next vertex in the sequence.
Let G be an undirected graph. The path in G is such a finite or infinite sequence of edges and vertices [1]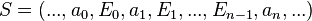 
,
that every two adjacent edges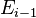 
and 
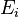have a common top 
.
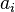So you can write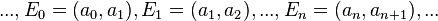 
Note that the same edge can occur on the path several times. If there are no edges preceding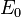 
then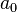 
is called the initial vertex S, and if there are no edges following 
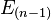then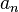 
is called a finite vertex of S. Any vertex belonging to two adjacent edges is called inner. Since the edges and vertices in the path can be repeated, the inner vertex can be the starting or ending vertex.
If the initial and final vertices coincide, the path is called cyclic. A path is called a chain, and a cyclic path is called a cycle if each edge of the path occurs no more than once (vertices can be repeated). A non-cyclic chain is called a simple chain if no vertex repeats in it. Loop with the end 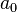called a simple cycle if 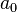It is not an intermediate vertex in it and no other vertices are repeated.
Unfortunately, this terminology is not settled. Wilson [2] writes: “What we called the route is also called the path, the edge sequence. A chain is called a path, a semi-simple path; simple chain - by chain, by way, by arc, by simple way, by elementary chain; closed circuit - cyclic circuit, contour; cycle - by contour, contour circuit, simple cycle, elementary cycle. " [3] [4] [5]
Oriented cycle. Without arrows, it's just a cycle. This is not an easy loop, because the blue vertices are used twice.
Ways, chains and cycles are fundamental concepts of graph theory and are defined in the introductory part of most books on graph theory. See, for example, Bondy and Marty (Bondy, Murty, 1976), Gibbons (Gibbons, 1985), or Distel (2005).
The path for which no edges of the graph connect two vertices of the path is called an induced path.
A simple chain containing all the vertices of the graph without repetition is known as the Hamiltonian path.
A simple cycle containing all the vertices of a graph without repetitions is known as the Hamiltonian cycle.
The cycle obtained by adding a graph edge to the spanning tree of the original graph is known as the Fundamental cycle.
Two paths are vertex independent if they do not have common internal vertices. Similarly, two paths are edge-independent if they do not have common internal edges.
The length of the path is the number of edges used along the path, with reusable edges being counted the corresponding number of times. The length can be zero if the path consists of only one vertex.
A weighted graph assigns a certain value ( edge weight ) to each edge. The weight of the path in a weighted graph is the sum of the weights of the edges of the path. Sometimes, instead of the word weight , price or length is used .
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.