Splitting set. Sets of sets. Classification. Breaking up into classes. Examples

A partition of a set is its representation in the form of a union of an arbitrary number of pairwise disjoint subsets.

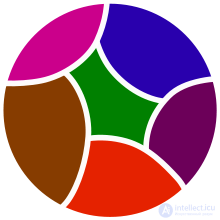
Figure 1 is an example of partitioning a set.

Definition

Let be 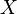- arbitrary set. Family of nonempty sets 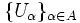where 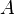- some set of indices (finite or infinite), is called a partition 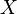, if a:

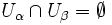1. for any 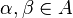such that ;
2. .

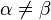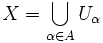With this set 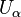are called blocks or parts of a partition of a given set .

Partitioning of finite sets

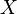Partitions of finite sets, as well as counting the number of different partitions that satisfy one or another condition, are of particular interest in laboratory work. In particular, some combinatorial functions naturally arise as a number of partitions of one kind or another.

For example, the Stirling number of the second kind 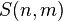is the number of unordered partitions of an n- element set into m parts, while the multinomial coefficient 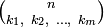Express the number of ordered partitions of an n- element set into m parts of fixed size 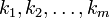. The number of all unordered partitions of an n -element set is given by the Bell number .

Examples

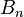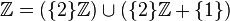• where 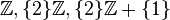- sets of all integers, even integers and odd integers, respectively;
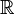• The set of all real numbers can be represented as: ;
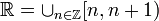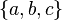• Many of the three elements can be broken down in five ways: 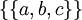, , 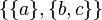, , 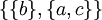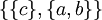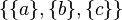- Bella number .

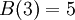Examples of Sets of sets. We can consider sets consisting of the most various elements. In particular, we can consider sets of sets, that is, sets, whose elements are the essence of a set. Such, for example, is the set of all pairs of oars available at this boat station. The set of sets is also the set of all sports teams of the city of N. (each sports team is a set of its athletes).

The set of all trade unions, as well as the set of all military units (divisions, regiments, battalions, companies, platoons, etc.) of a given army are sets of sets. These examples show that sets that are elements of a given set of sets can intersect in some cases, in other cases, on the contrary, they do not have common elements.

For example, the set of all parties in a country is a set of mutually disjoint sets, since a citizen cannot be a member of two political parties at the same time. On the other hand, the set of all military units of an army is an example of a set of sets, some elements of which are subsets of other elements: so, each platoon is a subset of a certain regiment, a regiment is a subset of a division, etc.

Many sports teams of a given city consist, generally speaking, of overlapping sets, since the same person can belong to several sports teams (for example, a swimmers team and a volleyball or skier team).

Comment. To facilitate speech, sometimes instead of the expression “set of sets” are used as the absolutely equivalent expressions “set system” or “set of sets”.

The concept of partitioning sets into classes

The concept of a set and operations on sets makes it possible to clarify the concept of classification.

Classification is the action of distributing objects into classes based on the similarities within the class and how they differ from other objects. The classification is widely used in mathematics.

For example, natural numbers are divided into even and odd; angles are sharp, obtuse and straight, etc.

Any classification is associated with the splitting of a certain set of objects into subsets.

Consider that the set X is divided into classes X X , ..., X 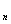, if a:

1) subsets of 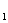X X 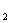, ..., X 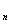do not intersect in pairs;

2) the union of these subsets coincides with the set X.

If at least one of these conditions is not met, the classification is considered incorrect.

For example: a) The set of triangles X is divided into three classes: acute-angled, rectangular and obtuse-angled. Indeed, the selected subsets do not overlap in pairs, and their union coincides with the set X; b) From the set of triangles X identified subsets of isosceles, equilateral and versatile triangles. Since the sets of isosceles and equilateral triangles intersect, this means that the first classification condition is not fulfilled, and we have not received a partition of the set X into classes.

Since the partition of a set into classes is associated with the allocation of its subsets, the classification can be performed using the properties of the elements of the sets.

Consider, for example, the set of natural numbers. Its elements have different properties. We are interested in numbers with the "be a multiple of 3 " property. This property allows you to select from the set N a subset consisting of multiples of 3 . Then about the other natural numbers, we can say that they are not a multiple of 3 , i.e. we get another subset of the set N. Since the selected subsets do not overlap, and their union coincides with the set N , we have a partition of this set into two classes.

In general, if one property is given on the set X , then this set is divided into two classes. The first is a class of objects with this property, and the second is the addition of the first class to the set X. The second class contains such objects of the set X that do not possess the specified property. This classification is called dichotomous.

Consider the situation when two properties are set for the elements of a set. For example, the properties of natural numbers: “be a multiple of 3” and “be a multiple of 5”. Using these properties, we can distinguish two subsets from the set N : A is a set of numbers that are multiples of 3 and B is a set of numbers that are multiples of 5. These sets intersect, but none of them is a subset of the other (Fig. 13). Partitions into subsets A and B in this case did not occur. But a circle representing the set N can be considered as consisting of four non-intersecting regions. Each region represents some subset of N. The set I consists of numbers that are multiples of 3 and 5, the set I is from numbers that are multiples of 3 and not multiples of 5, the set of III is from numbers that are multiples of 5 and not multiples of 3, the set of IV is from numbers that are not multiples of 3 and not multiples of 5 The union of these four sets is the set N.

Thus, the selection of two properties led to the division of the set N of natural numbers into four classes.

One should not think that setting two properties of the elements of a set always leads to splitting this set into four classes. For example, using these two properties “to be a multiple of 3” and “to be a multiple of 6”, the set of natural numbers is broken

into three classes (fig. 14): I is a class of multiples of 6; II - class of multiples of 3, but not multiples of 6; III - a class of numbers not multiples of 3.

examples of division into classes. A very important class of set systems is obtained if we consider all possible partitions of a set into mutually non-intersecting sets. Given the set X, represented as a sum of pairwise disjoint subsets; the sets that add up to our sum are elements of a given partition of the set X.

Example 1. M is the set of all students in secondary schools in Moscow. The set M can be divided into pairwise non-intersecting subsets, for example, in the following two ways:

1) we combine all pupils of the same school in one term (i.e., we divide the set of all pupils by schools);

2) we unite all pupils of the same class (albeit from different schools) into one term.

Example 2. Let X be the set of all points of the plane; take some straight line g on this plane and divide the whole plane into straight lines parallel to the line g. The sets of points of each such line are the subsets into which we divide the set X.

If a given set X is divided into pairwise disjoint subsets, giving a total set of M, then, for brevity, they simply say that the set M is divided into classes