Lecture
Binary tree is a hierarchical data structure in which each node has no more than two descendants (children). As a rule, the first is called the parent node, and children are called left and right heirs.
For practical purposes, two subspecies of binary trees are commonly used — the binary search tree and the binary heap.
There is the following recursive definition of a binary tree (see BNF):
:: = ( ) | nil.
That is, a binary tree is either empty or consists of data and two subtrees (each of which may be empty). An obvious but important fact to understand is that each subtree in turn is also a tree. If a node has both subtrees empty, then it is called a leaf node (leaf vertex) or a terminal element.
For example, shown on the right in fig. 1 tree, according to this grammar could be written as:
(m
(e
(c
(a nil nil)
nil
)
(g
nil
(k nil nil)
)
)
(s
(p (o nil nil) (s nil nil))
(y nil nil)
)
)
|
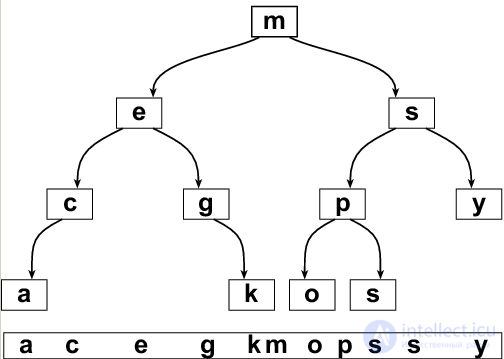
Fig. 1. Binary search tree, in which the keys are Latin characters ordered alphabetically. |
Each node in the tree defines a subtree , the root of which it is. The vertex m = (data, left, right) has two children (left and right) left and right and, accordingly, two subtrees (left and right) with left and right roots.
Many useful data structures are based on a binary tree:
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.