Multigraph and pseudograph

Multigraph with multiple edges (red) and loops (blue). Not all authors allow multigraphs to have loops.

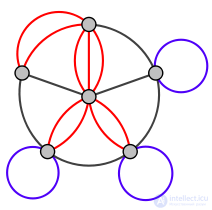
In graph theory, a multigraph (or pseudograph ) is a graph in which the presence of multiple edges is allowed ^[en] (they are also called “parallel” ^[1] ), that is, edges that have the same finite vertices. Thus, two vertices can be connected by more than one edge. (Thus, multigraphs differ from hypergraphs, in which each edge can connect any number of vertices, and not exactly two.)

Pseudograph - a graph in which there are loops and / or multiple edges.

Multigraph - pseudograph without loops.

There are two different ways to label edges of a multigraph. Some say that, as in the case of graphs without multiple edges, the edge is determined by the vertices it connects, but each edge can be repeated several times. Others define edges equal to the vertices of the elements of the graph, and they must have their own identification.

Non-oriented multigraphs (edges without self-identification)

Formally, a multigraph G is an ordered pair G : = ( V , E ), in which

• V is the set of vertices ,
• E is a multiset of unordered pairs of vertices. The elements of this set are called edges .

Multigraphs can be used to represent the possible air paths of an airplane. In this case, the multigraph becomes oriented, and a pair of oriented parallel edges connecting the cities shows that it is possible to fly in both directions - from the city, or into the city.

Some authors allow multigraphs to have loops, that is, edges connecting a vertex to it, ^[2] while others call such graphs pseudographs , leaving the term multigraph to graphs without loops. ^[3]

Oriented multigraphs (edges without self-identification)

A multi -graph is a directed graph in which multiple arcs are allowed, that is, arcs that have the same starting and ending vertices. A multi-graph G is an ordered pair G : = ( V , A ), in which

• V is the set of vertices ,
• A is a multiset of ordered pairs of vertices. The elements of this set are called arcs .

The mixed multigraph G : = ( V , E , A ) can be defined in the same way as the mixed graph ^[en] .

Oriented multigraphs (edges with own identification)

A multi-map (or quiver ^[en] ) G is called an ordered quadruple G : = ( V , A , s , t ), in which

• V is the set of vertices ,
• A is the set of arcs ,
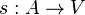• assigns each arc a starting vertex
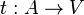• assigns each arc a final vertex.

In the theory of categories, small categories can be defined as multi-graphs (with arcs having their own identity), equipped with the law of construction and loops for each vertex, serving as left and right identification for the construction. For these reasons, in the theory of categories, the term graph is usually understood as a “multi-organ” and the underlying multi- organ of the category is called the base digraph .

Markup

Multigraphs and multi-graphs support the notion of markup in the same way. However, in this case there is no unity of terminology.

The definitions of tagged multigraphs and tagged multi-graphs are similar, so here we will define only for multi-graph.

Definition 1 : A multiformat labeled is a labeled ^[en] graph with labels on arcs and vertices.

Formally: The labeled multi-corporation G is a tuple of 8 elements 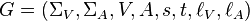, wherein

• V is the set of vertices and A is the set of arcs
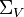• and 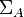- the final alphabet available for marking arcs and vertices,
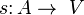• and 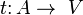- two mappings defining the initial and final vertices of the arc,
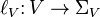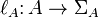• and - two mappings describing the layout of vertices and arcs.

Definition 2 : Marked multi-digraph is a tagged ^[en] digraph with multiple marked arcs, that is, arcs with the same ends and the same labels (note that this is different from the concept given in the article “Markup of the graph ^[en] ”).

See also

• Glossary of graph theory
• Graph theory