Lecture
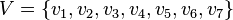 ,
, 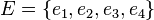
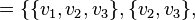
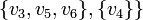 .
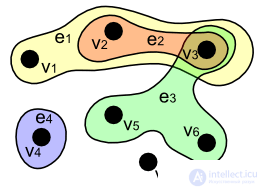
. A hypergraph is a generalization of a graph in which not only two vertices, but also any subsets of vertices can be connected with each edge.
From a mathematical point of view, a hypergraph is a pair 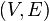 where
where 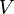 - non-empty set of objects of some nature, called the vertices of the hypergraph, and
- non-empty set of objects of some nature, called the vertices of the hypergraph, and 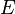 - family of non-empty (not necessarily different) subsets of the set
- family of non-empty (not necessarily different) subsets of the set 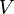 called the edges of the hypergraph.
called the edges of the hypergraph.
Hypergraphs are used, in particular, when modeling electrical circuits.
The transversal of a hypergraph is a set 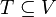 containing a non-empty intersection with each edge. Such a transversal will be minimal if none of its subsets are themselves a transversal of the hypergraph.
containing a non-empty intersection with each edge. Such a transversal will be minimal if none of its subsets are themselves a transversal of the hypergraph.
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.