Lecture
I want to say right away that there is no water here about the Hasse diagram, and only the necessary information. In order to better understand what the Hasse diagram is, I strongly recommend reading everything from the category Discrete Mathematics. Set Theory. Graph Theory. Combinatorics .
A Hasse diagram is a type of diagram used to represent a finite partially ordered set as a drawing of its transitive reduction. Specifically, for a partially ordered set,
the diagram represents each element
as vertices in the plane and line segments or curves going up from element
to element
if
and there is no element
for which
. These curves may intersect but need not pass through vertices unless they are the endpoints of a line. Such a diagram, with labeled vertices, uniquely defines the partial order.
This type of visualization was first described systematically by Birkhoff in 1948 , and he also gave it the name in honor of Helmut Hasse, who used similar diagrams, but such drawings are also found in earlier works, for example, in the textbook of the French mathematician Henri Vogt (German: Henri Vogt) published in 1895 .
Any partially ordered set can be represented as a diagram in which each element is represented by a point on the plane. If an element y covers an element x, then x and y are connected by a segment, with the point x located below the point y. Such diagrams are called Hasse diagrams.
Element y covers element x:
Let A ≠ ∅ and card A < ∞. Let p (a subset of A 2 ) be an order relation. An element y covers an element x if y ≤ x and there is no u ∈ A (x < u < y).
Partial order relations, i.e. reflexive, antisymmetric and transitive relations, to which a number of additional properties are imposed, are studied within the framework of the section of mathematics with the exotic name of LATTICE THEORY. This name is frightening, therefore in our country the word lattice was initially translated as "structure". But when the term structure began to be used more and more widely in mathematics, it had to be given the Russian word строительства, and lattices became lattices in our country too.
It can be assumed that the name "lattices" arose in connection with the use of the so-called Hasse diagrams3, which resemble extravagant window grilles...
Let's start with examples of lattices.
Let's take the words: о, ор, вор, ворот, коль, олово, кольово - and order them by the occurrence of some words in others (not forgetting that each word is included in itself). This will be our first lattice.
We can see that all the properties of partial order are fulfilled here. And we will talk about additional properties later.
Numbers: 1, 2, 3, 4, 6, 9, 12, 18, 36 with the relation "divide evenly" also form a lattice.
Ordinary real numbers with the relation "greater than or equal to" give one of the most common lattices. Although for us it is less exotic. One could say, simple as a log...
The set of all subsets of some set with the relation of inclusion gives a lattice, and, moreover, with a number of remarkable properties.
Relations similar to order relations, but not possessing the property of transitivity, are called TOLERANCE relations.
A good illustration of this relation are many famous pictures by Escher, where, for example, birds smoothly turn into fish, etc.
Although Hasse diagrams are a simple and intuitive tool for working with finite partially ordered sets, it is very difficult to draw a "good" visual diagram for a sufficiently non-trivial set due to the large number of possible representations. The simple technique of starting with the smallest elements and drawing the elements above it in sequence often gives poor results - symmetries and internal structures are easily lost.
For example, the power set of a set of four elements ordered by the inclusion operation 
can be represented by any of the four diagrams below (each subset is labeled with a binary encoding indicating whether the corresponding element is contained in the subset - 1, or not - 0):
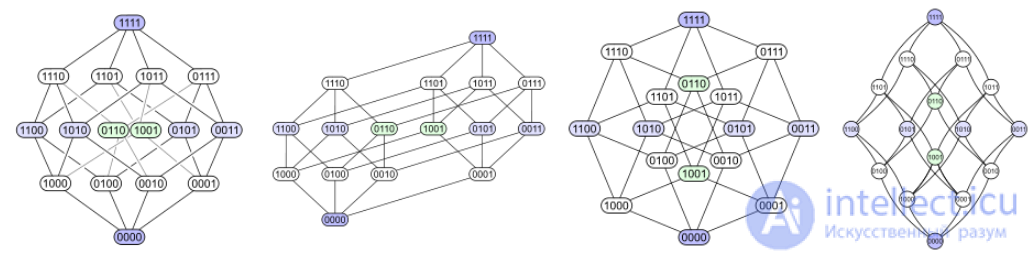
The first diagram shows the level structure. The second diagram has the same level structure, but some edges are extended to emphasize that the four-dimensional cube is the union of two three-dimensional cubes. The third diagram shows some internal symmetry. In the fourth diagram, the vertices are arranged like a 4×4 matrix.
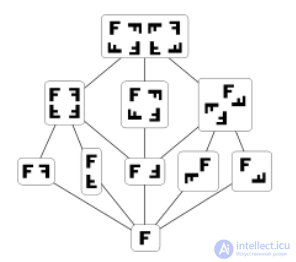
The Hasse diagram of the subgroup lattice of the dihedral group 
has no intersecting edges.
Some properties of partial orders with respect to the planarity of their Hasse diagram (that is, the possibility of drawing it without crossing edges):
the -coordinates of elements of a partial order are given, then its Hasse diagram can be found in linear time that preserves the given coordinates, if such a diagram exists . In particular, if a partial order has levels, one can determine in linear time whether there is a Hasse diagram without crossings in which the height of each vertex is proportional to its rank.The Greatest (Largest) and the Smallest Element. The smallest element of the diagram is the element that begins the diagram, and the largest (greatest) is the element that ends it. Moreover, if there are several largest (greatest) or smallest elements, then the answer will be that there is no largest or smallest element. In other words, the largest (greatest) and smallest element on the Hasse diagram is only one.
Returning to the first example, it is immediately clear that the smallest element will be Ø, and the largest (greatest) {3;6;4}. This is stated on the website https://intellect.icu . In the second example, the smallest element will be 1, and there will be no largest (greatest) element, since the largest (greatest) elements can be both 4 and 10, therefore, there is no largest (greatest) element in the second example.
Maximal elements are those that are not replaced by another element. Minimal elements are those that are not preceded by another element.
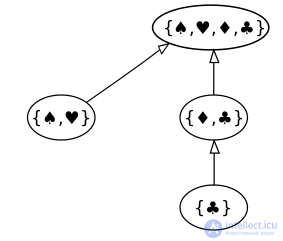
Expressing an example using standard UML inheritance connectors. Each set is a separate object (standard UML blocks are rectangular).
The standard diagram for a containment chain is a UML class that links sets by an inheritance relationship. The figure shows a nested collection set, C :
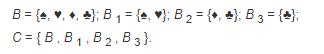
In software engineering, the classes of a software system and the inheritance relationships between those classes are often depicted using a class diagram, a form of the Hasse diagram in which the edges connecting classes are drawn as solid line segments with an open triangle at the superclass end.
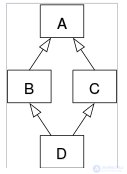
Class diagram depicting multiple inheritance
example 1
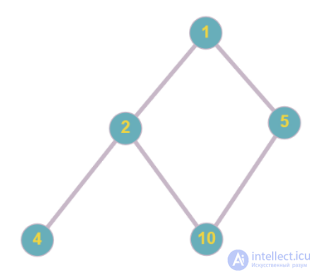
Fig.1 Hasse diagram for the second relation
Let us construct a Hasse diagram for the relation Ω, where Ω: is a divisor.
Let us take the set A = {1;2;4;5;10}. The constructed diagram is shown in Fig. 1.
example 2
Let us take some set A = {3;6;4} and construct a relation ƿ, where ƿ: P(A) x P(A). P(A) is the set of all subsets, it can be represented as follows: { Ø, {3}, {6}, {4}, {3;6}, {6;4}, {3;4}, {3;6;4}}. Let us construct the Hasse diagram of this relation. Figure 2 shows this diagram.
Note that in this diagram one element “Covers” the other, that is, if we take two random elements, they are not equal to each other and one of these elements precedes the other. For example, let's take from the diagram the element Ø and {3}, they are not equal to each other and one precedes the other.
Another property of the Hasse diagram is that from any part of the diagram you can get to any other
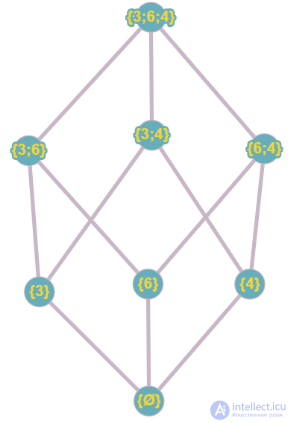
Fig.2 Hasse diagram for the relation
example 3
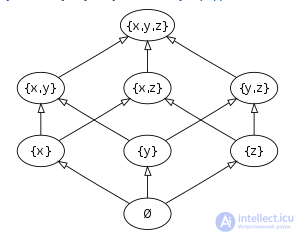
Boolean ( English power set , German potenzmenge ) - in set theory , this is the set of all subsets of a given set , is reflected or (since it corresponds to the set of reflections with in ).
The Boolean of { x , y , z } is partially ordered by inclusion :
The set A = {1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60} of all divisors of 60 is partially ordered by divisibility :
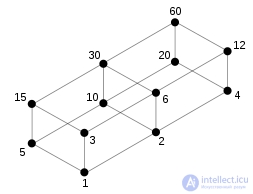
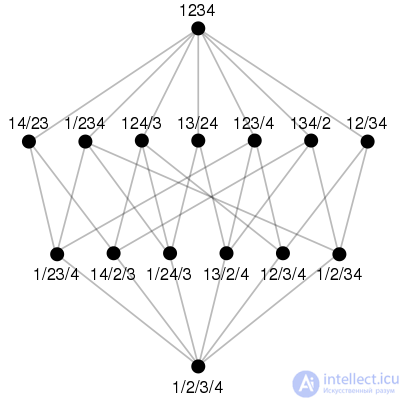
The set of all 15 partitions of the set { 1, 2, 3, 4 }, where the coarser partition is higher than the finer one:
The Hasse diagram has wide application in various fields, especially in the theory of partially ordered sets. Here are some examples of the application of the Hasse diagram:
Lattice Theory: Hasse diagrams are widely used in lattice theory to study and visualize the structure of lattices and their properties. They allow one to visualize the order relationship and the structure of elements in a lattice.
Taxonomy and Classification: Hasse diagrams are often used in taxonomy and classification to organize and visualize the relationships between different categories or classes. They help to understand the hierarchical structure and relationships between different concepts.
Data Analysis: In data analysis, Hasse diagrams can be used to visualize hierarchies or hierarchical relationships between data or variables. They can help researchers better understand the structure of data and its relationships.
Logic and Algebra: Hasse diagrams also find application in logic and algebra. They are used to visualize and study the structure of algebraic systems such as Boolean algebras and set algebras.
Exploring Order: Hasse diagrams are a powerful tool for exploring order relations and properties of partially ordered sets. They reveal minimal and maximal elements, chains, antichains, and other structural properties.
These are just a few examples of the application of the Hasse diagram. Its flexibility and intuitive clarity make it a useful tool in various fields where it is necessary to visualize and analyze the structure and relationships between elements.
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.