Lecture
The subfactorial of the number n (symbol :! N ) is defined as the number of disorders of order n , that is, permutations of order n without fixed points. The name of the subfactorial comes from the analogy with factorial, which determines the total number of permutations.
In particular ,! N is the number of ways to put n letters in n envelopes (one in each), so that no one gets into the corresponding envelope (the so-called Letter Problem).
The subfactorial can be calculated using the inclusion-exclusion principle:
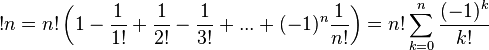
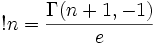 where
where 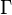 denotes an incomplete gamma function ( English ), and e is a mathematical constant;
denotes an incomplete gamma function ( English ), and e is a mathematical constant;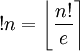 where
where 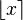 denotes the integer closest to x .
denotes the integer closest to x .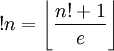 (according to Mehdi Hassani ) where
(according to Mehdi Hassani ) where  denotes the integer part of a number.
denotes the integer part of a number.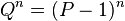 and
and 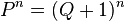 where
where 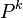 need to understand how
need to understand how 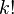 , but
, but 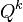 - as
- as 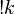 .
.! 1 = 0
! 2 = 1
! 3 = 2
! 4 = 9
! 5 = 44
! 6 = 265
! 7 = 1 854
! 8 = 14,833
! 9 = 133 496
! 10 = 1,334,961
! 11 = 14,684,570
! 12 = 176 214 841
! 13 = 2 290 792 932
! 14 = 32 071 101 049
! 15 = 481 066 515 734
! 16 = 7 697 064 251 745
! 17 = 130,850,092,279,664
! 18 = 2 355 301 661 033 953
! 19 = 44 750 731 559 645 106
! 20 = 895 014 631 192 902 121
! 21 = 18,795,307 255,050,944,540
sequence A000166 in OEIS
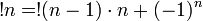
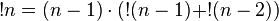 (factorial has the same property)
(factorial has the same property)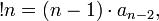
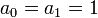 and
and 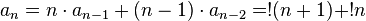 . Initial members of the sequence
. Initial members of the sequence 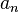 :
:
1, 1, 3, 11, 53, 309, 2119, ... (sequence A000255 in OEIS)
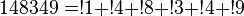 (found JS Madachy, 1979)
(found JS Madachy, 1979)
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.