Numerical characteristics of graphs Chromatic number of graphs

The chromatic number of the graph G is the minimum number of colors in which you can color the vertices of the graph G so that the ends of any edge have different colors. Denoted by χ ( G ).

Definition

Chromatic number of the graph - the minimum number 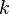such a lot 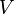vertices of the graph can be divided into 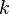disjoint classes :

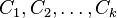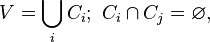
such that the vertices in each class are independent, that is, any edge of the graph does not connect the vertices of the same class.

Related definitions

• K-colored graph is a graph whose chromatic number does not exceed . That is, its vertices can be painted different colors so that any edges will have different colors.
• K-chromatic graph - a graph whose chromatic number is equal to . That is, the vertices of the graph can be painted 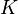colors so that at any edge the ends will be of different colors, but so color 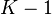Flowers - no longer possible.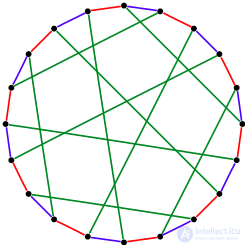

Ribbed coloring

графа Дезарга.

line coloring cubic graph

The chromatic class of the graph G is the minimum number of colors in which the edges of the graph G can be colored so that the adjacent edges have different colors. Denoted by χ '( G ). The problem of edge coloring of an arbitrary flat cubic graph without bridges in three colors is equivalent to the famous Problem of four colors. The edge coloring determines the 1-factorization of the graph.

Chromatic polynomia

If we consider the number of different colorings of the labeled graph as a function of the available number of colors t , then it turns out that this function will always be a polynomial in t . This fact was discovered by Birkhoff and Lewis [1] while trying to prove the hypothesis of four colors.

Chromatic polynomials of some graphs

Triangle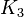
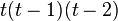Complete graph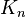
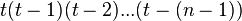Tree with tops
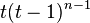Cycle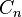
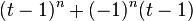Count Petersen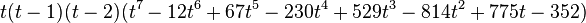

Finding the chromatic polynomial of an arbitrary graph [edit]

For a vertex graph, the chromatic polynomial is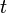

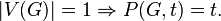
The chromatic polynomial of a graph is equal to the product of chromatic polynomials of its components.

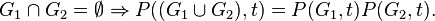
There is also a recurrence relation.

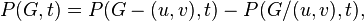
Where 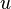and 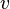- adjacent vertices, 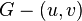- graph resulting from graph 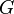by removing the edge 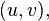but 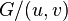- graph resulting from graph 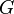by tightening the rib 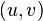exactly.
You can use the equivalent formula

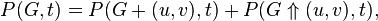
Where 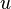and 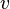- non-adjacent vertices, and 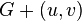- graph resulting from graph 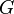by adding an edge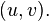

Properties of the chromatic polynomial [edit]

For all positive integers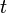

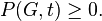
Chromatic number 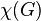- the smallest positive integer 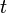, for which

Generalizations [edit]

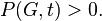
Also, the chromatic number can be considered for other objects, for example, for metric spaces. Thus, the chromatic number of a plane is the minimum number of colors χ for which there exists such a coloring of all points of the plane into one of the colors that no two points of the same color are exactly 1 apart from each other. Similarly for any dimension of space. It is elementarily proved that for a plane 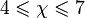however, it is still not possible to advance further. This task is called the Nelson – Erdёs – Hadwiger problem.

Implications for graph theory

Many deep problems of graph theory are easily formulated in terms of coloring. The most famous of these problems, the problem of four colors, has now been solved, but new ones are emerging, for example, a generalization of the problem of four colors, the Hadwiger hypothesis.

See also

• Practical application of graph coloring
• Combination

Notes

1. ↑ Birkhoff, GD and Lewis, DC “Chromatic Polynomials.” Trans. Amer. Math Soc. 60, 355–451, 1946.

Literature

• O. Ore. Graph theory. Translated from English by I. N. Vrublevskaya, edited by N. N. Vorobyova. M .: Science, 1986.