Relationship tolerance

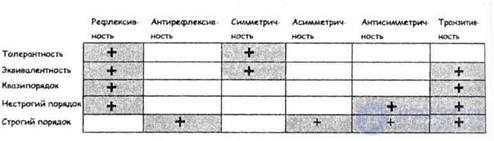
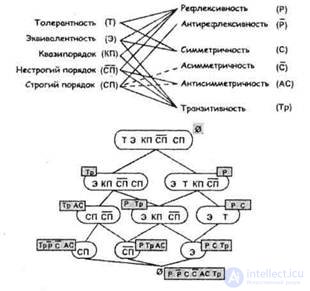
The relation of tolerance (or simply tolerance) on the set 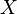is called a binary relation that satisfies the properties of reflexivity and symmetry, but is not necessarily transitive. Thus, the equivalence relation is a special case of tolerance.

In contrast to the equivalence relation, which divides the set of elements on which it is defined into disjoint subsets, the tolerance relation provides coverage for this set. The relationship of tolerance is used, for example, also in classifying information in knowledge bases. ^[one]

Meaning of the term at a meaningful level

At a meaningful level, tolerance means the following. Any object is indistinguishable with itself (the reflexivity property), and the similarity of two objects does not depend on the order in which they are compared (the symmetry property). However, if one object is similar to another, and this other one is similar to the third, this does not mean at all that all three objects are similar to each other (thus, the transitivity property may not hold).

The relationship of tolerance is often used to describe the relationship of similarity between real objects, relationships of acquaintance or friendship between people. In all these cases, the transitivity property is not supposed to necessarily be fulfilled. In fact, Ivanov may be familiar with Petrov, Petrov - with Sidorov, but at the same time Ivanov and Sidorov may not be familiar with each other.

A relationship on a set of words will also be tolerant, in which it is defined as having at least one common letter. In this case, for example, the crossword words of a crossword are in relation. ^[2]

Consider examples where tolerance is defined in different ways.

Example 1: The set M consists of four-letter Russian words - common nouns in the nominative case. We will call such words similar if they differ by no more than one letter. The well-known problem "The transformation of a fly into an elephant" is formulated in precise terms as follows. Find the sequence of words beginning with the word "fly" and ending with the word "elephant", any two adjacent words in which are similar in the sense of the definition just given. The solution to this problem:

fly - mura - tour - tara - kara - kare - cafe - kafr - kayur - kayuk - hook - croc - term - runoff - moan - elephant.

Example. The set M consists of four-letter Russian words - common nouns in the nominative case. We will call such words similar if they differ by no more than one letter. The well-known problem “Turning a fly into an elephant” is formulated in precise terms as follows:

Find such a sequence of words, beginning with the word "fly" and ending with the word "elephant", any two adjacent words in which are similar (in the sense of the definition just given).

We will give a solution to this problem: Fly - Mura - Tura - Tara - Kara - Kare - Cafe - Kafir - Kayur - Kayuk - Hook - Croc - Term - Drain - Moan - Elephant.

At a meaningful level, tolerance means the following. Any object is indistinguishable from itself (reflexivity property), and the similarity of two objects does not depend on the order in which they are compared (symmetry property). However, if one object is similar to another, and this other one is similar to the third, this does not mean at all that all three objects are similar to each other (thus, the transitivity property may not hold).

The relationship of tolerance is often used to describe the relationship of similarity between real objects, relationships of acquaintance or friendship between people. In all these cases, the transitivity property is not supposed to necessarily be fulfilled. In fact, Ivanov may be familiar with Petrov, Petrov - with Sidorov, but at the same time Ivanov and Sidorov may not be familiar with each other.