Lecture
Regular graph
Regular graph
a graph whose degrees of all vertices are equal; the degree of its vertices is called the degree of a regular graph. All full graphs are regular; graphs of platonic bodies are also regular. A regular graph of degree n is an n- dimensional cube. Another name is Homogeneous graph.
A homogeneous graph is a graph in which all vertices have the same degree. [one]
Theorem 7.5.1. Homogeneous graph has no deficiency. [2]
Theorem 7.5.3. An almost homogeneous graph G , in which the deviations defined in (7.5.6) satisfy conditions (7.5.8), has a homogeneous first-degree subgraph. [3]
If O is a homogeneous graph , then it is recovered. [four]
The greatest complexity is the establishment of an isomorphism of homogeneous graphs with automorphic subgraphs. To solve such problems, methods are used to partition the graphs under study into various levels. [five]
In fig. 1.2.2 shows examples of two infinite homogeneous graphs . [6]
The requirement that the graph has a given group does not impose significant restrictions on its other properties. Izbitsky and Sabidussi showed that it is possible to find a homogeneous graph with an arbitrary degree, connectivity, chromatic number and other characteristics. [7]
Note that an ordinary complete graph with k vertices is (k - 1) - homogeneous. It can also be noted that, according to Theorem 1.3, a homogeneous graph has an even number of vertices if k is odd.
If for all vertices d (v) = k, then the graph is called a homogeneous graph of degree k or k-homogeneous. The graph in fig. 10.21.5 is complete and 3-uniform.
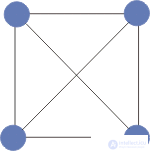
Fig. 10.21.5.
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.