Lecture
Let A be a binary relation in the set X. We define the general properties of such relations that must be satisfied for all pairs ( Xi , Xj ) Î A.
· Reflexivity.
The relation A is reflexive if A É E ( E is the identity relation), i.e. it always holds between the object and itself: X BUT H.
· Anti-reflexivity.
A is anti-reflexive if A  E =
E = 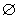 i.e. it is executed only for non-coinciding objects: from Xi А Xj it follows that Xi ¹ Xj (strict inequality; "be older").
i.e. it is executed only for non-coinciding objects: from Xi А Xj it follows that Xi ¹ Xj (strict inequality; "be older").
· Symmetry.
The ratio A is symmetrical if A = A-1 , i.e., if the ratio Xi is satisfied And Xj is the ratio Xj A xi ("Be a brother").
· Asymmetry.
The ratio A is asymmetrical if A  A-1 = Æ, i.e., of the two relations Xi A Xj and Xj A Xi, one is wrong (“being a father”). If the relation A is asymmetric, then it is also antireflexive.
A-1 = Æ, i.e., of the two relations Xi A Xj and Xj A Xi, one is wrong (“being a father”). If the relation A is asymmetric, then it is also antireflexive.
· Antisymmetry.
The ratio A is antisymmetric if A  A-1 Ì E , that is, both relations Xi А Xj and Xj А Xi are fulfilled simultaneously only when Xi = Xj .
A-1 Ì E , that is, both relations Xi А Xj and Xj А Xi are fulfilled simultaneously only when Xi = Xj .
· Transitivity.
The relation A is transitive if the relation Xi А Xj and Xj А Xk implies the relation Xi А Xk (“to be a divisor”).
For a Reflexive Relationship, all elements of the matrix on the main diagonal are 1; for an Anti-Reflexive Relationship, these are zeros.
The symmetry of the relationship entails the symmetry of the matrix; Asymmetry Relationships - asymmetry of the matrix with zero elements on the main diagonal; Antisymmetry - only asymmetry of the matrix.
In the matrix of the Transitive relation for each pair of unit elements, one of which is located in the I- th column and J- th row, and the other - in the J- th column and K - th row, there is necessarily a single element located in the I- th column and K - th line. The presence of single elements on the main diagonal does not violate transitivity.
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.