Equivalence relation

Lecture

The equivalence relation is a rigorous mathematical definition of such ordinary notions as “sameness” or “indistinguishability”.

Denoted by X ~ Y. The equivalence relation A in the set M means that the ordered pair ( X , Y ) belongs to the set A Ì M ´ M.

The equivalence relation has the properties:

· Reflexivity : X ~ Y ;

· Symmetry : if X ~ Y , then Y ~ X ;

· Transitivity : if X ~ Y and Y ~ Z , then X ~ Z.

The most important value of equivalence is that this relation defines a feature that allows splitting of the set M into disjoint subsets, called Klas Sami equivalences. And vice versa: every partition of the set M into non-intersecting subsets defines some equivalence relation between the elements of this set.

For example : The “live in one house” relationship, defined in a multitude of city dwellers, is an equivalence and breaks this multitude into disjoint subsets of people who are neighbors in the house.

All elements belonging to a certain class M I of the partition { M1, M2, ..., M N } of the set M into equivalence classes are related by an equivalence relation. Any of these elements defines this class and can serve as its Representative or Benchmark .

An arbitrary equivalence relation defines a generalized form of equality on some set. Equivalence classes consist of all those elements that are indistinguishable from the point of view of a given equivalence relation. Moreover, each class is determined by its representative (standard) and is identified with some common property or set of properties of its constituent elements.

The limiting case of an equivalence relation is Identical equality . Obviously, the only element that is identically equal to any given element is that element itself. Therefore, in this case, we have the most complete partition, in which the equivalence classes contain only one element of the original set.

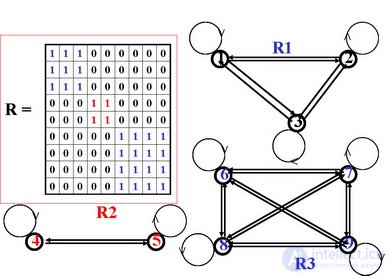
Consider the equivalence relation matrix.

Elements belonging to a certain equivalence class are pairwise equivalent to each other, and their sections coincide. Consequently, the columns of the equivalence relation matrix for elements of the same class are the same and contain “1” in all rows that correspond to these elements. Since equivalence classes do not overlap, there will be no units in the same rows in columns of different classes. If we arrange the elements of a set so that in each equivalence class the elements belonging to it are next to each other, then the unit elements of the matrix form disjoint squares, the diagonals of which are located on the main diagonal of the matrix.

For example : Let the set M be divided into equivalence classes as follows:

M1 = { X1, x2, x3 }; M2 = { X4 }; M3 = { X5, x6, x7, x8 }.

The signs according to which the elements of a set are divided into classes may be the most diverse, but still such a sign is not completely arbitrary.

Xi Xj	X 1	X 2	X3	X 4	X5	X 6	X7	X 8
X 1	one	one	one
X 2	one	one	one
X3	one	one	one
X 4				one
X5					one	one	one	one
X 6					one	one	one	one
X7					one	one	one	one
X 8					one	one	one	one

Suppose, for example , that we want to divide the points of the plane into classes, assigning two points to the same class in that, and only if the distance between them is less than 1. Let the distance from point A to point B be less than 1, and the distance from B C is also less than 1. Then, by placing A in one class with B , and B in one class with C , we must classify C in one class with A. But the distance from A to C can be more than 1. Therefore, such a sign does not allow splitting the set into equivalence classes. This is explained by the fact that for it the property of transitivity does not hold: if A ~ B , and B ~ C , then A ~ C. Thus, it is possible to define the equivalence relation as a binary relation for which the properties of reflexivity, symmetry and transitivity are satisfied.

Fulfillment of these conditions is necessary and sufficient for the given attribute to allow partitioning the set into equivalence classes.

Example: on a set of 6 below graphs

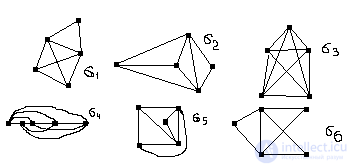
we construct a graph corresponding to the equivalence relation.

Decision:

because the equivalence relation on the set of objects is a combination of three properties - reflexivity, symmetry and transitivity, then we have:

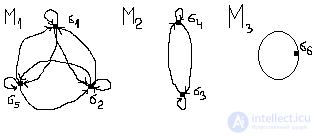
Here: M ₁ M = {σ ₁ , σ ₂ , σ ₃ , σ ₄ , σ ₅ , σ ₆ }, M _i is the set of pairwise isolated graphs, i.e. M ₁ = {σ ₁ , σ ₂ , σ ₅ }. Similarly, M ₂ M and M ₂ = {σ ₃ , σ ₄ }, M ₃ M and M ₃ = {σ ₆ }. Thus, by an equivalence relation, the set M of 6 graphs is divided into three disjoint subsets of isomorphic graphs M ₁ M ₂ = Ø, M ₁ M ₃ = Ø, M ₂ M ₃ = M, M ₁ M ₂ M ₃ = M.