Lecture
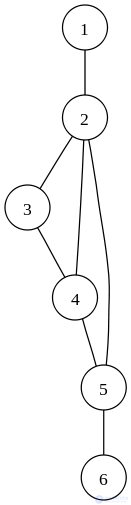
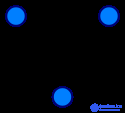
A graph is the main object of study of mathematical graph theory, a collection of a nonempty set of vertices and sets of pairs of vertices (connections between vertices).
Objects are represented as vertices or nodes of a graph, and links as arcs, or edges [1] . For different applications, types of graphs can vary in direction, restrictions on the number of links, and additional data on vertices or edges.
Many structures of practical interest in mathematics and computer science can be represented by graphs. For example, the structure of Wikipedia can be modeled using a directed graph (digraph), in which vertices are articles, and arcs (oriented edges) are hyperlinks (thematic map).
Graph theory does not have established terminology. In different articles, the same terms mean different things. Below are the most common definitions.
Graph or undirected graph 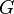 - this is an ordered pair.
- this is an ordered pair. 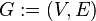 where
where 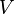 Is a non-empty set of vertices or nodes , and
Is a non-empty set of vertices or nodes , and 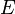 - the set of pairs (in the case of an undirected graph - unordered) vertices, called edges .
- the set of pairs (in the case of an undirected graph - unordered) vertices, called edges .
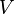 (and therefore,
(and therefore, 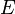 otherwise it would be a multiset) are usually considered finite sets. Many results obtained for finite graphs are incorrect (or differ in some way) for infinite graphs , since not all the assertions that hold for finite sets are fulfilled in the case of infinite sets.
otherwise it would be a multiset) are usually considered finite sets. Many results obtained for finite graphs are incorrect (or differ in some way) for infinite graphs , since not all the assertions that hold for finite sets are fulfilled in the case of infinite sets.
The vertices and edges of the graph are also called the elements of the graph, the number of vertices in the graph 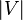 - order , the number of edges
- order , the number of edges 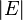 - the size of the graph.
- the size of the graph.
Vertices 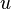 and
and 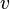 are called end vertices (or just ends ) edges
are called end vertices (or just ends ) edges 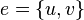 . The edge, in turn, connects these vertices. Two end vertices of the same edge are called adjacent .
. The edge, in turn, connects these vertices. Two end vertices of the same edge are called adjacent .
Two edges are called adjacent if they have a common terminal vertex.
Two edges are called multiple if the sets of their terminal vertices coincide.
An edge is called a loop if its ends coincide, that is, 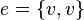 .
.
Degree 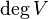 tops
tops 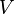 call the number of edges incident to it (with the loop counting twice).
call the number of edges incident to it (with the loop counting twice).
A vertex is called isolated if it is not an end for any edge; hanging (or sheet ), if it is the end of exactly one edge.
Oriented graph (abbreviated digraph ) 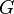 - this is an ordered pair.
- this is an ordered pair. 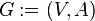 where
where 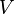 - a non-empty set of vertices or nodes , and
- a non-empty set of vertices or nodes , and 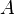 - A set of (ordered) pairs of different edges, called arcs or oriented edges .
- A set of (ordered) pairs of different edges, called arcs or oriented edges .
An arc is an ordered pair of vertices. 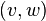 where is the top
where is the top 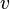 called the beginning as well
called the beginning as well 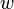 - the end of the arc. We can say that the arc
- the end of the arc. We can say that the arc 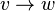 leads from the top
leads from the top 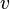 to the top
to the top 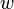 .
.
Mixed graph 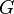 - is a graph in which some edges may be oriented, and some - non-oriented. It is recorded in an orderly three.
- is a graph in which some edges may be oriented, and some - non-oriented. It is recorded in an orderly three. 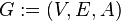 where
where 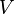 ,
, 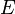 and
and 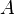 defined as above.
defined as above.
Oriented and undirected graphs are special cases of mixed.
Graph 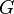 called isomorphic to a graph
called isomorphic to a graph 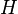 if there is a bijection
if there is a bijection 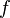 from the set of vertices of the graph
from the set of vertices of the graph 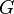 in many vertices of the graph
in many vertices of the graph 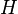 with the following property: if in the column
with the following property: if in the column 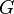 there is an edge from the top
there is an edge from the top 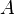 to the top
to the top 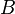 then in the graph
then in the graph 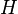 there must be an edge from the top
there must be an edge from the top 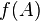 to the top
to the top 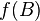 and vice versa - if in the graph
and vice versa - if in the graph 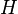 there is an edge from the top
there is an edge from the top 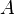 to the top
to the top 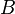 then in the graph
then in the graph 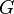 there must be an edge from the top
there must be an edge from the top 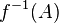 to the top
to the top 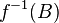 . In the case of a directed graph, this bijection must also preserve the orientation of the edge. In the case of a weighted graph, the bijection must also preserve the weight of the edge.
. In the case of a directed graph, this bijection must also preserve the orientation of the edge. In the case of a weighted graph, the bijection must also preserve the weight of the edge.
A route in a graph is a finite sequence of vertices in which each vertex (except the last) is connected to the next edge in the sequence. A chain is a route without repeated edges. A simple chain is a route without repeating vertices (whence it follows that there are no repeating edges in a simple chain).
Oriented route (or path ) in a digraph is a finite sequence of vertices and arcs in which each element is incident to the previous and next.
A cycle is a chain in which the first and last vertices coincide. The length of the path (or cycle) is called the number of its edges . Note that if the vertices 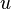 and
and 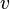 are the ends of some edge, then according to this definition, the sequence
are the ends of some edge, then according to this definition, the sequence 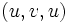 is a cycle. To avoid such “degenerate” cases, the following concepts are introduced.
is a cycle. To avoid such “degenerate” cases, the following concepts are introduced.
The path (or cycle) is called simple if the edges in it do not repeat; elementary if it is simple and the vertices are not repeated in it. It is not difficult to see that:
A binary relation on the set of vertices of the graph, given as "there is a path from 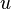 at
at 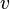 , Is an equivalence relation and, therefore, splits this set into equivalence classes, called the connected components of the graph. If the graph has exactly one connected component, then the graph is connected. On the connected component, one can introduce the concept of the distance between vertices as the minimum length of the path connecting these vertices.
, Is an equivalence relation and, therefore, splits this set into equivalence classes, called the connected components of the graph. If the graph has exactly one connected component, then the graph is connected. On the connected component, one can introduce the concept of the distance between vertices as the minimum length of the path connecting these vertices.
Every maximal connected subgraph of a graph G is called a connected component (or simply a component) of a graph 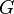 . The word "maximum" means maximum relative to inclusion, that is, not contained in a connected subgraph with a large number of elements.
. The word "maximum" means maximum relative to inclusion, that is, not contained in a connected subgraph with a large number of elements.
An edge of a graph is called a bridge if its removal increases the number of components.
Count is called:
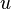 ,
, 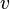 there is a way out
there is a way out 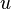 at
at 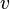 .
. 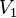 and
and 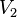 so that every edge connects a vertex from
so that every edge connects a vertex from 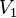 with top of
with top of 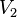 .
. 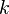 disjoint subsets
disjoint subsets 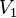 ,
, 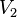 , ...,
, ..., 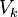 so that there will be no edges connecting the vertices of the same subset.
so that there will be no edges connecting the vertices of the same subset. It also happens:
A simple graph is a one-dimensional simplicial complex.
More abstract, the graph can be set as a triple 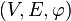 where
where 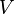 and
and 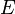 - some sets ( vertices and edges , respectively), and
- some sets ( vertices and edges , respectively), and 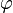 - the incidence function (or incidentor ) associating each edge
- the incidence function (or incidentor ) associating each edge 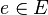 (ordered or unordered) a pair of vertices
(ordered or unordered) a pair of vertices 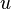 and
and 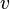 of
of 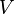 (his ends ). Special cases of this concept are:
(his ends ). Special cases of this concept are:
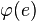 always an ordered pair of vertices;
always an ordered pair of vertices; 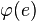 always an unordered pair of vertices;
always an unordered pair of vertices; Under this definition some other generalizations do not fit:
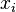 and
and 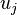 There are binary relations of incidence.
There are binary relations of incidence. A table where both columns and rows correspond to the vertices of the graph. In each cell of this matrix, a number is written that determines whether there is a connection from the vertex-row to the vertex-column (or vice versa).
The disadvantage is the memory requirements that are directly proportional to the square of the number of vertices.
Each row corresponds to a certain vertex of the graph, and the columns correspond to the connections of the graph. In the cell at the intersection 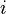 -th line with
-th line with 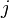 -m column of the matrix is written:
-m column of the matrix is written:
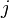 "Coming out" from the top
"Coming out" from the top 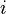 ,
, This method is the most capacious (the size is proportional to 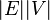 ) for storage, but makes it easier to find cycles in the graph.
) for storage, but makes it easier to find cycles in the graph.
The edge list is a type of graph representation, implying that each edge is represented by two numbers - the numbers of the vertices of this edge.
For the description of graphs for purposes suitable for machine processing and at the same time convenient for human perception, several standardized languages are used, including:
A series of commercial programs for graph construction has been developed, for example, graph construction underlies the ILOG application software packages (owned by IBM since 2009), among others are GoView, Lassalle AddFlow, LEDA (there is a free edition).
There is also a free program for constructing graphs igraph and a free library Boost (free software).
To visualize graphs you can use:
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.