Lecture
The order relation is usually denoted by £. The notation X £ Y means that the pair ( X, y ) belongs to the set A Ì M ´ M , which is an order relation in M , and X precedes Y (or Y follows X ).
The order relation has the properties:
· Reflexivity x £ X ;
· Transitivity; If X £ Y , and Y £ Z , then X £ Z ;
· Antisymmetry; If X £ Y , and Y £ X , then X = Y.
The set on which the order relation is defined is called Ordered , and it is said that the order is introduced by this relation.
If for any two elements X and Y of the set M, the relation X £ Y (or Y £ X ), then M - Completely (linearly) orderly .
For example , a set of natural or real numbers with a natural ratio of order £ are perfectly ordered.
In the general case, it may turn out that for some pairs ( X, y ) none of the ratios X £ Y and Y £ X does not hold. Such elements are called Incomparable , and the set M is called Partially ordered .
Examples of partial order are the relation “to be a divisor”, the inclusion relation Ì, etc. Thus, the inclusion relation on the set of subsets M I of a certain universe M is reflexive ( M I Ì M I ), transitive (if M I Ì M J , a M J Ì M K , then M I Ì M K ) and antisymmetrically (from M I Ì M J , and M J Ì M I follows M I = M J ), but among all possible subsets there are such that none of the ratios of M I Ì M N , and M N Ì M I It does not take place. Similarly, not all pairs of elements from the set of natural numbers are in the relation “to be a divisor”.
This note discusses one of the most commonly used binary relations, the relationship of order.
Order plays a huge role in our lives. People throughout history have tried to streamline relations among themselves, the surrounding phenomena. Without order it is impossible to imagine human life. Try to imagine a society in which anarchy reigns or a dictionary in which words are arranged chaotically. But what is order? With some orderings, we are so accustomed that often they are simply not aware of, such as the grammatical order of words in a sentence. This article provides a formal definition of the order used in mathematics.
Definition 1.1 . A binary relation a on a set X is called an order relation if it is transitive :
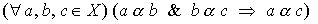
and antisymmetrically :
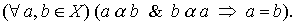
Example 1.1 . Consider the attitude of "older" on many people. Obviously, it is transitive and antisymmetric, and, therefore, is an order relation.
Example 1.2 . The hierarchy of animals, built on the stages of evolution, is a relation of order (Fig. 1).
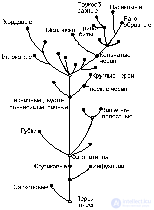
Fig. 1. The main stages of the evolution of eukaryotic organisms
Definition 1.2 . The set X with the order relation defined on it 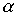 is called an ordered set and is denoted by
is called an ordered set and is denoted by 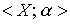 .
.
Ordered set 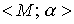 with a small number of elements is visually represented as a directed graph. In this case, the elements of the set M are associated with the vertices of the graph (indicated by dots in the figure), and the elements of the relation a with arcs (lines with arrows).
with a small number of elements is visually represented as a directed graph. In this case, the elements of the set M are associated with the vertices of the graph (indicated by dots in the figure), and the elements of the relation a with arcs (lines with arrows).
For example, Figure 2 shows a directed graph representing the relation 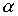 = {( a , a ), ( a , b ), ( a , c ), ( b , c)} on the set M = { a , b , c , d }.
= {( a , a ), ( a , b ), ( a , c ), ( b , c)} on the set M = { a , b , c , d }.
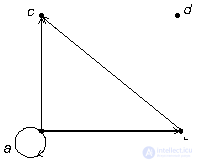
Fig. 2. Graph of an ordered set
You can set the order on the set in various ways. So, for example, in Figure 3 three ways of streamlining the four countries are shown.
| Square | Russia | USA | France | England |
| Population | USA | Russia | France | England |
| Population density | England | France | USA | Russia |
Fig. 3. Three ways to streamline
Figure 4 shows oriented graphs representing the relations "divided" and "less" on the set M = { 1 , 2 , 3 , 4 } of natural numbers.
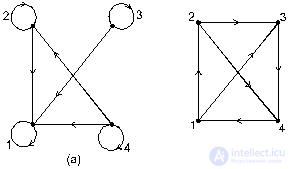
Fig. 4. Graphs of relations "divided" (a) and "less" (b) on the set { 1 , 2 , 3 , 4 }
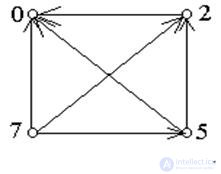
Example. M = {0; 2; 5; 7}. M2 = {<0; 0>; <0; 2>; <0; 5>; <0; 7>; <2; 0>; <2; 2>; <2; 5>; <2; 7> ; <5; 0>; <5; 2>; <5; 5>;
<5; 7>; <7; 0>; <7; 2>; <7; 5>; <7; 7>}.
From the set M2, we select a subset R of those pairs in which a> b. R = {<2; 0>; <5; 0>; <5; 2>; <7; 0>; <7; 2>; <7; 5>;}. The set R defines the “more” relation for the elements of the set M. The graph corresponding to this relation is shown in Fig. 5. Each arrow is directed from a larger number to a smaller one.
 |
 |
Definition 2.1 . A relation of order a is called a relation of non - strict order on a set X , if a is reflexive :
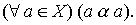
The ratio of non-strict order is usually denoted by the symbol 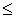 . If a
. If a 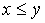 , then they say that "the element x precedes the element y " or " y follows x ".
, then they say that "the element x precedes the element y " or " y follows x ".
Example 2.1 . Attitude 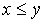 on the set of real numbers is a nonstrict order relation.
on the set of real numbers is a nonstrict order relation.
Example 2.2 . On the set of subsets of some universal set U, the relation 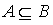 is a nonstrict order relation.
is a nonstrict order relation.
Example 2.3 . The relationship of subordination in the institution is not strict order on a set of employees of the institution.
Example 2.4 . Attitude 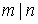 ( m divides n ) on an arbitrary subset of natural numbers is a non-strict order. Figure 5 shows the graph corresponding to the ordered set
( m divides n ) on an arbitrary subset of natural numbers is a non-strict order. Figure 5 shows the graph corresponding to the ordered set 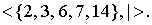
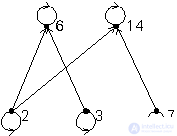
Fig. 5. Graph of a non-strictly ordered set
Example 2.5 . The identity relation is both an equivalence relation and a non-strict order relation.
Definition 2.2 . Two elements 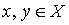 are called comparable elements of an ordered set X if either
are called comparable elements of an ordered set X if either 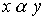 either
either 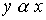 .
.
The incomparable elements in the ordered set of example 4 are, for example, elements 7 and 2, 2 and 3, 3 and 7.
Definition 2.3 . An order relation a is called a strict order relation on a set X if a is anti-reflexive :
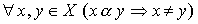 .
.
A strict order relation is denoted by <.
Example 2.6 . Let f and g be functions with the same domains. We define the relation> as follows: f > g , if for any x from the domain of the function f ( x )> g ( x ). Obviously, this relation is a strict order relation.
For the functions f and g shown in Fig. 6, the relation f > g holds. The pairs of functions f and h , as well as g and h, are incomparable.

Fig. 6. Three functions
Example 2.7 . The alphabetic order is a strict order relation on a set of letters.
Example 2.8 . Let a strictly order relation be given on the set X 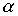 . How can you set a strict order relation on a set
. How can you set a strict order relation on a set 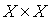 , that is, how to compare pairs of elements from the set X ? One of the possible options is as follows. On the set X, we define a relation
, that is, how to compare pairs of elements from the set X ? One of the possible options is as follows. On the set X, we define a relation 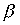 condition:
condition:
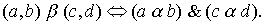
Attitude 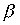 is a strict order.
is a strict order.
Example 2.9. Another way to set a strict order on a set 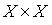 is as follows. We assume that the relation ( a , b ) holds
is as follows. We assume that the relation ( a , b ) holds 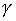 ( c , d ) if
( c , d ) if
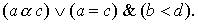
This order relation is called lexicographic . In general, it is defined as follows. For the words v and w of the same length, we assume that v < w , if there exists a number k such that 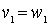 ,
, 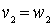 , ...,
, ..., 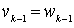 ,
, 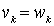 where
where  - i - th letters of the words v and w, respectively. For words
- i - th letters of the words v and w, respectively. For words 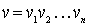 and
and 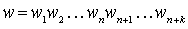 ( k > 0 ) of different length is considered v < w , if
( k > 0 ) of different length is considered v < w , if 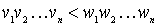 or
or 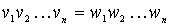 and w < v , if
and w < v , if 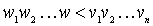 . This sorting method is used in dictionaries. In this order, for example:
. This sorting method is used in dictionaries. In this order, for example:
childhood
Institute
12 <123 <4.
As already noted, it is convenient to represent ordered sets as graphs. Moreover, if 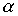 is a strictly order relation, then the relation graph a does not contain cycles. The converse is also true: for any graph G without cycles, there exists a relation a of strict order such that the graph associated with this relation coincides with the transitive closure of the graph G. (The transitive closure of a graph G is a graph obtained from a graph G by adding arcs connecting each vertex a with vertices reachable from a .) Indeed, let G be a graph without contours. We define the relation on the set M of vertices of this graph
is a strictly order relation, then the relation graph a does not contain cycles. The converse is also true: for any graph G without cycles, there exists a relation a of strict order such that the graph associated with this relation coincides with the transitive closure of the graph G. (The transitive closure of a graph G is a graph obtained from a graph G by adding arcs connecting each vertex a with vertices reachable from a .) Indeed, let G be a graph without contours. We define the relation on the set M of vertices of this graph 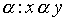 if there is a path in the direction of the arcs leading from x to y . It is easy to see that due to the absence of cycles, the relation
if there is a path in the direction of the arcs leading from x to y . It is easy to see that due to the absence of cycles, the relation 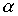 is a strict order.
is a strict order.
Definition 2.4 . X set with binary relation 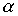 called connected if for any two different elements x and y from X either
called connected if for any two different elements x and y from X either 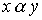 either
either 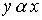 .
.
Definition 2.5 . A connected order relation on a set X is called a linear order relation.
Example 2.10 . The lexicographical order of words in a dictionary is a linear order.
Example 2.11 . The inclusion relation on a set of figures is not a linear order (Fig. 7).
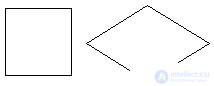
Fig. 7. Two incomparable figures
Example 2.12 . The attitude of "older" on many people is a linear order.
Example 2.13 . Consider a lot of people. They can be ordered in different ways, for example, by height (Fig. 8).

Fig. 8. The rank
The ordering of the elements of the set X by mapping its elements into some ordered set Y is a fairly typical example of order determination.
The corresponding general method of ordering a set is as follows. Let an injective function be defined on a set X
f : X ® R ,
accepting real numeric values. Set the relation X by the condition: x < y if f ( x ) < f ( y ). Thus, a certain relation is f ( x ) < f ( x ) cannot be. The transitivity and antisymmetry of the relationship Finally, for any pair of different elements x , y from X, either f ( x ) < f ( y ) or f ( y ) < f ( x ) is true, since f is an injection. So the order The function f one-to-one maps our set X onto some subset of the set R of real numbers, so the relation x < y for any elements of the set X is equivalent to the inequality f ( x ) < f ( y ).
Definition 2.6 . Let a strict order relation X be given. The element x X X such that for every y from X that does not coincide with x , the relation x < y ( x > y ) holds is called the smallest ( largest ).
Definition 2.7 . Let a relation of strictly order X. Then the element 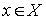 is called minimal ( maximal ) in the ordered set < X , <> if there is no element y for which y < x (respectively, y > x ).
is called minimal ( maximal ) in the ordered set < X , <> if there is no element y for which y < x (respectively, y > x ).
If, as usual, in the case of x < y, to draw an arrow from x to y , then in the relation graph the minimum element is the one into which the arrows do not enter, and the maximum element from which the arrows do not extend.
In the case of a linear strictly order, the minimal element x has the additional property that for every 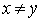 done x < y . Thus, for the case of linear orders, the concept of the minimal element coincides with the concept of the smallest element. In the general case, it may turn out that the element x is minimal, but is not in the relation x < y with any other elements. For example, in Figure 5, element 2 is minimal, but not comparable with elements 3 and 7.
done x < y . Thus, for the case of linear orders, the concept of the minimal element coincides with the concept of the smallest element. In the general case, it may turn out that the element x is minimal, but is not in the relation x < y with any other elements. For example, in Figure 5, element 2 is minimal, but not comparable with elements 3 and 7.
To understand the difference between minimal and minimal elements, consider an example.
Example 2.14. Figure 9 shows a diagram of an ordered set, in which there are neither the smallest nor the largest elements, but at the same time there is exactly 1 minimal and exactly 1 maximal elements.
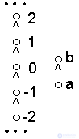
Fig.9. Ordered set
Consider the finite strictly ordered sets in more detail.
Lemma 2.1. If a linear strict order is given on a finite (non-empty) set X , then there exists a smallest element, and it is unique.
Evidence. Take an arbitrary element 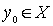 . If a
. If a 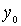 - the smallest element, then the existence of the desired element is proved. If not, then since
- the smallest element, then the existence of the desired element is proved. If not, then since 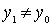 , what
, what 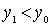 . Again either
. Again either 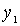 - the smallest, or exists
- the smallest, or exists 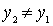 such that
such that 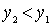 . We will continue this process. Suppose that n + 1 elements are already selected for which
. We will continue this process. Suppose that n + 1 elements are already selected for which
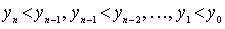 .
.
By transitivity, it is clear that  with i > j . Hence, due to anti-reflexivity, all the selected elements are not equal in pairs. Therefore, in view of the finiteness of the set X, the selection process must be interrupted in a finite number of steps. Element
with i > j . Hence, due to anti-reflexivity, all the selected elements are not equal in pairs. Therefore, in view of the finiteness of the set X, the selection process must be interrupted in a finite number of steps. Element 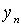 , chosen in the last step, will obviously be the desired one. So for any
, chosen in the last step, will obviously be the desired one. So for any 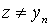 done
done 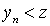 . We show that this element is unique. Indeed, let there be another element
. We show that this element is unique. Indeed, let there be another element 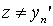 such that, for everyone
such that, for everyone 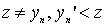 . Then simultaneously executed
. Then simultaneously executed 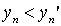 and
and 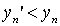 that is impossible due to antisymmetry. The lemma is proved.
that is impossible due to antisymmetry. The lemma is proved.
Theorem 2.1. Let a relation of linear strict order X. Then on X you can choose this numbering. 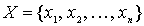 what's the ratio
what's the ratio  will be performed if and only if i < j .
will be performed if and only if i < j .
Evidence. Let be 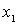 - the smallest element in the set X , chosen according to Lemma 1. Denote by
- the smallest element in the set X , chosen according to Lemma 1. Denote by 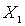 lots of
lots of 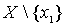 . Denote by
. Denote by 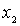 smallest element of the set
smallest element of the set 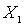 . It's clear that
. It's clear that 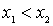 . Remove from
. Remove from 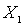 element
element 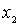 and the remaining set is denoted by
and the remaining set is denoted by 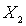 . Its smallest element
. Its smallest element 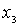 satisfies the condition:
satisfies the condition: 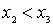 . The numbering procedure is already clear: going through all the elements of X sequentially using the indicated method, we will line them up:
. The numbering procedure is already clear: going through all the elements of X sequentially using the indicated method, we will line them up:
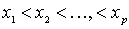 ,
,
where p is the number of elements in X. By virtue of transitivity and antisymmetry, it is clear that 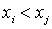 if and only if i < j . The theorem is proved.
if and only if i < j . The theorem is proved.
In essence, this theorem means that any linear strict order on a finite set X is equivalent to the usual order on some segment of the natural series.
The relation of order is directly related to the relation of dominance.
Definition 2.8. Let be 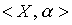 is an ordered set, x and y are its elements. We say that x dominates y , if
is an ordered set, x and y are its elements. We say that x dominates y , if 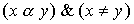 but there is no such element z О X that
but there is no such element z О X that 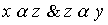 .
.
With the help of the dominance relation, you can introduce another visual way of representing ordered sets - Hasse diagrams . In the diagrams, each element is represented by a point in the plane, and if y dominates x , then x and y are joined by a segment, with the point corresponding to x located below y .
Consider three partial order relations and construct Hasse diagrams for them.
Example 2.15. Let A = { 1 , 2 , 3 }. On the set of all subsets of the set A, consider the relationship "to be a subset". A diagram of this ordered set is shown in Figure 10 (a).
Example 2.16. Let X = { 1 , 2 , 3 , 5 , 6 , 10 , 15 , 30 }. We introduce the relation "divided" on this set. The diagram of this ordered set is shown in Figure 10 (b).
Example 2.17. On the set X = { 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 }, consider the relation of linear order <. His diagram is shown in Figure 10 (c).
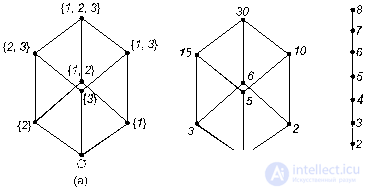
Fig. 10. Hasse diagrams
Note that the Hasse diagrams of the first two relations are the same. This means that these partially ordered sets have the same structure, and this is different from the structure of the third ordered set, although it also contains eight elements. More precisely, such a common structure is defined by the concept of isomorphism.
Definition 2.9. Two ordered sets 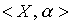 and
and 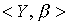 are called isomorphic if there is a bijection
are called isomorphic if there is a bijection 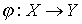 preserving the relation of order. In other words,
preserving the relation of order. In other words, 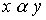 then and only if
then and only if 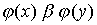 where
where 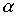 and
and 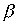 - отношения порядка, заданные на множествах X и Y соответственно.
- отношения порядка, заданные на множествах X и Y соответственно.
Упорядоченные множества, рассмотренные в примерах 1 и 2 изоморфны.
Теорема 2.2. Всякое нестрого упорядоченное множество 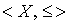 изоморфно некоторой системе подмножеств множества X , нестрого упорядоченной отношением включения.
изоморфно некоторой системе подмножеств множества X , нестрого упорядоченной отношением включения.
Доказательство. Для каждого элемента 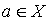 рассмотрим множество
рассмотрим множество 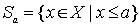 . Then
. Then 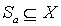 and
and 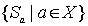 - совокупность всех таких подмножеств. Докажем, что эта система подмножеств, нестрого упорядоченная отношением включения, изоморфна
- совокупность всех таких подмножеств. Докажем, что эта система подмножеств, нестрого упорядоченная отношением включения, изоморфна 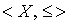 . Рассмотрим отображение
. Рассмотрим отображение 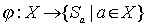 такое, что
такое, что 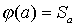 . Then
. Then 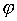 - биекция. Действительно, если
- биекция. Действительно, если 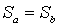 , то, поскольку
, то, поскольку 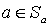 , в силу рефлексивности
, в силу рефлексивности 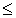 , имеем
, имеем 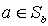 and
and 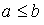 . Аналогично получаем
. Аналогично получаем 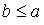 и в силу антисимметричности
и в силу антисимметричности 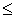 имеем a = b , т. е. отображение
имеем a = b , т. е. отображение  инъективно. Besides,
инъективно. Besides,  сюръективно, так как у любого подмножества
сюръективно, так как у любого подмножества 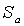 есть прообраз a . Докажем теперь, что отображение сохраняет отношение частичного порядка. Пусть
есть прообраз a . Докажем теперь, что отображение сохраняет отношение частичного порядка. Пусть 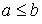 . Тогда для любого
. Тогда для любого 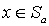 из
из 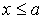 в силу транзитивности отношения
в силу транзитивности отношения 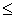 следует
следует 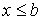 , а значит, и
, а значит, и 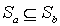 . Если
. Если 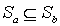 , то, поскольку
, то, поскольку 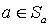 , имеем
, имеем 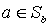 , поетому
, поетому 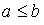 .
.
Перейдем теперь к обсуждению вопросов, связанных с упорядочением по разным критериям. Пусть у нас имеется несколько отношений порядка. Как по ним построить новое отношение порядка?
Исходя из операций над множествами, мы можем определить ряд операций над отношениями. Далее будем полагать, что все отношения заданы на одном и том же множестве X .
Возьмем два отношения 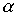 and
and 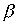 . Каждому из них соответствует некоторое множество пар (подмножества
. Каждому из них соответствует некоторое множество пар (подмножества 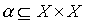 and
and 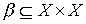 ).
).
Определение 3.1. Пересечением отношений 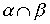 называется отношение, определяемое пересечением соответствующих подмножеств. Ясно, что
называется отношение, определяемое пересечением соответствующих подмножеств. Ясно, что 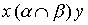 выполнено тогда и только тогда, когда одновременно выполнены соотношения
выполнено тогда и только тогда, когда одновременно выполнены соотношения 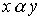 и.
и.
Пример 3.1. Пусть X - множество вещественных чисел, a - отношение "быть не меньше", b - отношение "быть строго больше". Then 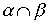 есть отношение "быть строго больше".
есть отношение "быть строго больше".
Определение 3.2. Объединением отношений 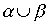 называется отношение, определяемое объединением соответствующих множеств. Соотношение
называется отношение, определяемое объединением соответствующих множеств. Соотношение 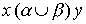 выполнено тогда и только тогда, когда выполнено хотя бы одно их соотношений
выполнено тогда и только тогда, когда выполнено хотя бы одно их соотношений 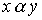 or
or 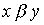 .
.
Пример 3.2. Если 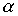 - отношение "больше" на множестве чисел, а
- отношение "больше" на множестве чисел, а 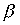 - отношение "равно", то
- отношение "равно", то 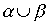 - это отношение
- это отношение 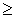 .
.
Можно ввести операции непосредственно не сводящиеся к теоретико-множественным.
Определение 3.3. Обратным отношением называется отношение, определяемое условием: 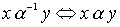 .
.
Пример 3.3. Пусть 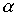 - отношение "делит", тогда
- отношение "делит", тогда 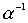 - отношение "делится".
- отношение "делится".
Определение 3.4. Произведением отношений называется отношение, определяемое следующим образом: соотношение 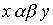 равносильно тому, что существует такой элемент
равносильно тому, что существует такой элемент 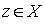 , для которого выполнены соотношения
, для которого выполнены соотношения 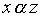 and
and 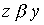 .
.
Пример 3.4. Пусть 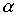 - отношение "быть женой", а
- отношение "быть женой", а 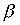 - отношение "быть отцом". Что означает в этом случае соотношение
- отношение "быть отцом". Что означает в этом случае соотношение 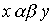 ? По определению существует такой z , что " x - жена z " и " z - отец y ". Другими словами, " x есть жена отца y ", т.е. " x - мать или мачеха y ".
? По определению существует такой z , что " x - жена z " и " z - отец y ". Другими словами, " x есть жена отца y ", т.е. " x - мать или мачеха y ".
Пример 3.5. Пусть 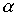 - отношение "быть братом", а
- отношение "быть братом", а  - отношение "быть родителем". Тогда произведение
- отношение "быть родителем". Тогда произведение 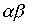 есть отношение "быть братом одного из родителей", т.е. "быть дядей".
есть отношение "быть братом одного из родителей", т.е. "быть дядей".
Прежде чем мы перейдем к теоремам, относящимся к отношению порядка, рассмотрим несколько вспомогательных утверждений (ввиду их простоты мы приводим их без доказательства).
Лемма 3.1. Если отношения 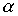 and
and 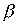 рефлексивны, то рефлексивны и следующие отношения:
рефлексивны, то рефлексивны и следующие отношения:
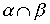 ,
, 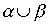 ,
, 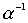 ,
, 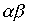 .
.
Лемма 3.2. Если отношения 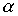 and
and 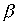 симметричны, то симметричны и следующие отношения:
симметричны, то симметричны и следующие отношения:
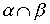 ,
, 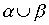 ,
, 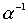 .
.
Лемма 3.3. Чтобы произведение 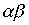 симметричных отношений
симметричных отношений 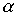 and
and 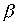 было симметрично, необходимо и достаточно, чтобы отношения
было симметрично, необходимо и достаточно, чтобы отношения 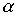 and
and 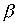 коммутировали.
коммутировали.
Лемма 3.4. Если отношения a и b - антисимметричны, то антисимметричны также и следующие отношения: 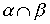 ,
, 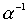 .
.
Антисимметричность может не сохраняться при объединении и произведении.
Лемма 3.4. Если отношения 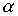 and
and 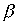 транзитивны, то транзитивны также следующие отношения:
транзитивны, то транзитивны также следующие отношения: 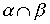 ,
, 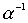 .
.
Из лемм 3.1, 3.2, 3.3, 3.4 вытекают следующие две теоремы.
Теорема 3.1. Если 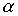 and
and 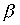 - строгие порядки (нестрогие порядки), то пересечение
- строгие порядки (нестрогие порядки), то пересечение 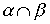 также является строгим порядком (нестрогим порядком).
также является строгим порядком (нестрогим порядком).
Замечание. Пересечение строгого и нестрогого порядка есть строгий порядок.
The property "to be a linear order" is not required to be maintained at the intersection. This is easiest to see from the following considerations. Let a be a linear order (strict or non-strict), then 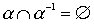 (or = E ). Therefore,
(or = E ). Therefore, 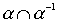 on a set of more than one element it is not a linear order.
on a set of more than one element it is not a linear order.
Theorem 3.2. If the relation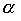 is a strict (nonstrict, linear) order, then the relation
is a strict (nonstrict, linear) order, then the relation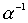 is a strict (nonstrict, linear) order.
is a strict (nonstrict, linear) order.
Combining orders in the general case is not an order. This is clearly seen in this example. Let be 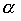 a linear weak order, then
a linear weak order, then 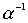 there is a relation of the same type. However, association
there is a relation of the same type. However, association 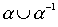 is a complete relationship, and, therefore, is not an order. The following are without proof of the conditions under which the union of orders is an order.
is a complete relationship, and, therefore, is not an order. The following are without proof of the conditions under which the union of orders is an order.
Theorem 3.3. If a and
and 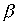 - strict orders, the union
- strict orders, the union 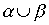 is a strict order if and only if
is a strict order if and only if
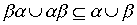 .
.
Theorem 3.4. In order to combine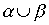 weak orders
weak orders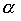 and
and 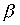 was lax order, it is necessary and sufficient to meet the conditions
was lax order, it is necessary and sufficient to meet the conditions
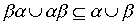 ,
,
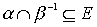 .
.
Произведение порядков 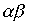 также не обязано быть порядком. Это видно из того хотя бы, что для линейного нестрогого порядка
также не обязано быть порядком. Это видно из того хотя бы, что для линейного нестрогого порядка 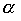 произведение
произведение
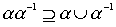
есть полное отношение. Достаточным условием является, например, такое.
Теорема 3.5. Если 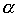 and
and 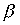 - строгие порядки и выполнены соотношения
- строгие порядки и выполнены соотношения
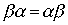 ,
,
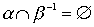 ,
,
то 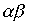 - строгий порядок.
- строгий порядок.
В данной лекции мы рассмотрели определения, разновидности и свойства отношений порядка. Однако, при этом не был затронут достаточно важный вопрос, как на практике строить отношения порядка? Этой проблемой занимаются такие разделы математики как теория выбора и принятия решений, теория голосования в больших и малых группах. Указанный вопрос мы рассмотрим в одной из следующих лекций.
1. Пухначев Ю., Попов Ю. Математика без формул. - М.: АО "Столетие", 1995.
2. Birkhoff G., Barti T. Modern applied algebra. - M .: Mir, 1976.
3. Schrader Yu. A. Equality, similarity, order. - M .: Science, 1971.
4. Nefedov V.N., Osipova V.A. The Course of Discrete Mathematics. - M .: Publishing house of MAI, 1992.
Je. P. Emelchenkov, V. Je. Emelchenkov
THE BINARY RELATIONS. RELATIONS OF ORDER
Abstract. The relation of the order and its characteristics are considered in the a rticle.
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.