Lecture
For arbitrary sets A, B, and C, the following relations are true (Table 1):
Table 1
1. Commutativity of association
| one'. Commutation intersection
|
2. Associativity of association
| 2 '. Associativity of intersection
|
3. Distribution of the union relative to the intersection
| 3 '. Distribution of intersection with respect to the union
|
4. The laws of action with empty and universal sets
| four'. Laws of action with empty and universal sets
|
5. The law of idempotency of the association
| five'. The law of idempotency of intersection
|
6. Law de Morgan
| 6 '. Law de Morgan
|
7. The law of absorption
| 7 '. Absorption law
|
8. The law of gluing
| eight'. Gluing law
|
9. Law of Poretsky
| 9'. Poretsky's law
|
10. The law of double addition
| |
Example 6
Prove the following identity 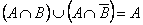 .
.
Decision.
Let us prove this identity in two ways: analytically (using the equivalences of the algebra of sets) and constructively (using the Euler-Venn diagrams).
one. 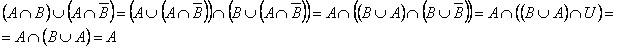
2. Construct the corresponding Euler-Venn diagrams (Fig. 7).
|


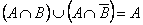
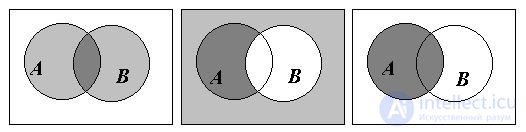 |
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.