Here are collected definitions of terms from graph theory. Italicized links to terms in this dictionary (on this page).
|
|
|
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
|
BUT
- Automorphism - Isomorphism of a graph with itself.
- Acyclic graph - a graph without cycles .
B
- Bigraph - see bichromatic graph .
- Block - graph without hinges .
- A block design with parameters (v, k, λ) is a covering with the multiplicity λ of a complete graph on v vertices, complete graphs on k vertices.
AT
- Vertex valence - see vertex degree .
- Vertex , Node is a basic concept: a point where edges and / or arcs can converge / exit. The set of vertices of a graph G is denoted by V (G).
- Edge weight is a value assigned to a given edge of a weighted graph . Usually, the weight is a real number, in which case it can be interpreted as the “length” of the edge.
- A weighted graph is a graph, each edge of which is associated with a certain value ( edge weight ).
- A hanging vertex is a vertex whose degree is 1 (i.e.
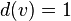 ).
). - A completely disconnected graph ( empty graph , null-graph ) is a regular graph of degree 0, that is, a graph without edges .
- The height of the tree is the maximum length of the path from the root to the leaf .
R
- Hamiltonian graph - a graph in which there is a Hamiltonian cycle .
- Hamiltonian path - a simple path in a graph that contains all the vertices of the graph exactly once.
- A Hamiltonian cycle is a simple cycle in a graph containing all the vertices of the graph exactly once.
- A geometric implementation is a figure whose vertices correspond to the vertices of the graph, and the edges — the edges of the graph and the edges in the figure connect the vertices corresponding to the vertices in the graph.
- A geometric graph is a flat figure of vertices — points of the plane and edges — lines connecting some pairs of vertices. Any graph can represent in many ways.
- A hypergraph is a collection of a set of vertices and a set of hyperhangs (a subset of the n-th Euclidean degree of the set of vertices, that is, a hyperface connects an arbitrary number of vertices).
- Homeomorphic graphs are graphs obtained from a single graph using a sequence of subdivisions of edges.
- A face is an area bounded by edges in a flat graph and not containing within itself vertices and edges of the graph. The outer part of the plane also forms a face.
- Graph is a basic concept. Includes a set of vertices and a set of edges , which is a subset of the Cartesian square of the set of vertices (that is, each edge connects exactly two vertices).
- A graph of genus g is a graph that can be represented without intersections on the surface of the genus g and cannot be represented without intersections on any surface of the genus g -1. In particular, planar graphs are of genus 0.
D
- Dual graph . A graph A is called dual to a planar graph B if the vertices of A correspond to the faces of B and two vertices of A are joined by an edge if and only if the corresponding faces of B have at least one common edge.
- The bichromatic graph (or biggraph , or even graph ) is a graph
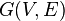 such that the set of vertices of V is divided into two disjoint subsets
such that the set of vertices of V is divided into two disjoint subsets 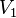 and
and 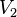 and moreover, every edge E is incident to the vertex of
and moreover, every edge E is incident to the vertex of 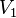 and the top of
and the top of 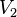 (i.e. connects the top of
(i.e. connects the top of 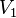 with top of
with top of 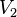 ). That is, the correct coloring of the graph in two colors. Sets
). That is, the correct coloring of the graph in two colors. Sets 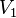 and
and 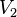 are called “shares” of a bipartite graph. A bipartite graph is called “complete” if any two vertices of
are called “shares” of a bipartite graph. A bipartite graph is called “complete” if any two vertices of 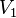 and
and 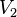 are adjacent. If a
are adjacent. If a 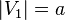 ,
, 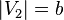 , then a full bicarbonated graph is denoted
, then a full bicarbonated graph is denoted 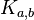 .
. - A doubly connected graph is a connected graph with no hinges .
- A tree is a connected graph that does not contain cycles .
- The diameter of the graph
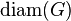 Is the maximum distance between vertices for all pairs of vertices. The distance between the vertices is the smallest number of edges of the path connecting the two vertices.
Is the maximum distance between vertices for all pairs of vertices. The distance between the vertices is the smallest number of edges of the path connecting the two vertices. - The length of the route - the number of edges in the route (with repetitions). If route
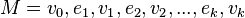 , then the length of M is equal to k (denoted by
, then the length of M is equal to k (denoted by 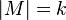 ).
). - Path length - the number of path arcs (or the sum of the lengths of its arcs, if the latter are given). So for the path v 1 , v 2 , ..., v n the length is equal to n-1.
- The arc is an oriented edge .
- Addition of a graph is a graph over the same set of vertices as the original one, but vertices are connected by an edge if and only if there is no edge in the original graph.
H
- Earl Star is a complete bichromatic graph
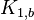 .
.
AND
- An isolated vertex is a vertex whose degree is 0 (that is, there are no edges incident to it).
- Isomorphism Two graphs are called isomorphic if there is a permutation of the vertices for which they coincide. In other words, two graphs are called isomorphic if there is a one-to-one correspondence between their vertices and edges, which preserves contiguity and incidence (the graphs differ only in the names of their vertices).
- The invariant of the graph is a numerical characteristic of the graph or their ordered vector, which characterizes the structure of the graph invariantly with respect to the renumbering of the vertices.
- An interval graph is a graph whose vertices can be one-to-one mapped to segments on the real axis in such a way that two vertices are incident to one edge if and only if the segments corresponding to these vertices intersect.
- Incidence is a concept used only in relation to an edge and a vertex: if
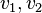 - tops, and
- tops, and 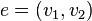 - connecting edge, then vertex
- connecting edge, then vertex 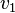 and rib
and rib  incident top
incident top 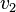 and rib
and rib  also incident. Two vertices (or two edges) cannot be incident. The notion of adjacency is used to designate the nearest vertices (edges).
also incident. Two vertices (or two edges) cannot be incident. The notion of adjacency is used to designate the nearest vertices (edges).
TO
- A cell is a regular graph of the smallest girth for a given degree of vertices.
- A clique is a subset of vertices of a graph that are completely connected to each other, that is, a subgraph that is a complete graph .
- Clique number (Eng. Clique number) - the number (G) of the vertices in the greatest click. Other names - density, density.
- Maximum click - click with the maximum possible number of vertices among the click graph.
- A wheel - (denoted by W n ) is a graph with n vertices (n ≥ 4) formed by connecting a single vertex with all vertices of the ( n -1) -cycle.
- Constructive enumeration of graphs - getting a complete list of graphs in a given class.
- A connected component of a graph is a subset of the vertices of the graph such that for any two vertices from this set there is a path from one to another, and there is no path from the vertex of this set to a vertex not from this set.
- A component of a strongly connected graph , a layer is the maximum set of vertices of an oriented graph such that for any two vertices of this set there is a path from both the first to the second and the second to the first.
- The contour is a closed path in the digraph .
- The root of the tree is the selected top of the tree; in digraph there is a vertex with zero degree of entry.
- A cocycle is a minimal cut , the minimal set of edges, the removal of which makes the graph disconnected.
- Multiple edges - several edges incident to the same pair of vertices. They are found in multigraphs .
- A cubic graph is a regular graph of degree 3, that is, a graph in which each vertex is incidentally exactly three edges.
- A k-longitudinal graph is a G graph whose chromatic number is c (G) = k
- A k-connected graph is a connected graph in which there is no set
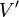 of
of 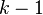 or fewer vertices , such that deleting all vertices
or fewer vertices , such that deleting all vertices 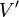 and the edges incident to them breaks the connectedness of the graph. In particular, a connected graph is 1-connected, and a doubly connected one is 2-connected.
and the edges incident to them breaks the connectedness of the graph. In particular, a connected graph is 1-connected, and a doubly connected one is 2-connected.
L
- A Lamine graph with n vertices is a graph G such that, firstly, for each k, any subgraph of G that contains k vertices has no more than 2 k −3 edges and, second, a graph G has exactly 2 n −3 edges.
- A forest is an undirected graph without cycles. The components of the connectivity of the forest are trees .
- A tree leaf is the top of a tree with a single edge or incoming arc .
- The local degree of a vertex is the number of edges incident to it. The loop makes a contribution equal to "2" to the power of the vertex.
M
- Maxi code
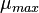 - a hard-to-calculate complete invariant of the graph, obtained by writing the binary values of the adjacency matrix into a line with the subsequent translation of the resulting binary number into decimal form. Maxi-code corresponds to the sequence of rows and columns, in which the resulting value is the maximum possible.
- a hard-to-calculate complete invariant of the graph, obtained by writing the binary values of the adjacency matrix into a line with the subsequent translation of the resulting binary number into decimal form. Maxi-code corresponds to the sequence of rows and columns, in which the resulting value is the maximum possible. - Maximum matching in the graph. A matching is called maximal if any other matching contains a smaller number of edges.
- The route in the graph is an alternating sequence of vertices and edges.
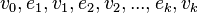 in which any two adjacent elements are incident . If a
in which any two adjacent elements are incident . If a 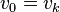 , the route is closed , otherwise open .
, the route is closed , otherwise open . - The reachability matrix of a digraph is a matrix containing information about the existence of paths between vertices in a digraph.
- The incidence matrix of a graph is a matrix whose elemental values are characterized by the incidence of the corresponding vertices of the graph (vertically) and its edges (horizontally). For an undirected graph, an element takes the value 1 if the corresponding vertex and edge are incident. For a directed graph, an element takes the value 1 if the incident vertex is the beginning of an edge, a value -1 , if the incident vertex is the end of the edge; in other cases (including loops ) the value of the element is assigned 0 .
- The adjacency matrix of a graph is a matrix whose values of elements are characterized by the adjacency of the vertices of the graph. In this case, the value of the matrix element is assigned the number of edges that connect the corresponding vertices (that is, which are incident to both vertices). The loop is immediately considered two connections for the vertex, that is, the value of the matrix element in this case should be added 2 .
- Mini code
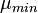 - a hard-to-calculate complete invariant of the graph, obtained by writing the binary values of the adjacency matrix into a line with the subsequent translation of the resulting binary number into decimal form. Mini-code corresponds to the order of rows and columns, in which the resulting value is the minimum possible.
- a hard-to-calculate complete invariant of the graph, obtained by writing the binary values of the adjacency matrix into a line with the subsequent translation of the resulting binary number into decimal form. Mini-code corresponds to the order of rows and columns, in which the resulting value is the minimum possible. - The minimal skeleton (or Minimum weight skeleton , Minimum spanning tree ) of a graph is an acyclic (not having cycles) set of edges in a connected, weighted and undirected graph connecting all the vertices of this graph, and the sum of the weights of all the edges in it is minimal.
- The adjacency set of a vertex v is the set of vertices adjacent to the vertex v . Denoted by
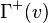
- The minor of a graph is a graph that can be obtained from the original by deleting and tightening the arcs.
- A bridge is an edge whose removal increases the number of connected components in a graph.
- A multigraph is a graph in which there can be a pair of vertices, which is connected by more than one edge (non-directional), or by more than two arcs of opposite directions.
H
- A directed graph is a directed graph in which two vertices are connected by no more than one arc.
- A directed acyclic graph is an oriented graph without contours .
- An independent set of vertices (also known as an internally stable set ) is a set of vertices of the graph G, such that any two vertices in it are non-adjacent (no pair of vertices is connected by an edge).
- An independent set is called maximal when there is no other independent set into which it would belong.
- If Q is a family of all independent sets of a graph G, then the number a (G) = max | S | (where S belongs to Q) is called the independence number of the graph G, and the set S * on which this maximum is reached is called the largest independent set .
- Independent vertices are pairwise non-adjacent vertices of a graph. [one]
- An inseparable graph is called a connected, non-empty graph with no articulation points. [2] .
- Normalized graph - oriented graph without cycles.
- A null graph (a completely disconnected graph , an empty graph ) is a regular graph of degree 0, that is, a graph that does not contain edges .
ABOUT
- Girth - the length of the smallest cycle in the graph.
- Combining graphs (labeled graphs
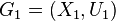 and
and 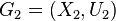 ) - Count
) - Count 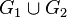 whose set of vertices is
whose set of vertices is 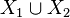 , and a set of edges -
, and a set of edges - 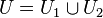 .
. - The neighborhood of order k is the set of vertices at a distance k from the given vertex v ; sometimes interpreted broadly as a set of vertices that are separated from v at a distance no more than k .
- An environment is a set of vertices adjacent to a given one.
- The orgraph , oriented graph G = (V, E) is a pair of sets, where V is the set of vertices (nodes), E is the set of arcs (oriented edges). An arc is an ordered pair of vertices (v, w), where the vertex v is called the beginning and w is the end of the arc. We can say that the arc v → w leads from the vertex v to the vertex w, while the vertex w is adjacent to the vertex v.
- Spanned tree ( skeleton ) of a (undirected) connected graph
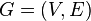 - any partial graph
- any partial graph 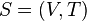 being a tree .
being a tree . - Spanned subgraph is a subgraph containing all vertices.
P
- Matching is a set of pairwise non-adjacent edges.
- A loop is a rib whose beginning and end are at the same vertex.
- Intersection of graphs (labeled graphs
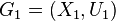 and
and 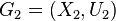 ) - Count
) - Count 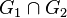 whose set of vertices is
whose set of vertices is 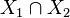 , and a set of edges -
, and a set of edges - 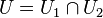 .
. - Enumeration of graphs - counting the number of non-isomorphic graphs in a given class (with given characteristics).
- A peripheral vertex is a vertex whose eccentricity is equal to the diameter of the graph.
- A planar graph is a graph that can be drawn ( laid ) on a plane without intersecting edges. Is isomorphic to a flat graph, that is, is a graph with intersections, but allowing it to be flat, therefore it may differ from a flat graph in an image on a plane. Thus, there may be a difference between a planar graph and a planar graph when imaged on a plane.
- A flat graph is a geometric graph in which no two edges have common points, except for the vertices incident to both of them (do not intersect). It is a laid graph on the plane.
- The subgraph of the original graph is a graph containing a certain subset of the vertices of the given graph and a certain subset of edges incident to them. (cf. Sugraph .) With respect to the subgraph, the initial graph is called the supergraph.
- A complete graph is a graph in which for each pair of vertices
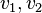 , there is an edge incident
, there is an edge incident 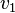 and incident
and incident 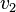 (each vertex is connected by an edge with any other vertex).
(each vertex is connected by an edge with any other vertex). - The complete invariant of a graph is a numerical characteristic of a graph or their ordered vector, the values of which are necessary and sufficient to establish the isomorphism of graphs.
- A full bipartite graph is a bipartite graph in which each vertex of one subset is connected by an edge with each vertex of another subset.
- Degree of entry in the digraph for the vertex
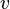 - the number of arcs entering the vertex. Denoted by
- the number of arcs entering the vertex. Denoted by 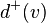 ,
, 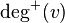 ,
, 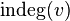 or
or 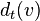 .
. - Degree of outcome in the digraph for the vertex
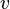 - the number of arcs emanating from the vertex. Denoted by
- the number of arcs emanating from the vertex. Denoted by 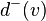 ,
, 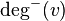 ,
, 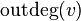 or
or 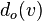 .
. - A marked graph is a graph whose vertices or arcs are assigned some labels, for example, natural numbers or symbols of some alphabet.
- The generated subgraph is a subgraph generated by the set of edges of the original graph. It does not necessarily contain all the vertices of the graph, but these vertices are connected by the same edges as in the graph.
- The order of the graph is the number of vertices of the graph. [3]
- The correct coloring of the graph is a coloring in which each color class is an independent set. In other words, in the correct coloring, any two adjacent vertices must have different colors.
- Graph product - for graph data
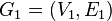 and
and 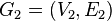 the product is a graph
the product is a graph 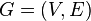 whose vertices
whose vertices 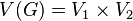 are the Cartesian product of the vertex sets of the original graphs.
are the Cartesian product of the vertex sets of the original graphs. - A simple chain is a route in which all vertices are different.
- A simple graph is a graph with no multiple edges and loops .
- A simple path is a path whose edges all are pairwise distinct [4] . In other words, a simple path does not pass through one edge twice.
- A simple loop is a loop that does not pass through one vertex twice.
- A pseudograph is a graph that can contain loops and / or multiple edges.
- Пустой граф ( вполне несвязный граф , нуль-граф ) — регулярный граф степени 0, то есть граф, не содержащий рёбер.
- Путь — последовательность рёбер (в неориентированном графе) и/или дуг (в ориентированном графе), такая, что конец одной дуги (ребра) является началом другой дуги (ребра). Или последовательность вершин и дуг (рёбер) в которой каждый элемент инцидентен предыдущему и последующему [4] . Может рассматриваться как частный случай маршрута .
- Путь в орграфе — это последовательность вершин v 1 , v 2 , …, v n , для которой существуют дуги v 1 → v 2 , v 2 → v 3 , …, v n-1 → v n . Говорят, что этот путь начинается в вершине v 1 , проходит через вершины v 2 , v 3 , …, v n-1 , и заканчивается в вершине v n .
R
- Радиус графа — минимальный из эксцентриситетов вершин связного графа; вершина, на которой достигается этот минимум, называется центральной вершиной.
- Разбиение графа — представление исходного графа в виде множества подмножеств вершин по определенным правилам.
- Разделяющая вершина — то же, что и шарнир и точка сочленения .
- Развёртка графа — функция, заданная на вершинах ориентированного графа.
- Размеченный граф — граф, для которого задано множество меток S, функция разметки вершин f : A → S и функция разметки дуг g : R → S. Графически эти функции представляются надписыванием меток на вершинах и дугах. Множество меток может разделяться на два непересекающихся подмножества меток вершин и меток дуг.
- Разрез — множество рёбер , удаление которого делает граф несвязным.
- Рамочный граф — граф, который можно нарисовать на плоскости таким способом, что любая ограниченная грань является четырёхугольником и любая вершина с тремя и менее соседями инцидентна неограниченной грани. [five]
- Раскраска графа — разбиение вершин на множества (называемые цветами). Если при этом нет двух смежных вершин принадлежащих одному и тому же множеству (то есть две смежные вершины всегда разного цвета), то такая раскраска называется правильной.
- Расстояние между вершинами — длина кратчайшей цепи (в орграфе пути), соединяющей заданные вершины. Если такой цепи (пути) не существует, расстояние полагается равным бесконечности.
- Ребро — базовое понятие. Ребро соединяет две вершины графа.
- Регулярный граф — граф, степени всех вершин которого равны. Степень регулярности является инвариантом графа и обозначается
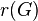 . Для нерегулярных графов
. Для нерегулярных графов 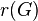 не определено. Регулярные графы представляют особую сложность для многих алгоритмов.
не определено. Регулярные графы представляют особую сложность для многих алгоритмов. - Регулярный граф степени 0 ( вполне несвязный граф , пустой граф , нуль-граф ) — граф без рёбер .
WITH
- Самодвойственный граф — граф, изоморфный своему двойственному графу .
- Связность . Две вершины в графе связаны , если существует соединяющая их (простая) цепь .
- Связный граф — граф, в котором все вершины связаны.
- Сечение графа — множество рёбер, удаление которых делит граф на два изолированных подграфа, один из которых, в частности, может быть тривиальным графом.
- Сеть — в принципе, то же, что и граф , хотя сетями обычно называют графы, вершины которых определённым образом помечены.
- Ориентированная сеть — ориентированный граф, не содержащий контуров.
- Сильная связность . Две вершины в ориентированном графе сильно связаны , если существует путь из первой во вторую и из второй в первую.
- Сильно связный орграф — орграф , в котором все вершины сильно связаны.
- Смежность — понятие, используемое в отношении только двух рёбер либо только двух вершин : Два ребра, инцидентные одной вершине, называются смежными ; две вершины, инцидентные одному ребру, также называются смежными . (ср. Инцидентность .)
- Смешанный граф — граф, содержащий как ориентированные, так и неориентированные рёбра .
- Совершенное паросочетание — паросочетание, содержащее все вершины графа.
- Соединением двух графов
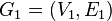 and
and 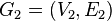 , не имеющих общих вершин, называется граф
, не имеющих общих вершин, называется граф 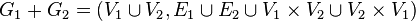 . [6]
. [6]
Из определения видно, что соединение графов обладает свойствами коммутативности и ассоциативности
- Спектр графа — множество всех собственных значений матрицы смежности с учётом кратных рёбер.
- Степень вершины — количество рёбер графа G , инцидентных вершине x . Обозначается
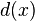 . Минимальная степень вершины графа G обозначается
. Минимальная степень вершины графа G обозначается 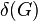 . а максимальная —
. а максимальная — 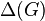 .
. - Стягивание ребра графа — замена концов ребра одной вершиной, соседями новой вершины становятся соседи этих концов. Graph
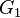 стягиваем к
стягиваем к 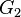 , если второй можно получить из первого последовательностью стягиваний рёбер.
, если второй можно получить из первого последовательностью стягиваний рёбер. - Суграф ( частичный граф ) исходного графа — граф, содержащий все вершины исходного графа и подмножество его рёбер . (ср. Подграф .)
- Суперграф — это любой граф, содержащий исходный граф (то есть, для которого исходный граф является подграфом )
T
- Тождественный граф — граф, у которого возможен один единственный автоморфизм — тождественный. Образно говоря, тождественный граф — это «абсолютно несимметричный» граф.
- Точка сочленения — то же, что и шарнир и разделяющая вершина .
- Триангуляция поверхности — укладка графа на поверхность, разбивающая её на треугольные области; частный случай топологической триангуляции.
- Тривиальный граф — граф, состоящий из одной вершины .
- Турнир — ориентированный граф , в котором каждая пара вершин соединена одним ребром.
Have
- Узел — то же, что и Вершина .
- Укладка : граф укладывается на некоторой поверхности, если его можно нарисовать на этой поверхности так, чтобы рёбра графа при этом не пересекались. (См. Планарный граф , Плоский граф .)
- Упорядоченный граф — граф, в котором рёбра, выходящие из каждой вершины, однозначно пронумерованы, начиная с 1. Рёбра считаются упорядоченными в порядке возрастания номеров. При графическом представлении часто рёбра считаются упорядоченными в порядке некоторого стандартного обхода (например,против часовой стрелки).
F
- n-Фактор графа — регулярный остовный подграф степени
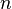 .
. - n-Факторизация графа — разбиение графа на независимые n-факторы .
X
- Хроматическое число графа — минимальное количество цветов, требуемое для раскраски вершин графа, при которой любые вершины, соединенные ребром, раскрашены в разные цвета.
- Характеристический многочлен графа— это характеристический многочлен его матрицы смежности.
C
- Центр графа — множество вершин
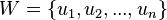 , для которых справедливо равенство:
, для которых справедливо равенство: 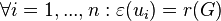 where
where  — это эксцентриситет вершины, а
— это эксцентриситет вершины, а  — радиус графа.
— радиус графа. - Цепь в графе — маршрут , все рёбра которого различны. Если все вершины (а тем самым и рёбра) различны, то такая цепь называется простой ( элементарной ). В цепи
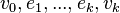 tops
tops 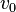 and
and 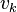 называются концами цепи. Цепь с концами u и v соединяет вершины u и v . Цепь, соединяющая вершины u и v обозначается
называются концами цепи. Цепь с концами u и v соединяет вершины u и v . Цепь, соединяющая вершины u и v обозначается 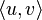 . Для орграфов цепь называется орцепью.
. Для орграфов цепь называется орцепью. - В некоторых источниках простая цепь — цепь, рёбра которой различны, что является более слабым условием.
- Цикл — замкнутая цепь . Для орграфов цикл называется контуром .
- Цикл ( простой цикл ) в орграфе — это простой путь длины не менее 1, который начинается и заканчивается в одной и той же вершине.
- Цикл Гамильтона — то же, что и Гамильтонов цикл .
- Цикломатическое число графа — минимальное число рёбер, которые надо удалить, чтобы граф стал ациклическим. Для связного графа существует соотношение:
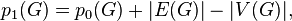 Where
Where 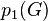 — цикломатическое число,
— цикломатическое число, 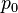 — число компонент связности графа,
— число компонент связности графа, 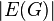 — число рёбер , а
— число рёбер , а 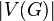 — число вершин .
— число вершин .
H
- Частичный граф — то же, что и суграф .
- Чётный граф — то же, что и двудольный граф .
Sh
- Шарнир — вершина графа , в результате удаления которой вместе со всеми инцидентными ей рёбрами количество компонент связности в графе возрастает.
- Шестерёнка (обозначается
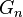 ) — граф, получаемый из колеса путём размещения дополнительных вершин между каждой парой смежных вершин периметра. Шестерёнки принадлежат семейству рамочных графов и играют важную роль при описании запрещённых подграфов рамочных графов [7]
) — граф, получаемый из колеса путём размещения дополнительных вершин между каждой парой смежных вершин периметра. Шестерёнки принадлежат семейству рамочных графов и играют важную роль при описании запрещённых подграфов рамочных графов [7]
Uh
- Эйлеров граф — это граф, в котором существует цикл , содержащий все рёбра графа по одному разу (вершины могут повторяться).
- The Euler chain (or Euler cycle ) is a chain ( cycle ) that contains all the edges of the graph (the vertices can be repeated).
- The eccentricity of a vertex is the maximum distance from all minimal distances from other vertices to a given vertex.
- An elementary path is a path whose vertices, with the exception of, perhaps, the first and the last, are different. In other words, a simple path does not go through one vertex twice, but it can begin and end at the same vertex, in which case it is called a cycle (an elementary cycle).
- An elementary procedure is called the following procedure: we take an edge (together with the vertices incident to it, for example, u and v) and “tighten” it, that is, we delete the edge and identify the vertices u and v. The resulting vertex is incident to the edges (other than), which were originally incident to u or v.
Links
- Explanatory dictionary on graph theory
- Graph theory
- ↑ Distel R. Graph Theory Per. from English - Novosibirsk: Publishing house of the Institute of mathematics, 2002. - p. 17.
- ↑ Harari F. Graph Theory. - M .: Mir, 1972. - p. 41.
- ↑ Distel R. Graph Theory Per. from English - Novosibirsk: Publishing house of the Institute of mathematics, 2002. - p. 16.
- ↑ Go to: 1 2 Kuznetsov O. P., Adelson-Velsky G. M. / Discrete Mathematics for the Engineer. / M .: Energy, 1980-344 p., Il. Page 120-122
- ↑ A.V. Karzanov, Extensions of finite metrics and the problem of equipment placement, Proceedings of the ISA RAS . - 2007. - T. 29. - p. 225-244 (241).
- ↑ M. B. Abrosimov On minimal vertex 1-extensions of compounds of graphs of a special type. // Applied graph theory. . - 2011. - V. 4.
- ↑ H.-J. Bandelt, V. Chepoi, D. Eppstein, Combinatorics and Geometry of Finite and Infinite squaregraphs // SIAM Journal on Discrete Mathematics . - 2010. - V. 4. - T. 24. - p. 1399–1440. —DOI: 10.1137 / 090760301 - arΧiv: 0905.4537.
Literature
- Distel R. Graph Theory Trans. from English - Novosibirsk: Publishing House of the Inst. Of Mathematics, 2002.- 336c.
- Harari F. Graph Theory. - M .: URSS, 2003. - 300 p. - ISBN 5-354-00301-6.
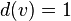 ).
). 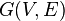 such that the set of vertices of V is divided into two disjoint subsets
such that the set of vertices of V is divided into two disjoint subsets 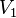 and
and 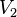 and moreover, every edge E is incident to the vertex of
and moreover, every edge E is incident to the vertex of 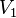 and the top of
and the top of 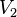 (i.e. connects the top of
(i.e. connects the top of 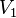 with top of
with top of 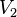 ). That is, the correct coloring of the graph in two colors. Sets
). That is, the correct coloring of the graph in two colors. Sets 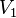 and
and 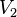 are called “shares” of a bipartite graph. A bipartite graph is called “complete” if any two vertices of
are called “shares” of a bipartite graph. A bipartite graph is called “complete” if any two vertices of 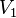 and
and 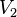 are adjacent. If a
are adjacent. If a 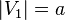 ,
, 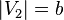 , then a full bicarbonated graph is denoted
, then a full bicarbonated graph is denoted 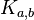 .
. 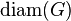 Is the maximum distance between vertices for all pairs of vertices. The distance between the vertices is the smallest number of edges of the path connecting the two vertices.
Is the maximum distance between vertices for all pairs of vertices. The distance between the vertices is the smallest number of edges of the path connecting the two vertices. 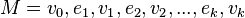 , then the length of M is equal to k (denoted by
, then the length of M is equal to k (denoted by 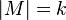 ).
). 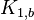 .
. 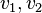 - tops, and
- tops, and 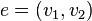 - connecting edge, then vertex
- connecting edge, then vertex 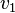 and rib
and rib  incident top
incident top 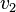 and rib
and rib  also incident. Two vertices (or two edges) cannot be incident. The notion of adjacency is used to designate the nearest vertices (edges).
also incident. Two vertices (or two edges) cannot be incident. The notion of adjacency is used to designate the nearest vertices (edges). 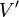 of
of 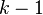 or fewer vertices , such that deleting all vertices
or fewer vertices , such that deleting all vertices 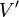 and the edges incident to them breaks the connectedness of the graph. In particular, a connected graph is 1-connected, and a doubly connected one is 2-connected.
and the edges incident to them breaks the connectedness of the graph. In particular, a connected graph is 1-connected, and a doubly connected one is 2-connected. 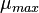 - a hard-to-calculate complete invariant of the graph, obtained by writing the binary values of the adjacency matrix into a line with the subsequent translation of the resulting binary number into decimal form. Maxi-code corresponds to the sequence of rows and columns, in which the resulting value is the maximum possible.
- a hard-to-calculate complete invariant of the graph, obtained by writing the binary values of the adjacency matrix into a line with the subsequent translation of the resulting binary number into decimal form. Maxi-code corresponds to the sequence of rows and columns, in which the resulting value is the maximum possible. 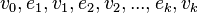 in which any two adjacent elements are incident . If a
in which any two adjacent elements are incident . If a 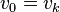 , the route is closed , otherwise open .
, the route is closed , otherwise open . 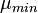 - a hard-to-calculate complete invariant of the graph, obtained by writing the binary values of the adjacency matrix into a line with the subsequent translation of the resulting binary number into decimal form. Mini-code corresponds to the order of rows and columns, in which the resulting value is the minimum possible.
- a hard-to-calculate complete invariant of the graph, obtained by writing the binary values of the adjacency matrix into a line with the subsequent translation of the resulting binary number into decimal form. Mini-code corresponds to the order of rows and columns, in which the resulting value is the minimum possible. 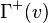
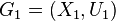 and
and 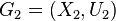 ) - Count
) - Count 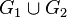 whose set of vertices is
whose set of vertices is 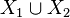 , and a set of edges -
, and a set of edges - 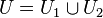 .
. 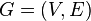 - any partial graph
- any partial graph 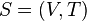 being a tree .
being a tree . 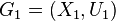 and
and 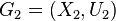 ) - Count
) - Count 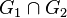 whose set of vertices is
whose set of vertices is 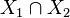 , and a set of edges -
, and a set of edges - 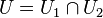 .
. 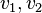 , there is an edge incident
, there is an edge incident 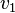 and incident
and incident 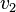 (each vertex is connected by an edge with any other vertex).
(each vertex is connected by an edge with any other vertex). 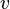 - the number of arcs entering the vertex. Denoted by
- the number of arcs entering the vertex. Denoted by 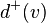 ,
, 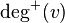 ,
, 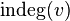 or
or 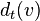 .
. 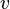 - the number of arcs emanating from the vertex. Denoted by
- the number of arcs emanating from the vertex. Denoted by 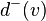 ,
, 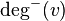 ,
, 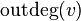 or
or 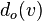 .
. 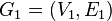 and
and 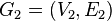 the product is a graph
the product is a graph 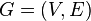 whose vertices
whose vertices 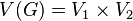 are the Cartesian product of the vertex sets of the original graphs.
are the Cartesian product of the vertex sets of the original graphs.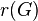 . Для нерегулярных графов
. Для нерегулярных графов 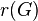 не определено. Регулярные графы представляют особую сложность для многих алгоритмов.
не определено. Регулярные графы представляют особую сложность для многих алгоритмов. 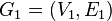 and
and 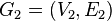 , не имеющих общих вершин, называется граф
, не имеющих общих вершин, называется граф 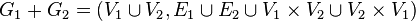 . [6]
. [6] 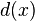 . Минимальная степень вершины графа G обозначается
. Минимальная степень вершины графа G обозначается 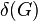 . а максимальная —
. а максимальная — 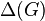 .
. 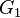 стягиваем к
стягиваем к 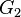 , если второй можно получить из первого последовательностью стягиваний рёбер.
, если второй можно получить из первого последовательностью стягиваний рёбер. 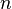 .
. 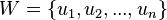 , для которых справедливо равенство:
, для которых справедливо равенство: 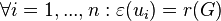 where
where  — это эксцентриситет вершины, а
— это эксцентриситет вершины, а  — радиус графа.
— радиус графа. 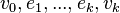 tops
tops 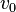 and
and 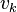 называются концами цепи. Цепь с концами u и v соединяет вершины u и v . Цепь, соединяющая вершины u и v обозначается
называются концами цепи. Цепь с концами u и v соединяет вершины u и v . Цепь, соединяющая вершины u и v обозначается 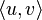 . Для орграфов цепь называется орцепью.
. Для орграфов цепь называется орцепью. 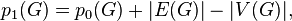 Where
Where 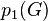 — цикломатическое число,
— цикломатическое число, 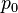 — число компонент связности графа,
— число компонент связности графа, 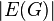 — число рёбер , а
— число рёбер , а 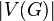 — число вершин .
— число вершин . 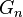 ) — граф, получаемый из колеса путём размещения дополнительных вершин между каждой парой смежных вершин периметра. Шестерёнки принадлежат семейству рамочных графов и играют важную роль при описании запрещённых подграфов рамочных графов [7]
) — граф, получаемый из колеса путём размещения дополнительных вершин между каждой парой смежных вершин периметра. Шестерёнки принадлежат семейству рамочных графов и играют важную роль при описании запрещённых подграфов рамочных графов [7]
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.