Connected graph, Non-connected graph, strongly connected graph of definition and theorem

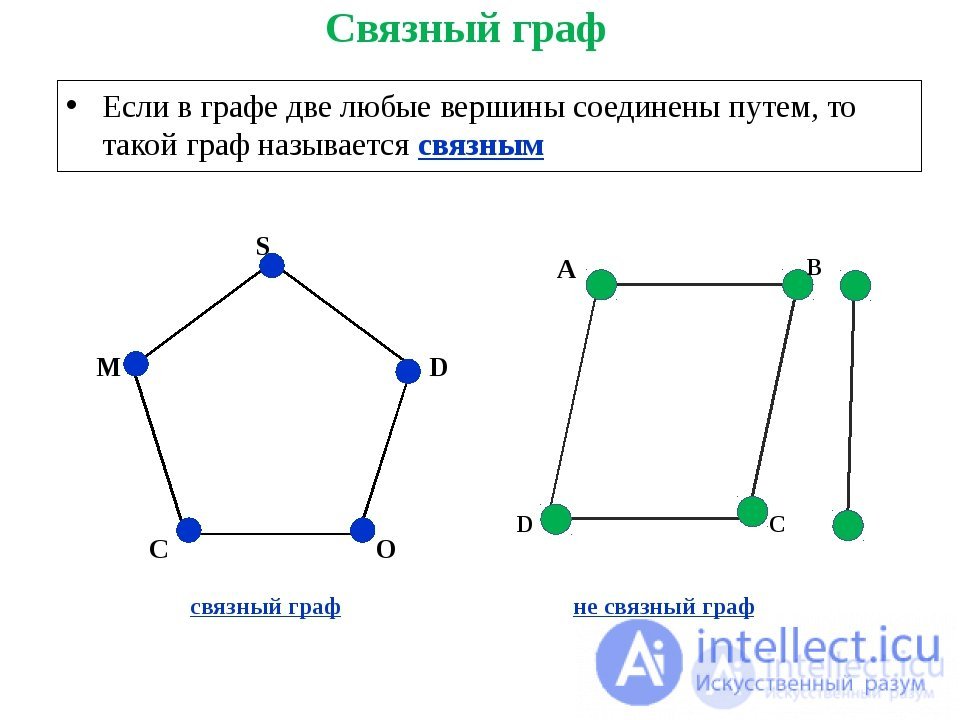
A connected graph is a graph containing exactly one connected component. This means that there is at least one path between any pair of vertices of this graph.

Content

• 1 Application examples
• 2 Connectivity for oriented graphs
• 3 Some criteria for connectivity
• 4 See also

Application examples

A direct application of graph theory is the theory of networks — and its application — the theory of electronic networks. For example, all computers connected to the Internet form a connected graph, and although a single pair of computers may not be connected directly (in the wording for graphs, not be connected by an edge), you can transfer information to any other computer from any computer vertices of the graph in any other).

Connectivity for directed graphs

In oriented graphs, several concepts of connectedness are distinguished.

An oriented graph is said to be strongly connected if there exists a (oriented) path from any vertex to any other, or, equivalently, the graph contains exactly one strongly connected component.

A directed graph is said to be weakly connected if the unoriented graph obtained from it is replaced by a replacement of oriented edges with an undirected one.

Some connectivity criteria

Here are some criterion (equivalent) definitions of a connected graph:
A graph is said to be simply connected (connected) if:

1. It has one connected component.
2. There is a path from any vertex to any other vertex.
3. There is a path from a given vertex to any other vertex.
4. Contains a connected subgraph that includes all vertices of the original graph
5. Contains as a subgraph a tree that includes all the vertices of the original graph (such a tree is called a spanner)
6. When arbitrarily dividing its vertices into 2 groups, there is always at least 1 edge connecting a pair of vertices from different groups.

Strongly connected graphs and graph components

A directed graph is called strongly connected or strong if for any two different vertices Xi and Xj there is at least one path connecting Xi with XjThis definition also means that any two vertices of such a graph are mutually reachable.

See also

• Menger's theorem