Lecture
Attainability matrix of a simple oriented graph 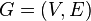 - binary closure matrix for relation transitivity
- binary closure matrix for relation transitivity 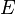 (it is given by the adjacency matrix of the graph). Thus, information about the existence of paths between vertices of a digraph is stored in the reachability matrix.
(it is given by the adjacency matrix of the graph). Thus, information about the existence of paths between vertices of a digraph is stored in the reachability matrix.
Let a simple graph be given 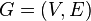 whose adjacency matrix is
whose adjacency matrix is 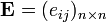 where
where 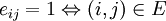 . The adjacency matrix provides information on all paths of length 1 (that is, the edges) in an ograph. To search for paths of length 2 you can find the composition of the relationship
. The adjacency matrix provides information on all paths of length 1 (that is, the edges) in an ograph. To search for paths of length 2 you can find the composition of the relationship 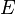 With myself:
With myself:
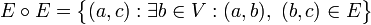 .
.
By definition, a relationship composition matrix 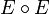 there is
there is 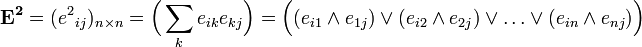 where
where 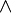 - conjunction, and
- conjunction, and 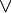 - disjunction.
- disjunction.
After finding the matrices 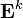 compositions
compositions 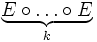 for all
for all 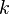 ,
, 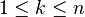 information on all paths of length from
information on all paths of length from 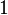 before
before 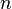 . So the matrix
. So the matrix 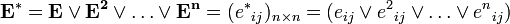 there is a desired reachability matrix.
there is a desired reachability matrix.
If boolean operations 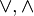 disjunctions and conjunctions replaced by ordinary algebraic operations
disjunctions and conjunctions replaced by ordinary algebraic operations 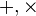 addition and multiplication respectively, finding the reachability matrix
addition and multiplication respectively, finding the reachability matrix 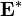 reduced to the usual step-by-step multiplication of matrices with the subsequent addition of the results of each step. Then the resulting matrix
reduced to the usual step-by-step multiplication of matrices with the subsequent addition of the results of each step. Then the resulting matrix 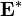 will consist not only of 0 and 1 and will characterize not only the presence of paths between the vertices, but already the number of such paths. In this case, you can allow the presence of multiple edges in the graph.
will consist not only of 0 and 1 and will characterize not only the presence of paths between the vertices, but already the number of such paths. In this case, you can allow the presence of multiple edges in the graph.
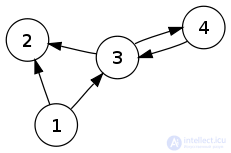
Consider a simple connected oriented graph 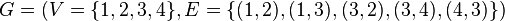 . It has an adjacency matrix.
. It has an adjacency matrix. 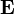 view:
view:
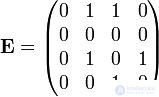
Find the boolean powers of this matrix. 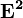 ,
, 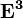 ,
, 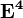 :
:
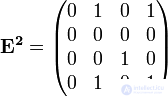 ,
, 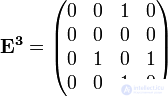 ,
, 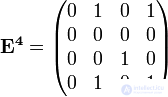 .
.
Get the reachability matrix
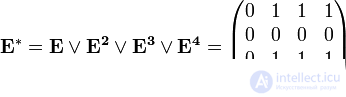
So from the top  You can get to any other.
You can get to any other.
When using algebraic operations, we get the matrix
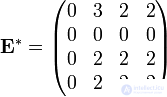
It shows the number of paths of length from 1 to 4 between the vertices of the digraph.
There is another algorithm for finding the reachability matrix exactly in 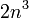 Steps - Worshel's algorithm.
Steps - Worshel's algorithm.
A strong connected matrix of a simple digraph is a binary matrix containing information about all strongly connected vertices in a digraph. The strong connected matrix is symmetric. For a strongly connected graph, such a matrix is filled with units.
A strong connectivity matrix can be constructed from a reachability matrix. Let be 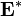 - matrix of reachability of the digraph
- matrix of reachability of the digraph 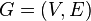 . Then the strong connectivity matrix
. Then the strong connectivity matrix 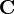 consists of elements
consists of elements 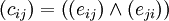 .
.
Consider the same graph as before.
Its reachability matrix is:
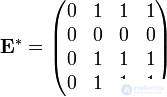
From it we get a strong connected matrix:
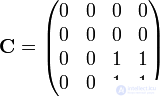
Vertices 3 and 4 are strongly connected with each other and with themselves.
For a connected graph, there is a notion of a connection matrix , similar to the reachability matrix.
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.