kograf, or additionally reducible graph, or P4-free graph

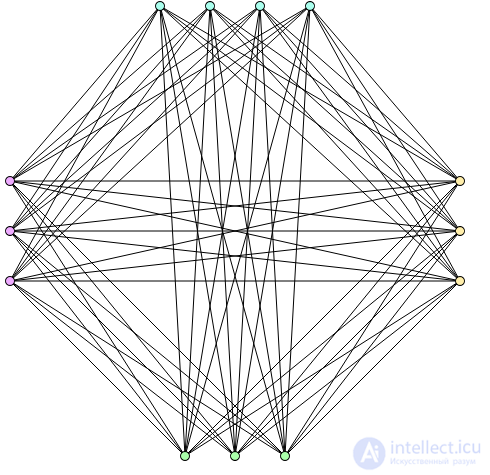
Graf Turana T (13,4) as an example of a kograf

In graph theory, a kograph , or an additionally reducible graph , or a graph free from P 4, is a graph that can be obtained from a graph with a single vertex K 1 by complementing and combining graphs. Thus, a family of cographers is the smallest class of graphs containing K 1 and closed with respect to addition and union.

Kografy opened independently by several authors, since the 1970s. The earliest references can be found in Yang (Jung 1978) , Lerchs (Lerchs 1971) , Zainshe (Seinsche 1974) and Sumner (Sumner 1974) . These graphs were called D * -graphs (Jung 1978) , hereditary Dacey graphs (after the work of James C. Dacey, Jr.) on orthomodular lattices. See Sumner 1974 ) and graphs with two descendants of Barlet and Uri (Burlet, Uhry 1984) .

See the book of Brandnstedt, Lee, and Spinrad (Brandstädt, Le, Spinrad 1999) , where coographers are discussed in more detail, including the facts presented here.

Definition and description

Any kograf can be built using the following rules:

1. Any single vertex of the graph is a cograph;
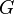2. If a - kograf, then its addition 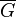also kograf;
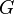3. If a and 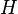- cographers, their unrelated association 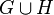also kograf.

Several other descriptions of cographers can be given. Among them:

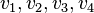• A kograf is a graph that does not contain a P 4 path with 4 vertices (that is, a length of 3) as a generated subgraph. Thus, a graph is a kograf if a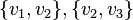nd only if, for any four vertices , if a and 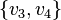- the edges of the graph, then at least one of or 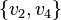is also a rib (Corneil, Lerchs, Burlingham 1981) .
• A kograf is a graph, all generated subgraphs of which have the property that any maximal clique intersects with any largest independent set at a single vertex.
• A kograf is a graph in which any nontrivial generated subgraph has at least two vertices with coincident neighborhoods.
• A kograf is a graph in which any connected generated subgraph has a disjoint complement.
• A kograf is a graph, for all connected generated subgraphs whose diameter does not exceed 2.
• A kograf is a graph in which any connected component is a distance-inherited graph [en] with a diameter not exceeding 2.
• A kograf is a graph with a click width [en] not exceeding 2 (Courcelle, Olariu 2000) .
• A kograf is a comparability graph of a series-parallel partial order [en] (Jung 1978) .
• A kograf is a permutation graph of a separable permutation [en] (Bose, Buss, Lubiw 1998) .

All full graphs, full bipartite graphs, threshold graphs and Turan graphs are co-graphs. Any kograf is a distance-inheritable perfect comparability graph.

Koderevya

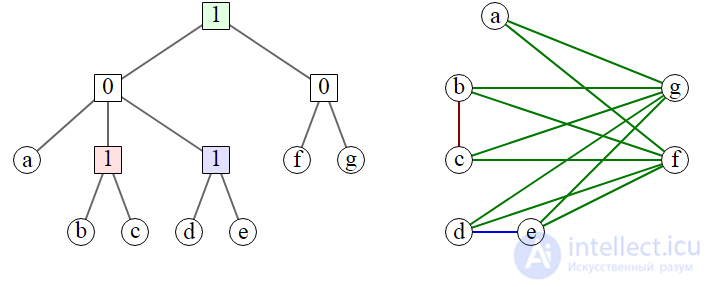
Codes and related kografy. Each edge ( u , v ) in a cograph has the corresponding color of the nearest common parent of the vertices u and v in the coder.

A Koderevo is a tree in which internal vertices are labeled with the numbers 0 and 1. Any code tree T defines a kograf G that has leaves of the Koderev T as vertices, and a subtree that has a root at T , corresponds to a generated subgraph in G defined by a set of descendants this vertex:

• A subtree consisting of a single leaf corresponds to a generated subgraph with a single vertex.
• The subtree with the root vertex labeled 0 corresponds to the union of the subgraphs formed by the descendants of the vertex.
• The subtree with the root vertex labeled 1 corresponds to the connection of subgraphs formed by the descendants of the vertex. That is, we form a union and add an edge between any two vertices corresponding to two leaves lying in different subtrees. You can also consider a compound as an addition to all graphs formed by combining an add-on, followed by building an addition to the result of the union.

The equivalent way to construct a kograf from a koderev is that two vertices are connected by an edge if and only if the smallest common ancestor of the corresponding leaves is marked 1. And vice versa, any kograf can be represented by a coder in this way. If we require that all the tags on all the chains from the root to the leaves alternate, such a presentation would be the only one (Corneil, Lerchs, Burlingham 1981) .

Computational properties [edit]

A cograph can be recognized in linear time and can be constructed as a coded-tree representation, if modular decomposition [en] (Corneil, Perl, Stewart 1985) , purification of decomposition [en] (Habib, Paul 2005) or splitting decomposition (Gioan, Paul 2008 ) . Once the codec has been built, many familiar problems of graph theory can be solved by going from the bottom up to the codec.

For example, to find the maximum click in a cograph, we calculate, passing from bottom to top, the maximum click in each subgraph represented by the subtree of the tree. For each vertex with label 0, the maximum click is the maximum click received from the descendants of the top. For a vertex with label 1, the maximum click will be the union of the clicks calculated for the descendants of the vertex, and the size of this click is equal to the sum of the click dimensions. Thus, alternately taking the maximum size and summing the values ​​for each vertex of the tree, we calculate the maximum size of the click, and alternately choosing the maximum click and combining, we construct the maximum click itself. A similar bottom-up passage approach allows us to obtain the maximum independent set, chromatic number, maximum clique coverage, and the existence of the Hamiltonian path [en] in linear time. You can also use codelines to determine in linear time whether two kographs are isomorphic.

If H is a generated subgraph of a kograf G , then H itself is a kograf. The Koderevo for H can be obtained by removing a part of the leaves from the Kodereva for G followed by the merging of vertices with a single descendant. It follows from Kruskal’s trees theorem that the relation to be generated by a subgraph is a good quasi-order on cographs (Damaschke 1990) . So, if a family of kografs (such as planar kografs) is closed with respect to the operation of constructing a generated subgraph, then it has a finite number of forbidden generated subgraphs [en] . From the point of view of computations, this means that checking whether a graph belongs to such a family can be performed in linear time if you use a bottom-up pass through the coder of the given graph.

References [edit]

• Prosenjit Bose, Jonathan Buss, Anna Lubiw Pattern matching for permutations // Information Processing Letters . - T. 65. - p. 277–283. - DOI: 10.1016 / S0020-0190 (97) 00209-3.
• Andreas Brandstädt, Van Bang Le, Jeremy P. Spinrad Graph Classes: A Survey. - SIAM Monographs on Discrete Mathematics and Applications, 1999. - ISBN 978-0-89871-432-6 ..
• M. Burlet, JP Uhry Topics on Perfect Graphs. - 1984. - T. 21. - p. 253–277 ..
• DG Corneil, H. Lerchs, L. Stewart Burlingham Complement reducible graphs // Discrete Applied Mathematics . - 1981. - V. 3. - T. 3. - P. 163–174. - DOI: 10.1016 / 0166-218X (81) 90013-5.
• DG Corneil, Y. Perl, LK Stewart A linear recognition algorithm for cographs // SIAM Journal on Computing . - 1985. - V. 4. - T. 14. - p. 926–934. —DOI: ​​10.1137 / 0214065.
• B. Courcelle, S. Olariu ; - 2000. - V. 1–3. - T. 101. - p. 77–144. - DOI: 10.1016 / S0166-218X (99) 00184-5.
• Peter Damaschke Induced subgraphs and well-quasi-ordering // Journal of Graph Theory . - 1990. - V. 4. - T. 14. - P. 427–435. - DOI: 10.1002 / jgt.3190140406.
• Emeric Gioan, Christophe Paul Split decomposition and graph-labelled trees: - 2008 ..
• Michel Habib, Christophe Paul A, for Discrete Applied Mathematics . - 2005. - V. 2. - T. 145. - P. 183–197. —DOI: ​​10.1016 / j.dam.2004.01.011.
• HA Jung On a class of poses and the corresponding comparability graphs // Journal of Combinatorial Theory, Series B. - 1978. - V. 2. - T. 24. - p. 125–133. —DOI: ​​10.1016 / 0095-8956 (78) 90013-8.
• H. Lerchs On cliques and kernels. - 1971 ..
• D. Seinsche on the property of the class of colorable graphs // Journal of Combinatorial Theory, Series B. - 1974. - V. 2. - T. 16. - p. 191–193. - DOI: 10.1016 / 0095-8956 (74) 90063-X.
• DP Sumner Dacey graphs // J. Austral. Math Soc. . - 1974. - V. 04. - T. 18. - P. 492–502. - DOI: 10.1017 / S1446788700029232.

External links [edit]