Lecture
| Signs of | 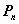 |
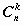 |
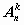 |
| The order of the elements | + | - | + |
| The composition of the elements | - | + | + |
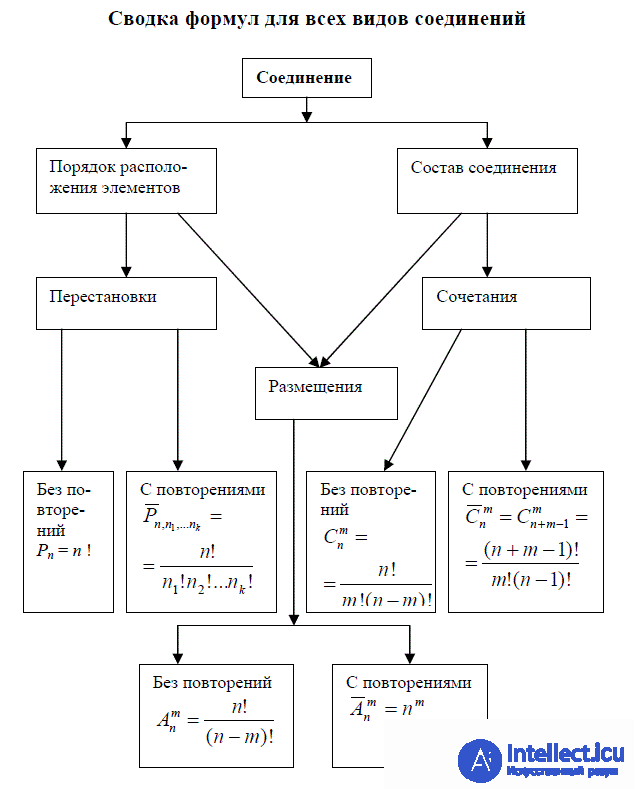

6 permutations of 3 balls
In combinatorics, transposition is an ordered set of numbers. 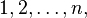 usually interpreted as a bijection on a set
usually interpreted as a bijection on a set 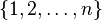 The i- th element from the set corresponds to i . The number n is here called the permutation order . As a synonym for the word "permutation" in this sense, some authors use the word arrangement .
The i- th element from the set corresponds to i . The number n is here called the permutation order . As a synonym for the word "permutation" in this sense, some authors use the word arrangement .
In group theory, a permutation of an arbitrary set means a bijection of this set onto itself. As a synonym for the word "permutation" in this sense, some authors use the word substitution . (Other authors refer to substitution as a visual way of recording a permutation.)
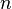 equal to the number of allocations from n to n , that is, factorial: [1] [2] [3] [4]
equal to the number of allocations from n to n , that is, factorial: [1] [2] [3] [4]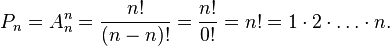
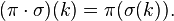 Regarding this operation, the set of permutations of order n forms a group, which is called symmetric and is usually denoted
Regarding this operation, the set of permutations of order n forms a group, which is called symmetric and is usually denoted 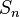 .
.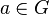 matches the permutation
matches the permutation 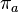 given by identity
given by identity 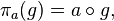 where g is an arbitrary element of the group G , and
where g is an arbitrary element of the group G , and  - group operation.
- group operation.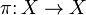 Is a subset of the set
Is a subset of the set 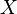 defined as
defined as 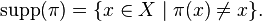
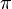 is any fixed point display
is any fixed point display 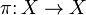 that is, the element of the set
that is, the element of the set 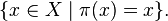 The set of all fixed permutation points
The set of all fixed permutation points 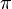 is an addition to its carrier in
is an addition to its carrier in 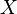 .
.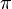 order n is called every pair of indices
order n is called every pair of indices 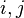 such that
such that 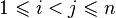 and
and 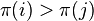 . The parity of the number of inversions in a permutation determines the parity of the permutation .
. The parity of the number of inversions in a permutation determines the parity of the permutation .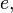 which is each item
which is each item 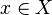 displays in itself:
displays in itself: 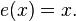
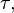 which is the reverse of itself, that is
which is the reverse of itself, that is 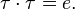
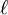 called such a substitution
called such a substitution 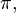 which is identical on the whole set
which is identical on the whole set 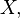 except a subset
except a subset 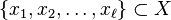 and
and 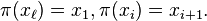 Denoted by
Denoted by 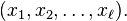 . The number of permutations containing k cycles is Stirling numbers of the first kind.
. The number of permutations containing k cycles is Stirling numbers of the first kind.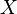 which swaps two elements. Transposition is a cycle of length 2.
which swaps two elements. Transposition is a cycle of length 2.Permutation 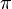 sets
sets 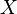 can be written as a substitution , for example:
can be written as a substitution , for example:
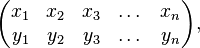
Where 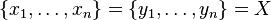 and
and 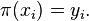
Any permutation 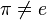 can be decomposed into a product (composition) of disjoint length cycles
can be decomposed into a product (composition) of disjoint length cycles 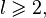 and uniquely up to the order of the cycles in the product. For example:
and uniquely up to the order of the cycles in the product. For example:
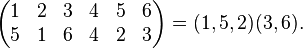
Any cycle can be decomposed into a product of (not necessarily disjoint) transpositions. For arbitrary length cycle  decomposition can be written like this:
decomposition can be written like this: 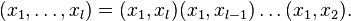 Loops of length 1 act as the identity permutation and can also be easily decomposed, since the square of any transposition is the identity permutation:
Loops of length 1 act as the identity permutation and can also be easily decomposed, since the square of any transposition is the identity permutation: 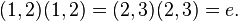 Such a decomposition of cycles into a product of transpositions will not be the only one:
Such a decomposition of cycles into a product of transpositions will not be the only one: 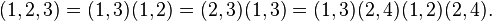
Thus, any permutation can be decomposed into a product of transpositions. Although this decomposition will not be unique, but the parity of the number of transpositions included in the decomposition is preserved. Let the permutation 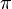 laid out in the product
laid out in the product 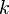 transpositions, then the permutation sign (otherwise: the permutation parity or permutation signature )
transpositions, then the permutation sign (otherwise: the permutation parity or permutation signature ) 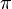 call the number
call the number 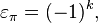 wherein
wherein 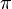 called an even permutation if
called an even permutation if 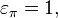 and an odd permutation if
and an odd permutation if 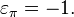
Permutation Sign 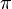 can also be determined through the number of inversions
can also be determined through the number of inversions 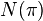 in this permutation:
in this permutation: 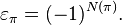
Comment. There are two conventions for multiplying permutations and cycles:
one) 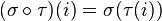 .
.
For example: 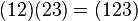 .
.
2) 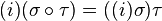 .
.
For example: 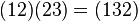 .
.
Consider n elements of m different types, and in each type all elements are the same. Then the permutations of all these elements up to the order of the sequence of similar elements are called permutations with repetition . If k i is the number of elements of the i -th type, then 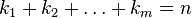 and the number of various permutations with repetitions is equal to the multinomial coefficient
and the number of various permutations with repetitions is equal to the multinomial coefficient 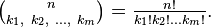
Main article: Generalized layout
Random permutation is called a random vector. 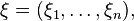 all elements of which take natural values from 1 to
all elements of which take natural values from 1 to 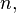 and the probability of coincidence of any two elements is 0.
and the probability of coincidence of any two elements is 0.
An independent random permutation is such a random permutation. 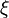 , for which
, for which
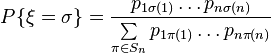
for some 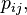 such that
such that
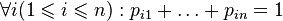
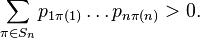
If at the same time 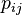 do not depend on
do not depend on 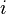 then the permutation
then the permutation 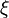 called equally distributed . If there is no dependence on
called equally distributed . If there is no dependence on 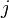 , i.e
, i.e 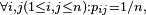 that
that 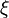 called homogeneous .
called homogeneous .
In combinatorics, an arrangement (from n to k ) is an ordered set of k different elements from some set of different n elements.
Example 1: 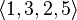 - This is a 4-element placement from a 6-element set.
- This is a 4-element placement from a 6-element set. 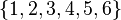 .
.
Example 2: some placements of the elements of a set 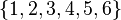 on 2:
on 2: 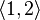
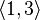
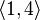
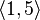 ...
... 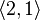
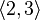
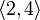 ...
... 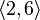 ...
...
Unlike combinations, placements take into account the order of the objects. So, for example, sets 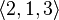 and
and 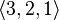 are different though they consist of the same elements.
are different though they consist of the same elements. 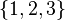 (i.e., match as combinations).
(i.e., match as combinations).
The number of allocations of n for k , denoted by 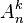 , is equal to decreasing factorial:
, is equal to decreasing factorial:
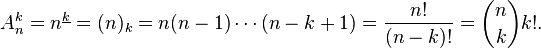
The last expression has a natural combinatorial interpretation: each placement from n to k uniquely corresponds to some combination of n to k and some rearrangement of the elements of this combination; the number of combinations of n in k is equal to the binomial coefficient 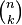 , while permutations on k elements are exactly k! pieces
, while permutations on k elements are exactly k! pieces
For k = n, the number of placements is equal to the number of permutations of order n :
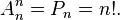
Posting or returning is the placement of “items” under the assumption that each “item” can participate in the placement several times.
By the multiplication rule, the number of arrangements with repetitions of n by k , denoted by 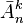 , equals:
, equals:
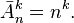
For example, the number of variants of a 3-digit code, in which each character is a digit from 0 to 9 and can be repeated, is:
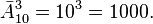
Another example: placements with repetitions of 4 elements a, b, c, d with 2 are 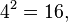 these accommodations are as follows:
these accommodations are as follows:
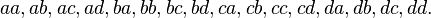
In combinatorics, the combination of 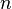 by
by 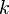 called a set
called a set 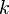 elements selected from this set containing
elements selected from this set containing 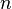 various items. Sets that differ only in the order of the elements (but not the composition) are considered to be the same, this combination differs from placements.
various items. Sets that differ only in the order of the elements (but not the composition) are considered to be the same, this combination differs from placements.
So, for example, sets (3-element combinations, subsets, 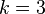 ) {2, 1, 3} and {3, 2, 1} of the 6-element set {1, 2, 3, 4, 5, 6} (
) {2, 1, 3} and {3, 2, 1} of the 6-element set {1, 2, 3, 4, 5, 6} ( 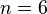 ) are the same (while the placement would be different) and consist of the same elements {1,2,3}.
) are the same (while the placement would be different) and consist of the same elements {1,2,3}.
In general, a number indicating how many ways you can choose 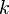 elements from the set containing
elements from the set containing 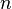 different elements standing at the intersection
different elements standing at the intersection 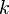 th diagonal and
th diagonal and 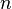 Pascal's triangle line. [one]
Pascal's triangle line. [one]
Main article: Binomial coefficient
Combination of 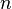 by
by 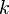 equal to the binomial coefficient
equal to the binomial coefficient
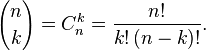
With fixed  generating function of a sequence of numbers of combinations
generating function of a sequence of numbers of combinations  ,
, 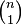 ,
, 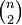 , … is an:
, … is an:
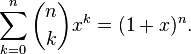
The two-dimensional generating function of the numbers of combinations is
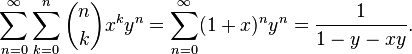
Combination with repetitions are called sets, in which each element can participate several times.
The number of combinations with repetitions from 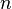 by
by 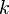 equal to the binomial coefficient
equal to the binomial coefficient
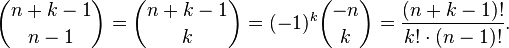
Evidence
Let there be 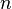 object types, and objects of the same type are indistinguishable. Suppose there is an unlimited (or large enough, in any case, no less than
object types, and objects of the same type are indistinguishable. Suppose there is an unlimited (or large enough, in any case, no less than 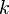 ) the number of objects of each type. From this range, choose
) the number of objects of each type. From this range, choose 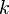 objects; The sample can contain objects of the same type, the order of selection does not matter. Denote by
objects; The sample can contain objects of the same type, the order of selection does not matter. Denote by 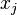 number of selected objects of
number of selected objects of 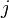 type i,
type i,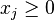 ,
, 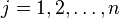 . Then
. Then 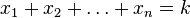 .But the number of solutions of this equation is easily calculated with the help of “balls and partitions”: each solution corresponds to the arrangement of
.But the number of solutions of this equation is easily calculated with the help of “balls and partitions”: each solution corresponds to the arrangement of 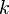 balls and
balls and 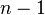 partitions in a series so that exactly balls are located between the
partitions in a series so that exactly balls are located between the 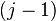 -th and
-th and 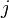 -th partitions
-th partitions 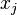 . But such arrangements are exactly
. But such arrangements are exactly 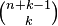 what was required to prove. ■
what was required to prove. ■
With a fixed 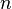 generating function of numbers of combinations with repetitions from
generating function of numbers of combinations with repetitions from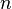 by
by 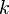 is an:
is an:
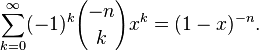
The two-dimensional generating function of numbers of combinations with repetitions is:
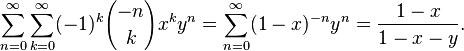
еще систематизировать информацию можно в этой статье
https://intellect.icu/formuly-dlya-vsekh-vidov-soedinenij-v-kombinatorike-perestanovki-i-razmeshheniya-s-povtoreniyami-i-bez-povtorenij-s-primerami-4270
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.