Lecture


In mathematics, the four-color theorem states that any map located on a sphere can be colored with four colors so that any two regions that have a common part of the boundary are colored in different colors. In this case, it is assumed that each region is simply connected, and a common part of the border is a part of a line, that is, the joints of several areas at one point are not considered to be a common border. This theorem was formulated by Francis Guthrie ( English ) in 1852, but it was not possible to prove it for a long time. During this time, there have been many attempts at both proof and refutation, and this task was called the problem of four colors .
The task of coloring a map on a plane is equivalent to a problem on a sphere.
For simple cards, three colors are enough, and the fourth color begins to be required, for example, when there is one area surrounded by an odd number of others that are in contact with each other, forming a cycle. The five-color theorem, which asserts that five colors are sufficient, had a short simple proof and was proved at the end of the 19th century, but the proof of the theorem for the case of four colors was faced with considerable difficulties.
The four-color theorem was proved in 1976 by Kenneth Appel ( Eng. ) And Wolfgang Hacken ( Eng. ) From the University of Illinois. It was the first major mathematical theorem, proved by computer. The first step of the proof was the demonstration that there is a certain set of 1936 maps, none of which can contain a smaller map that would disprove the theorem. Appel and Hacken used a special computer program to prove this property for each of the 1936 maps. The proof of this fact took hundreds of pages. After that, Appel and Haken came to the conclusion that the smallest counterexample to the theorem does not exist, because otherwise it should contain, although it does not contain, any of these 1936 maps. This contradiction suggests that there is no counterexample at all. Initially, the proof was not accepted by all mathematicians, since it could not be checked manually. Later it gained wider recognition, although some had doubts for a long time.
To dispel the remaining doubts, in 1997, Robertson, Sanders, Seymour, and Thomas published simpler proof using similar ideas, but still done with a computer. In addition, in 2005, the proof was made by Georges Gontir using specialized software (Coqv7.3.1) [1] .
In graph theory, the statement of the four-color theorem has the following formulations:
The most famous evidence attempts:
Similar problems for other surfaces (torus, Klein bottle, etc.) were much simpler. For all closed surfaces, except for the sphere (and equivalent to the plane and cylinder) and the Klein bottle, the required number of colors can be calculated using the Eulerian characteristic  according to the formula proposed in 1890 by Percy John Heawood [5] and finally proved during 1952-1968 by a group of mathematicians with the greatest contribution of Gerhard Ringel and JTW Youngs [6] [7]
according to the formula proposed in 1890 by Percy John Heawood [5] and finally proved during 1952-1968 by a group of mathematicians with the greatest contribution of Gerhard Ringel and JTW Youngs [6] [7]
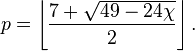
For a Klein bottle, the number is 6 (and not 7, as according to the formula) - this was shown by P. Franklin in 1934, [8] and for the sphere - 4.
For one-sided surfaces [7]
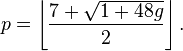 .
. In the higher dimensions, a reasonable generalization of the problem does not exist, since it is easy to come up with a three-dimensional map with an arbitrary number of areas that all touch each other.
Stephen Barr proposed a two-player puzzle game called Four Colors. According to Martin Gardner - “I don’t know a better way to understand the difficulties that are encountered in solving the problem of four colors than just playing this interesting game” [9] .
Four colored pencils are needed for this game. The first player starts the game by drawing an arbitrary empty area. The second player paints it in any of the four colors and in turn draws his empty area. The first player paints over the area of the second player and adds a new area, and so on - each player paints the opponent's area and adds his own. In this area, having a common border, should be painted in different colors. The one who is forced to take the fifth paint at his own turn loses.
It is worth noting that in this game, the loss of one of the players is not at all evidence of the theorem's infidelity (four colors were not enough!). But only an illustration of the fact that the conditions of the game and the theorems are quite different. To verify the correctness of the theorem for the map obtained in the game, you need to check the connectivity of the drawn areas and, removing colors from it, find out if you can do with only four colors to paint the resulting map (the theorem states that you can).
There are also the following variations of the game:
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.