Lecture
The Euler path (Euler chain) in a graph is the path (chain) passing along all the arcs (edges) of a graph and, moreover, only once. (cf. Hamiltonian way)
Euler cycle is a cycle of a graph passing through each edge (arc) of a graph exactly once.
Euler graph is a graph containing an Euler cycle.
Half-count graph is a graph containing an Eulerian path (chain).

Count Konigsberg bridges. This graph is not Eulerian, so there is no solution.

Each vertex of this graph has an even degree, so this graph is Eulerian. Traversing the edges in alphabetical order gives the Eulerian cycle.
Definition 3
The chain containing all the edges of the graph is called Euler.
Definition 4
A graph possessing an Euler chain is called quasieller.
Theorem 5
A graph is quasieller if it has at most two vertices of odd degree.
| Definition 1 |
|
A cycle is called Eulerian if it contains all the edges of the graph. A chain is called Euler if it contains all the edges of the graph. |
| Definition 2 |
|
A graph is called Eulerian if there is an Euler cycle in it.
Example
The “Sabers of Mahomet” graph is Eulerian, since it contains the Eulerian cycle 123475287651.
|
The Euler cycle / path exists only in connected graphs or in graphs, which, after removing all single vertices, will become connected.
According to the theorem proved by Euler, in a graph without single vertices of an Eulerian cycle there exists if and only if there is no graph of a graph and there are no vertices of odd degree in it.
An Euler chain in a graph exists if and only if the graph is connected and contains at most two vertices of odd degree. [1] [2] In view of the handshake lemma, the number of vertices with an odd degree must be even. So Euler path exists only when this number is zero or two. And when it is zero, the Eulerian path degenerates into an Eulerian cycle.
Oriented graph 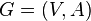 contains an Eulerian cycle if and only if it is strongly connected and for each vertex of the graph its half degree of approach is equal to its half degree of outcome, that is, the same number of edges enter the top as there are from it:
contains an Eulerian cycle if and only if it is strongly connected and for each vertex of the graph its half degree of approach is equal to its half degree of outcome, that is, the same number of edges enter the top as there are from it: 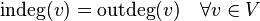 .
.
Oriented graph 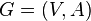 contains an Eulerian path if and only if it is strongly connected and there exist two vertices
contains an Eulerian path if and only if it is strongly connected and there exist two vertices 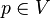 and
and 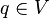 (the initial and final vertices of the path, respectively) such that their half-degrees of approach
(the initial and final vertices of the path, respectively) such that their half-degrees of approach 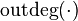 and half-degrees of outcome
and half-degrees of outcome 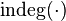 bound by equalities
bound by equalities 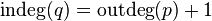 and
and 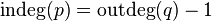 , and all other vertices have the same half degree of outcome and approach:
, and all other vertices have the same half degree of outcome and approach: 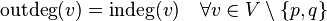 .
.
You can always reduce the task of finding the Euler path to the task of finding the Euler cycle. Indeed, suppose that the Eulerian cycle does not exist, and the Euler path exists. Then the graph will have exactly 2 vertices of odd degree. We connect these vertices with an edge, and we obtain a graph in which all the vertices are of even degree, and the Eulerian cycle exists in it. We find a cycle in this Euler graph (using the algorithm described below), and then remove the nonexistent edge from the answer.
This is an elegant but inefficient algorithm, proposed by Fleury in 1883.
Let the graph be given 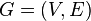 . Starting at some vertex
. Starting at some vertex 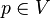 and each time we cross out the passed edge. We do not pass along the edge, if the removal of this edge results in splitting the graph into two connected components (not counting the isolated vertices), i.e. it is necessary to check whether the edge is a bridge or not.
and each time we cross out the passed edge. We do not pass along the edge, if the removal of this edge results in splitting the graph into two connected components (not counting the isolated vertices), i.e. it is necessary to check whether the edge is a bridge or not.
The algorithm can be extended to digraphs.
We will consider the most general case - the case of an oriented multigraph, possibly with loops. We also assume that the Euler cycle in the graph exists (and consists of at least one vertex). To search for the Eulerian cycle, we use the fact that the Eulerian cycle is the union of all simple cycles of the graph. Therefore, our task is to efficiently find all the cycles and effectively combine them into one.
This can be implemented, for example, recursively:
procedure find_all_cycles (v)
var cycles array
1. while there is a loop going through v, we find it
add all vertices of the found loop to the cycles array (preserving the traversal order)
delete cycle from graph
2. go through the elements of the array of cycles
each cycles [i] element is added to the response
from each element we recursively call ourselves: find_all_cycles (cycles [i])
It is enough to call this procedure from any non-single vertex of the graph, and it will find all the cycles in the graph, remove them from the graph and combine them into one Eulerian cycle.
To search for a loop in step 1, use depth search.
The complexity of the algorithm obtained is O (M), that is, linear with respect to the number of edges M in this graph.
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.