Lecture
| Wheel graph examples | |
 |
|
| Tops |
n |
|---|---|
| Rib |
2 ( n - 1) |
| Diameter |
2 when n> 4 |
| Girth |
3 |
| Chromatic number |
3 for odd n , 4 for even n |
| Properties |
Hamiltonian |
| Designation |
W n |
|
|
|
In graph theory, the wheel W n is a graph with n vertices (n ≥ 4), formed by connecting a single vertex with all vertices of the ( n -1) -cycle. The numerical designation of wheels in the literature is not well established - some authors use n to denote the length of the cycle, so their W n means the graph W n + 1 by definition above. [1] The wheel can also be defined as a 1-skeleton [en] ( n -1) -pound pyramid.
Let the set of vertices {1,2,3, ..., v} be given. The set of edges of the wheel graph can be represented as a set {{1,2}, {1,3}, ..., {1, v}, {2,3}, {3,4}, ..., {v -1, v}, {v, 2}}. [2]
The wheels are planar graphs, and therefore have a single investment in the plane. Any wheel is a graph Khalina. They are self-dual — the dual graph of any wheel is isomorphic to the wheel itself. Any maximum planar graph other than K 4 = W 4 contains either W 5 or W 6 as a subgraph.
The wheel always has a Hamiltonian cycle and the number of cycles in W n is equal to 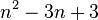 (sequence A002061 in OEIS).
(sequence A002061 in OEIS).
 7 cycles in the wheel W 4 . |
For odd n values, W n is a perfect graph with a chromatic number of 3 — the cycle vertices can be colored in two colors, and the central vertex will have a third color. For even n W n, the wheel has a chromatic number of 4 and (for n ≥ 6) it will not be a perfect graph. W 7 is the only wheel that is a graph of unit distances on the Euclidean plane. [3]
Chromatic polynomial wheel W n is equal to
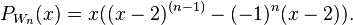
In the theory of matroids there are two especially important types of matroids - wheels and vortices , and both types are derived from wheel graphs. The matroid of the k- wheel is a graph matroid [en] of the wheel W k + 1 , and the matroid of the k- vortex is obtained from the matroid of the k- wheel by declaring an external cycle (rim) with the same independent set as its host trees.
The W 6 wheel gives a counterexample to Paul Erdös hypothesis in Ramsey theory — he suggested that a complete graph has the smallest Ramsey number among all graphs with the same chromatic number. However, Faudry and McKay (Faudree, McKay, 1993) showed that for W 6 the number of Ramsey is 17, while for the full graph K 4 with the same chromatic number Ramsey number is 18. [4] Thus, for any graph G with 17 vertices either G itself or its complement contains W 6 as a subgraph, while neither Paley graph with 17 vertices nor its complement contains K 4 .
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.