Lecture
Set is one of the key concepts of mathematics, in particular, set theory and logic.
The concept of a set is usually taken as one of the original (axiomatic) concepts, that is, irreducible to other concepts, and therefore not having a definition; descriptive formulations are used to explain it, characterizing the set as a set of different elements, conceivable as a whole [1] [2] . Indirect definition is also possible through axioms of set theory. A set can be empty and non-empty, ordered and unordered, finite and infinite, an infinite set can be countable or uncountable. Moreover, in both naive and axiomatic set theories, any object is usually considered a set.
The foundations of the theory of finite and infinite sets were laid by Bernard Bolzano, who formulated some of its principles.
From 1872 to 1897 (mainly in 1872–1884), Georg Cantor published a series of papers in which the main sections of set theory were systematically described, including the theory of point sets and the theory of transfinite numbers (cardinal and ordinal). In these works, he not only introduced the basic concepts of set theory, but also enriched mathematics with new type of reasoning, which he applied to prove theorems of set theory, in particular, for the first time to infinite sets. Therefore, it is generally accepted that Georg Cantor created set theory. In particular, he defined the set as “a single name for the totality of all objects with this property”. These objects are called elements of the set. Many objects with property 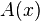 outlined
outlined 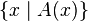 . If some set
. If some set 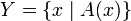 then
then 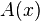 called the characteristic property of the set
called the characteristic property of the set 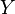 .
.
This concept led to paradoxes, in particular, to the Russell paradox.
Since set theory is actually used as the basis and language of all modern mathematical theories in 1908, set theory was axiomatized independently by Bertrand Russell and Ernst Zermelo. In the future, many researchers have revised and modified both systems, mostly retaining their character. Until now, they are still known as the Russell Type Theory and Zermelo Set Theory. Subsequently, the theory of sets of Kantor was called the naive theory of sets, and the newly constructed theory - the axiomatic theory of sets.
In the practice that has developed since the middle of the XX century, the set is defined as a model that satisfies the ZFC axioms (Zermelo – Fraenkel axioms with the axiom of choice). With this approach, in some mathematical theories arise sets of objects that are not sets. Such aggregates are called classes (of various orders).
The objects that make up a set are called the elements of a set or points of a set. Sets are most often denoted by capital letters of the Latin alphabet, its elements - lowercase. If a 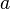 - set element
- set element 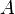 then write down
then write down 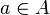 ("
(" 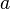 belongs
belongs 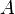 "). If a
"). If a 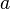 not an element of the set
not an element of the set 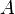 then write down
then write down 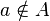 ("
(" 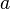 not belong
not belong 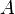 "). Unlike a multiset, each element of a set is unique, and there cannot be two identical elements in a set. In other words, adding to the set of elements identical to those already belonging to the set does not change it:
"). Unlike a multiset, each element of a set is unique, and there cannot be two identical elements in a set. In other words, adding to the set of elements identical to those already belonging to the set does not change it:
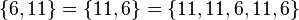 .
.
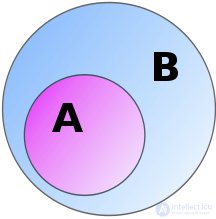
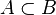
Two sets 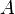 and
and 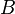 may enter into different relationships with each other.
may enter into different relationships with each other.
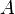 included in
included in 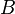 if each element of the set
if each element of the set 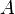 also belongs to the set
also belongs to the set 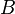 :
:
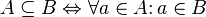
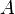 includes
includes 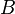 , if a
, if a 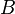 included in
included in 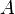 :
:
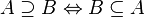
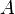 equally
equally 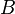 , if a
, if a 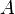 and
and 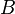 included in each other:
included in each other:
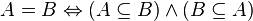
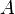 strictly included in
strictly included in 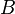 , if a
, if a 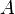 included in
included in 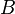 but not equal to him:
but not equal to him:
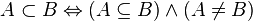
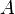 strictly includes
strictly includes 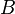 , if a
, if a 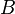 strictly included in
strictly included in 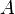 :
:

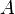 and
and 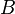 do not intersect if they have no common elements:
do not intersect if they have no common elements:
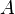 and
and 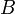 do not intersect
do not intersect 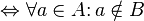
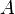 and
and 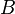 are in general position if there exists an element belonging exclusively to the set
are in general position if there exists an element belonging exclusively to the set 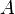 , an element belonging exclusively to the set
, an element belonging exclusively to the set 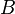 , as well as an element belonging to both sets:
, as well as an element belonging to both sets:
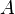 and
and 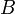 are in general position
are in general position 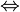
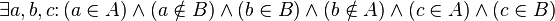
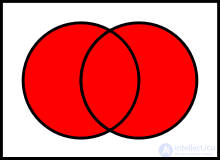
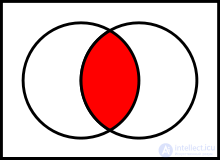
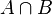
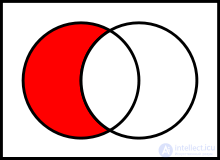
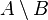
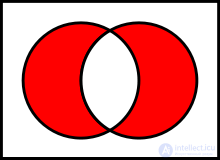
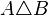
Basic binary operations defined on sets:
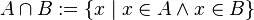 .
.
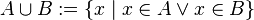 .
.
If sets 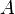 and
and 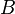 don't intersect then
don't intersect then 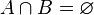 . Their association also means:
. Their association also means: 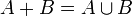 .
.
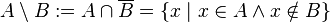 .
.
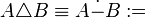
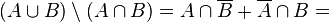
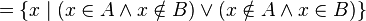 .
.
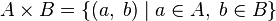 .
.
To explain the meaning of operations, Venn diagrams are often used, which present the results of operations on geometric shapes as sets of points.
Any system of sets that is closed with respect to the operations of union and intersection forms a distributive lattice with respect to the union and intersection.
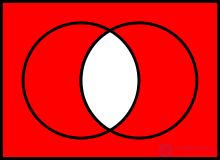
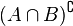
Addition is determined as follows:
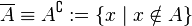 .
.
The addition operation implies some fixed universe (the universal set  which contains
which contains 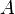 ), and it comes down to the difference of sets with this universe:
), and it comes down to the difference of sets with this universe:
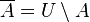 .
.
The system of sets with a fixed universe, closed with respect to the operations of union, the intersection with the addition thus introduced forms a Boolean algebra.
Boolean - the set of all subsets:
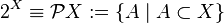 .
.
Designation 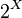 derives from the power property of the set of all subsets of a finite set:
derives from the power property of the set of all subsets of a finite set:
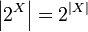 .
.
Boolean 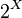 generates a system of sets with a fixed universe
generates a system of sets with a fixed universe 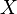 , closed with respect to the operations of union and intersection, that is, forms a Boolean algebra.
, closed with respect to the operations of union and intersection, that is, forms a Boolean algebra.
First, unary operations (additions) are performed, then intersections, then unions and differences that have the same priority. The sequence of operations can be changed by brackets.
The power of a set is a characteristic of a set that generalizes the concept of the number of elements for a finite set in such a way that sets between which it is possible to establish a bijection are equal. Denoted by 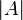 or
or 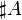 . The power of an empty set is zero; for finite sets, the power coincides with the number of elements; for infinite sets, special cardinal numbers are introduced that correspond with each other according to the inclusion principle (if
. The power of an empty set is zero; for finite sets, the power coincides with the number of elements; for infinite sets, special cardinal numbers are introduced that correspond with each other according to the inclusion principle (if 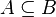 then
then 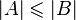 ) and the propagation of the power property of a boolean of a finite set:
) and the propagation of the power property of a boolean of a finite set: 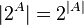 in the case of infinite sets (the very notation
in the case of infinite sets (the very notation 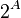 motivated by this property).
motivated by this property).
The smallest infinite power is indicated by 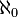 This is the power of a countable set. The power of the continuum, a bijective boolean of a countable set, is denoted by
This is the power of a countable set. The power of the continuum, a bijective boolean of a countable set, is denoted by  or
or 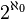 . Continuum hypothesis is the assumption that there are no intermediate powers between the calculated power and the power of the continuum.
. Continuum hypothesis is the assumption that there are no intermediate powers between the calculated power and the power of the continuum.
By “set” we mean connecting into a certain whole M certain well-distinguishable objects m of our contemplation or our thinking (which will be called the “elements” of the set M).
Original Text (German)Unter einers
- Russian translation - Kantor G. Trudy on set theory. - M .: Science, 1985. - p. 173 .. German original - Georg Cantor. Beiträge zur Begründung der transfiniten Mengenlehre (German) // Mathematische Annalen . - 1895. - V. 46. - p. 481.
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.