Lecture
In graph theory, the edge graph L ( G ) of a non-oriented graph G is the graph L ( G ) representing the neighborhood of the edges of the graph G.
The concept of the edge graph for a given graph is so natural that it was independently introduced by many authors. Of course, each of them gave its name: Ore [1] called this graph "adjacent graph", Sabidussi [2] - "derivative graph", Beineke [3] - "derivative graph", Seshu and Reed [4] - "edge - vertex-dual ", Castellin [5] -" covering graph ", Menon [6] -" connected "(" conjugate ") [7] [8] [9] .
One of the earliest and most important theorems on edge graphs belongs to Whitney, who proved that, with one exception, the structure of graph G is completely determined by the edge graph. In other words, with one exception, the entire graph can be recovered from the edge graph.
Let a graph G be given, then its edge graph L ( G ) is a graph such that
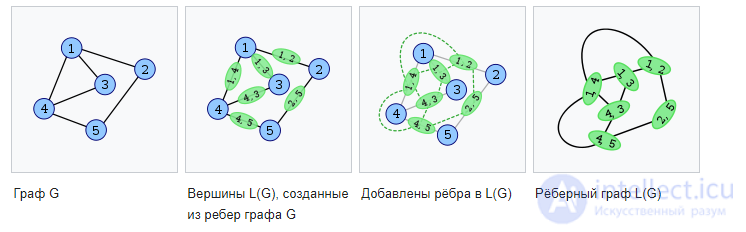
The next figure shows a graph (on the left, with blue vertices) and its edge graph (on the right, with green vertices). Each vertex of the edge graph is labeled with a pair of vertex numbers of the corresponding edge in the original graph. For example, the green vertex on the right with the label 1.3 corresponds to the edge on the left between blue vertices 1 and 3. The green vertex 1.3 is adjacent to three other green vertices: 1.4, 1.2 (corresponding to edges with common vertex 1 in the blue graph) and 4.3 (corresponding to edges with a common vertex 3 in a blue graph).
The edge graph of the complete graph K n is known as a chordal graph (or a triangulated graph ). An important theorem on chordal graphs is a theorem stating that a chordal graph is characterized by a spectrum [en] , with the exception of n = 8, when there are three other graphs with the same spectrum as that of L ( K 8 ). Exceptions are explained in graph switching.
The source of examples of edge graphs can be found in geometry - for graphs of simple polytopes. If we construct the edge graph for the tetrahedron graph, we get the octahedron graph. From the cube graph, we get a cuboctahedron graph. From the graph of the dodecahedron, we obtain the graph of an icosododecahedron, etc. .. Geometrically, the operation consists of cutting off all the vertices of the polyhedron by a plane intersecting all the edges associated with the vertex in their middle.
If the polyhedron is not simple (that is, it has more than three faces per vertex), the edge graph will not be flat.
Main article: Middle Count
The median graph is a variant of the edge graph for a flat graph. In a median graph, two vertices are adjacent if and only if the corresponding edges of the original graph are two consecutive edges of a certain area of a flat graph. For simple polygons, the middle graph and the edge graph are the same, but for complex polygons, the middle graph remains flat. Thus, the median graphs of the cube and octahedron are isomorphic to the graph of a cubooctahedron, and the median graphs of the twelve hexagon and the icosahedron are isomorphic to the graph of the icosododecahedron.
Properties of the graph G that depend only on the adjacency of edges can be translated into equivalent properties of the graph L ( G ), depending only on the adjacency of the vertices. For example, the matching in G is a set of arcs, none of which is adjacent to the other, and the corresponding set of vertices in L ( G ), none of which are adjacent to the other, that is, the Independent set of vertices [en] .
So,
Since the maximum matching can be found in polynomial time, the maximum independent set of the edge graph can be found in polynomial time despite the difficulty of finding such a set for more general families of graphs.
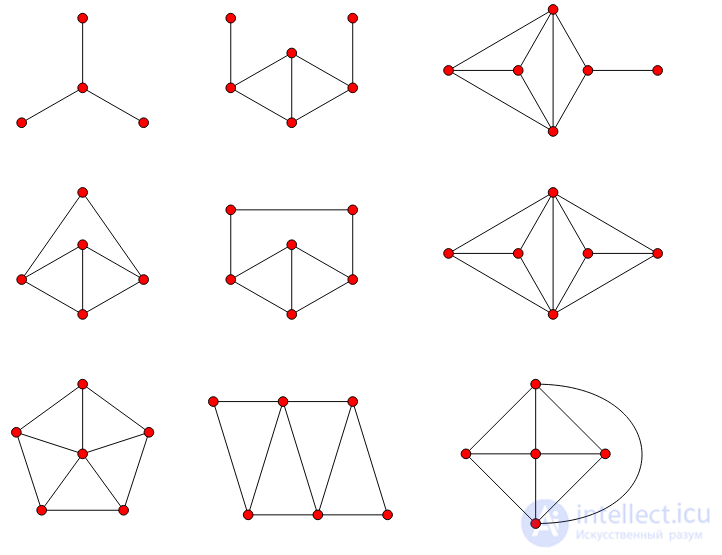
Nine minimal non-coastal graphs, among the characteristics of Beineke of forbidden subgraphs of edge graphs. A graph is edge-like if and only if it does not contain any of these nine graphs as a generated subgraph.
A graph G is the edge graph of some other graph if and only if it is possible to find a set in G that breaks the arcs of the graph G so that each vertex of G belongs to exactly two clicks. It may happen that to achieve this, you will need separate vertices to highlight in clicks. By the Whitney theorem [10] [11] , if G is not a triangle, there can be only one partition of this kind. If a partition exists, we can construct a graph for which G is a line graph by creating a vertex for each click and connecting the vertices obtained by an edge if the vertex belongs to both clicks. Thus, with the exception of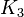 
and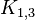 
if two edge graphs of connected graphs are isomorphic, then the graphs are also isomorphic. Rusopoulos (Roussopoulos) [12] used this observation as a basis for the time-linear algorithm for recognizing edge graphs and reconstructing their original graphs.
For example, such a characteristic can be used to show that the following graph is not edge:
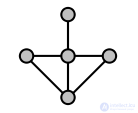
In this example, the edges going from the central vertex of the 4th degree up, left and right do not contain common clicks. So any division of the edges of a graph into clicks must contain at least one click for each of these three edges, and all three clicks intersect at the central vertex, which violates the condition that each vertex belong to exactly two clicks. Thus, the graph shown cannot be an edge graph.
Another characteristic of the graph was proved by Beineke [13] (and was mentioned without proof earlier by him [3] ). He showed that there are nine minimal graphs that are not edge, such that any graph that is not edge contains one of these nine graphs as a generated subgraph. Thus, a graph is edge if and only if no subset of vertices generates one of these nine. In the example above, the four upper peaks generate a claw (that is, a full bipartite graph K 1,3 ), shown in the upper left of the illustration of forbidden subgraphs. Thus, according to the Beineke characteristic, this graph cannot be edge. For graphs with a degree of vertices of at least 5, only six subgraphs in the left and right columns of the figure can be generated by the graph [14] . This result is similar to the result for the edge graphs of the hypergraph [en] . [15]
Ruidge and Wilf [16] reviewed the sequence of graphs
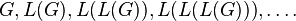
They showed that for a finite graph of a connected graph G , only four types of behavior of this sequence are possible:
If G is not connected, then this classification is applicable to every single connected component of the graph G.
Any edge graph does not contain claws.
The edge graph of a bichromatic graph is perfect (see the Koenig theorem [en] ). The edge graphs of bipartite graphs create one of the key blocks that is used to prove the perfect graph theorem. A special case is rook graphs, edge graphs of full dicotyledon graphs.
The concept of an edge graph for a graph G can be naturally extended to the case when G is a multigraph, although in this case, the Whitney uniqueness theorem becomes incorrect. For example, a full bipartite graph K 1, n has the same edge graph as the dipole graph [en] and the Shannonas multigraph with the same number of edges.
You can also generalize edge graphs for directed graphs. [17] . If G is a directed graph, then its oriented edge graph or a line digraph has one vertex for each arc of G. Two vertices corresponding to arcs from u to v and from w to x from graph G are connected by an arc from uv to wx in the edge digraph, when v = w . Thus, each arc in the edge digraph corresponds to a path of length 2 in the original graph. De Bruin graphs can be obtained by repeatedly constructing oriented edge graphs, starting with a complete digraph [18] .
Each vertex of degree k in the original graph G creates k (k-1) / 2 edges in the edge graph L ( G ). For many types of analysis, this means that the vertices of high degrees in G are represented more strongly in the line graph L ( G ). Imagine, for example, a random walk along the vertices of the original graph G. We pass along edge e with some probability f . On the other hand, the edge e corresponds to a single vertex, say v , in the edge graph L ( G ). If we now carry out the same type of random walk along the vertices of the edge graph, the frequency of visits v may turn out to be completely different from f . If our edge e in G was connected to vertices of degree O (k) , it will be passed in O (k 2 ) more often in the edge graph L ( G ). Thus, although the Whitney theorem [10] ensures that the edge graph almost always contains the coded topology of the graph G , this does not guarantee that these two graphs have simple dynamic connections. One of the solutions to this problem is to create a weighted edge graph, that is, a edge graph whose edges have weight. There are several natural ways to do this [19] . For example, if the edges d and e in the graph G are conjugate at the vertex v , which has degree k , then in the edge graph L ( G ), the edge connecting the two vertices d and e can be assigned a weight of 1 / (k-1) . In the same way, any edge of the graph G (unless it is connected to a vertex of degree '1') will have weight 2 in the edge graph L ( G ), which corresponds to the two ends of the edge in G.
The edges of a hypergraph can form any family of sets, so the line graph of a hypergraph is the same as the intersection graph of sets of a family.
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.