Lecture
The formula of inclusions-exceptions (or the principle of inclusions-exceptions ) is a combinatorial formula that allows you to determine the power of the union of a finite number of finite sets, which in the general case can intersect with each other. In probability theory, an analogue of the inclusion-exclusion principle is known as the Poincaré formula.
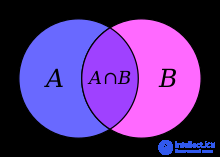
The case of two sets
For example, in the case of two sets 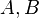 the formula of inclusions-exceptions is:
the formula of inclusions-exceptions is:
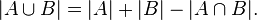
In total 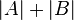 intersection elements
intersection elements 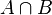 taken into account twice, and to compensate for this, we subtract
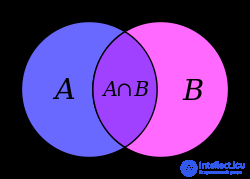
taken into account twice, and to compensate for this, we subtract 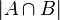 from the right side of the formula. The validity of this reasoning is visible from the Euler-Venn diagram for the two sets shown in the figure on the right.
from the right side of the formula. The validity of this reasoning is visible from the Euler-Venn diagram for the two sets shown in the figure on the right.
In the same way and in the case 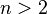 sets the process of finding the number of elements of the union
sets the process of finding the number of elements of the union 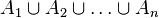 consists in including everything, then excluding the superfluous, then including the erroneously excluded, and so on, that is, in alternate inclusion and exclusion. Hence the name of the formula.
consists in including everything, then excluding the superfluous, then including the erroneously excluded, and so on, that is, in alternate inclusion and exclusion. Hence the name of the formula.
The formula of inclusions-exceptions can be formulated in different forms.
Let be 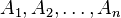 - finite sets. The formula of inclusions-exceptions states:
- finite sets. The formula of inclusions-exceptions states:
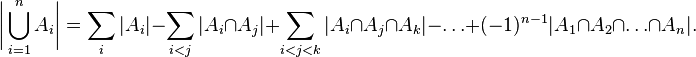
With 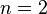 we obtain the formula for the two sets given above.
we obtain the formula for the two sets given above.
The principle of inclusions-exclusions is often given in the following alternative formulation [2]. Let given a finite set  . Then the formula is:
. Then the formula is:
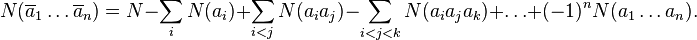
The formulation of the principle of inclusions-exceptions in terms of sets is equivalent to a formulation in terms of properties. Indeed, if the sets 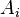 ), and the inclusion-exception formula can be rewritten as:
), and the inclusion-exception formula can be rewritten as:
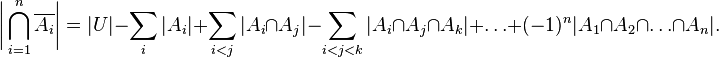
If now instead of "element 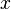 , Then we get the formulation of the principle of inclusions-exceptions in terms of properties, and vice versa.
, Then we get the formulation of the principle of inclusions-exceptions in terms of properties, and vice versa.
Denote by 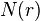 Then the formula of inclusions-exceptions can be rewritten in the following closed form ( English ) .
Then the formula of inclusions-exceptions can be rewritten in the following closed form ( English ) .
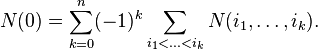
There are several proofs of the formula for inclusion inclusions.
Proof by induction
The formula for inclusions-exclusions can be proved by induction [1] [3].
With 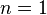 the inclusion-exclusion formula is trivial:
the inclusion-exclusion formula is trivial:
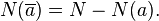
Let the formula be true for 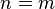 .
.
Let each element of the set 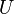 :
:
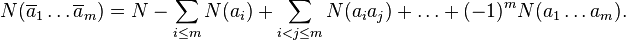
Now apply the formula for the properties 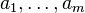 :
:
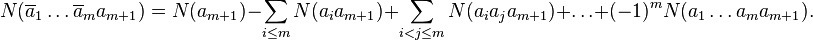
Finally, apply the formula for one property 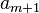 :
:
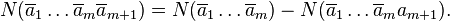
Combining the three formulas, we obtain the formula of inclusions-exceptions for 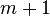 . Q.E.D. ■
. Q.E.D. ■
Combinatorial evidence
Consider an arbitrary element 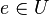 [2].
[2].
If the item  ).
).
Let element  in the right side is equal to
in the right side is equal to
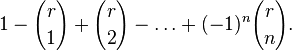
With 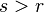 combination numbers are zero. The remaining sum due to the binomial theorem is equal to
combination numbers are zero. The remaining sum due to the binomial theorem is equal to
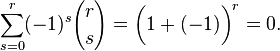
Thus, the right-hand part of the formula of inclusions-exclusions takes into account each element that does not have the specified properties exactly once, and each element that has at least one of the properties zero times. Therefore, it is equal to the number of elements that do not possess any of the properties 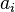 . Q.E.D. ■
. Q.E.D. ■
Proof through indicator functions
Let be 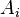 ).
).
Indicator function of their additions 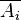 equals
equals
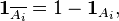
and the indicator function of the intersection of additions:
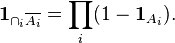
Opening the brackets in the right part and again using the fact that the indicator function of intersection of sets is equal to the product of their indicator functions, we get:
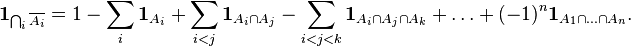
This ratio is one of the forms of the principle of inclusions-exceptions. It expresses a logical identity [1] and is true for arbitrary sets 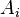 its power is equal to
its power is equal to
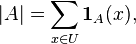
we obtain the formulation of the principle of inclusions-exceptions in terms of cardinalities of sets (or in terms of properties). ■
Riot problem
A classic example of the use of the inclusion-exclusion formula is the problem of unrest [2]. Required to find the number of permutations 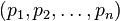 . Such permutations are called unrest.
. Such permutations are called unrest.
Let be 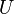 unrest:
unrest:
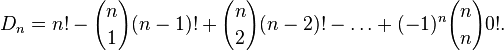
This ratio can be converted to the form
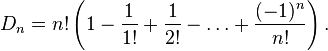
It is easy to see that the expression in brackets is a partial sum of a series 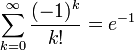 permutations:
permutations:
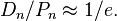
Another example of using the inclusion-exception formula is finding an explicit expression for the Euler function. 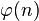 .
.
Let the canonical decomposition of a number 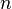 on prime factors looks like
on prime factors looks like
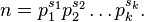
Number 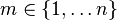 .
.
amount 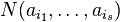 .
.
According to the formula of inclusions-exceptions we find
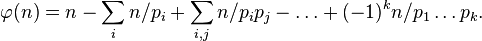
This formula is converted to the form:
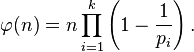
Let be  [five]
[five]
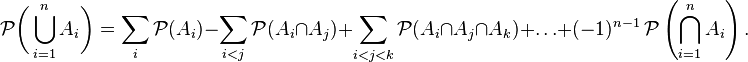
This formula expresses the principle of inclusions-exceptions for probabilities. It can be obtained from the principle of inclusions-exceptions in the form of indicator functions:
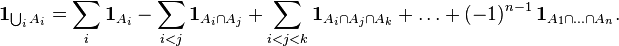
Let be 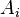 , we obtain the inclusion-exclusion formula for probabilities.
, we obtain the inclusion-exclusion formula for probabilities.
Let be 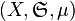 the inclusion-exception formula is:
the inclusion-exception formula is:
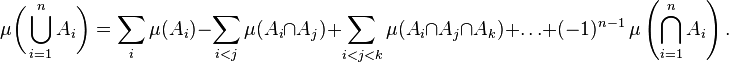
Obviously, the principle of inclusions-exceptions for probabilities and for the powers of finite sets are special cases of this formula. In the first case, the measure is, naturally, a probability measure in the corresponding probability space: 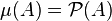 .
.
The principle of inclusions-exclusions for spaces with a measure can also be derived, as for the indicated special cases, from the identity for indicator functions:
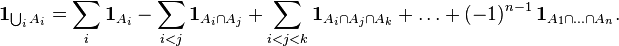
Let be 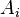 , and we obtain the formula of inclusions-exceptions for the measure.
, and we obtain the formula of inclusions-exceptions for the measure.
The formula of inclusions-exceptions can be considered as a special case of the identity of maxima and minima:
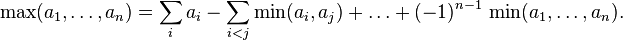
This relationship holds true for arbitrary numbers. 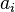 , then we obtain the ratio for the indicator functions of the sets:
, then we obtain the ratio for the indicator functions of the sets:
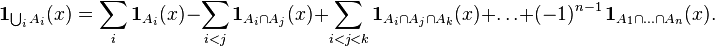
Let be 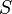 as follows:
as follows:
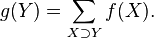
Then the following inversion formula takes place [6] [7]:
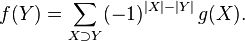
This statement is a special case of the general Mobius inversion formula for the incidence algebra ( English ) of the set 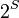 .
.
Let us show how the inclusion-exclusion principle for finite sets follows from this formula. Let a family of subsets be given 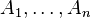 . Mathematically, it can be written like this:
. Mathematically, it can be written like this:
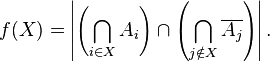
Then the function 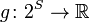 defined by the formula
defined by the formula
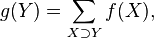
gives the number of elements, each of which is included in all the sets 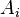 and perhaps even more. I.e
and perhaps even more. I.e
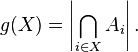
Note further that 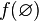 - the number of elements that do not possess any of the properties:
- the number of elements that do not possess any of the properties:
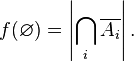
Taking into account the comments made, we write down the Möbius treatment formula:
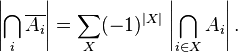
This is exactly the inclusion-exception formula for finite sets, only it does not group the terms related to the same values. 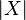 .
.
For the first time, the inclusion-exclusion formula was published by the Portuguese mathematician Daniel da Silva ( English ) in 1854 [1]. But back in 1713, Nikolay Bernoulli ( Eng. ) Used this method to solve the problem of Montmore ( Eng. ), Known as the problem of meetings (Fr. Le problème des rencontres ) [8], a special case of which is the problem of unrest. Also, the formula of inclusions-exclusions is associated with the names of the French mathematician Abraham de Muavre [ source not specified 1933 days ] and the English mathematician Joseph Sylvestre [9].
The principle of inclusions-exceptions is an important combinatorial technique that allows you to calculate the size of any sets, or calculate the probability of complex events.
Formulations of the principle of inclusions-exceptions
The principle of inclusions-exceptions is as follows:
To calculate the size of the union of several sets, we must sum up the sizes of these sets separately , then subtract the sizes of all pairwise intersections of these sets, add back the sizes of the intersections of all possible triples of sets, subtract the sizes of the intersections of fours , and so on until the intersection of all sets.
In mathematical form, the above verbal formulation is as follows:
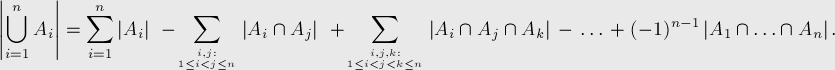
It can be written more compactly, through the sum over subsets. Denote by  . Then the principle of inclusions-exceptions takes the form:
. Then the principle of inclusions-exceptions takes the form:
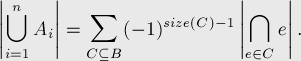
This formula is attributed to Moivre (Abraham de Moivre).
Let the chart marked three figures 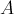 :
:
Then the area of the union  :
:
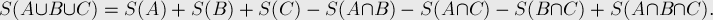
Similarly, this is generalized to join.  figures.
figures.
If a  - their probabilities, the probability of their unification (i.e., that at least one of these events occurs) is equal to:
- their probabilities, the probability of their unification (i.e., that at least one of these events occurs) is equal to:
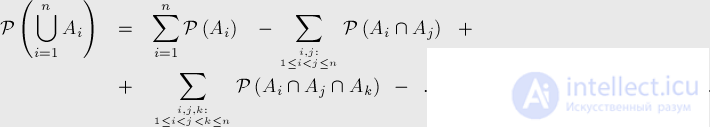
This sum can also be written as a sum over subsets of the set  :
:
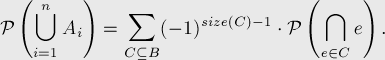
For the proof, it is convenient to use a mathematical formulation in terms of set theory:
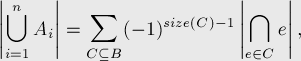
Where  th
th
We need to prove that any element contained in at least one of the sets 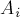 , can not be taken into account, since they are absent in the right part of the formula)
, can not be taken into account, since they are absent in the right part of the formula)
Consider an arbitrary element 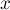 . We show that it will be considered a formula exactly once.
. We show that it will be considered a formula exactly once.
Notice, that:
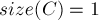 times with a plus sign;
times with a plus sign;
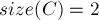 ;
;
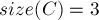 раз, со знаком плюс;
раз, со знаком плюс;

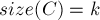 ;
;
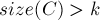 учтётся ноль раз.
учтётся ноль раз.
Таким образом, нам надо посчитать такую сумму биномиальных коэффициентов:
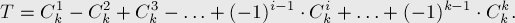
Проще всего посчитать эту сумму, сравнив её с разложением в бином Ньютона выражения 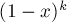 :
:
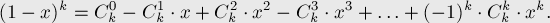
Видно, что при 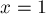 , что и требовалось доказать.
, что и требовалось доказать.
Принцип включений-исключений сложно хорошо понять без изучения примеров его применений.
Сначала мы рассмотрим три простые задачи "на бумажке", иллюстрирующие применение принципа, затем рассмотрим более практические задачи, которые трудно решить без использования принципа включений-исключений.
Особо следует отметить задачу "поиск числа путей", поскольку в ней демонстрируется, что принцип включений-исключений может иногда приводить к полиномиальным решениям, а не обязательно экспоненциальным.
Сколько есть перестановок чисел от 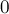 ?
?
Посчитаем число "плохих" перестановок, т.е. таких, у которых первый элемент  .
.
Обозначим через 
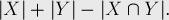
Проведя несложные комбинаторные вычисления, получаем, что это равно:
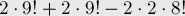
Отнимая это число от общего числа перестановок 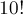 , мы получим ответ.
, мы получим ответ.
Сколько существует последовательностей длины 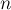 , причём каждое число встречается хотя бы раз?
, причём каждое число встречается хотя бы раз?
Снова перейдём к обратной задаче, т.е. будем считать число последовательностей, в которых не присутствует хотя бы одно из чисел.
Обозначим через 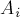
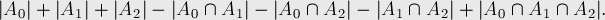
Размеры каждого из 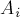 (поскольку доступных цифр вообще не остаётся).
(поскольку доступных цифр вообще не остаётся).
Вспоминая, что мы решали обратную задачу, получаем итоговый ответ :
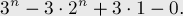
Дано уравнение:
где все 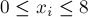 ).
).
Требуется посчитать число решений этого уравнения.
Забудем сначала про ограничение 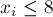 местам:
местам:
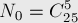
Посчитаем теперь по формуле включений-исключений число "плохих" решений, т.е. таких решений уравнения, в которых один или более 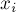 .
.
Обозначим через 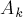 элементов исключены из рассмотрения и точно принадлежат первой группе. In this way:
элементов исключены из рассмотрения и точно принадлежат первой группе. In this way:
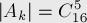
Аналогично, мощность пересечения двух множеств 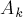 равна числу:
равна числу:
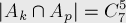
Мощность каждого пересечения трёх и более множеств равна нулю, поскольку 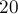 .
.
Объединяя всё это в формулу включений-исключений и учитывая, что мы решали обратную задачу, окончательно получаем ответ :
Пусть даны числа  .
.
Сразу перейдём к обратной задаче — посчитаем количество не взаимно простых чисел.
Рассмотрим все простые делители числа  ).
).
Сколько чисел в отрезке 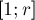 ? Их количество равно:
? Их количество равно:
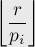
Однако если мы просто просуммируем эти числа, то получим неправильный ответ — некоторые числа будут просуммированы несколько раз (те, которые делятся сразу на несколько 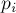 ). Поэтому надо воспользоваться формулой включений-исключений.
). Поэтому надо воспользоваться формулой включений-исключений.
Например, можно за  -ых, посчитать их произведение, и прибавить или вычесть в формуле включений-исключений очередное слагаемое.
-ых, посчитать их произведение, и прибавить или вычесть в формуле включений-исключений очередное слагаемое.
Итоговая реализация для подсчёта количества взаимно простых чисел:
int solve (int n, int r) {
vector p;
for (int i=2; i*i<=n; ++i)
if (n % i == 0) {
p.push_back (i);
while (n % i == 0)
n /= i;
}
if (n > 1)
p.push_back (n);
int sum = 0;
for (int msk=1; msk<(1<
Асимптотика решения составляет 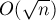 .
.
Даны 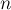 .
.
Алгоритм решения практически совпадает с предыдущей задачей — делаем формулу включений-исключений над числами 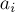 (иными словами, делящихся на их наименьшее общее кратное).
(иными словами, делящихся на их наименьшее общее кратное).
Таким образом, решение сводится к тому, чтобы за 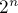 операций найти их наименьшее общее кратное, и прибавить или вычесть из ответа очередное значение.
операций найти их наименьшее общее кратное, и прибавить или вычесть из ответа очередное значение.
Given 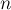 паттернам.
паттернам.
Заметим вначале, что мы можем легко посчитать число строк , удовлетворяющих сразу всем указанным паттернам. Для этого надо просто "пересечь" эти паттерны: посмотреть на первый символ (во всех ли паттернах на первой позиции стоит вопрос, или не во всех — тогда первый символ определён однозначно), на второй символ, и т.д.
Научимся теперь решать первый вариант задачи : когда искомые строки должны удовлетворять ровно 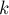 паттернам.
паттернам.
Для этого переберём и зафксируем конкретное подмножество 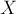 , и либо прибавляем к текущему ответу, либо отнимаем от него количество строк, подходящих под текущее множество:
, и либо прибавляем к текущему ответу, либо отнимаем от него количество строк, подходящих под текущее множество:
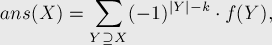
Where 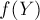 .
.
Если мы просуммируем 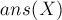 , то получим ответ:
, то получим ответ:
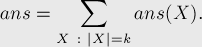
Однако тем самым мы получили решение за время порядка 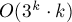 .
.
Решение можно ускорить, заметив, что в разных 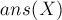 .
.
Перевернём формулу включений-исключений и будем вести суммирование по 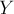 :
:
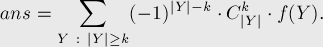
Решение получилось с асимптотикой 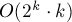 .
.
Перейдём теперь ко второму варианту задачи : когда искомые строки должны удовлетворять как минимум 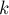 паттернам.
паттернам.
Понятно, мы можем просто воспользоваться решением первого варианта задачи и просуммировать ответы от 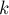 .
.
Таким образом, в итоговой формуле перед 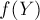 будет стоять другой коэффициент: не один биномиальный коэффициент с каким-то знаком, а их сумма:
будет стоять другой коэффициент: не один биномиальный коэффициент с каким-то знаком, а их сумма:
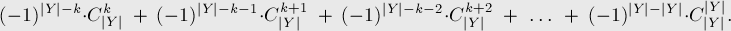
Заглянув в Грэхема (Грэхем, Кнут, Паташник. "Конкретная математика" [1998] ), мы видим такую известную формулу для биномиальных коэффициентов:
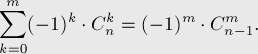
Применяя её здесь, получаем, что вся эта сумма биномиальных коэффициентов сворачивается в:
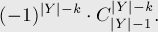
Таким образом, для этого варианта задачи мы также получили решение с асимптотикой 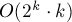 :
:
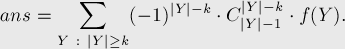
Есть поле 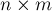 , избежав все препятствия. Требуется посчитать число путей, которыми он может это сделать.
, избежав все препятствия. Требуется посчитать число путей, которыми он может это сделать.
Предполагаем, что размеры 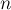 ).
).
Для решения сразу в целях удобства отсортируем препятствия в том порядке, в каком мы можем их обойти: т.е., например, по координате 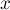 .
.
Также сразу научимся решать задачу без препятствий: т.е. научимся считать число способов дойти от одной клетки до другой. Если по одной координате нам надо пройти 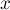 клеток, то из несложной комбинаторики мы получаем такую формулу через биномиальные коэффициенты:
клеток, то из несложной комбинаторики мы получаем такую формулу через биномиальные коэффициенты:
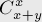
Теперь чтобы посчитать число способов дойти от одной клетки до другой, избежав всех препятствий, можно воспользоваться формулой включений-исключений : посчитаем число способов дойти, наступив хотя бы на одно препятствие.
Для этого можно, например, перебрать подмножество тех препятствий, на которые мы точно наступим, посчитать число способов сделать это (просто перемножив число способов дойти от стартовой клетки до первого из выбранных препятствий, от первого препятствия до второго, и так далее), и затем прибавить или отнять это число от ответа, в соответствии со стандартной формулой включений-исключений.
Однако это снова будет неполиномиальное решение — за асимптотику 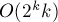 . Покажем, как получить полиномиальное решение .
. Покажем, как получить полиномиальное решение .
Решать будем динамическим программированием : научимся вычислять числа 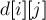 точки, поскольку к препятствиям добавляются стартовая и конечная клетки.
точки, поскольку к препятствиям добавляются стартовая и конечная клетки.
Если мы на секунду забудем про все препятствия и просто посчитаем число путей из клетки 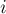
Таким образом, значение 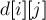 .
.
Given 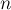 . Требуется посчитать количество способов выбрать из них четыре числа так, что их совокупный наибольший общий делитель равен единице.
. Требуется посчитать количество способов выбрать из них четыре числа так, что их совокупный наибольший общий делитель равен единице.
Будем решать обратную задачу — посчитаем число "плохих" четвёрок, т.е. таких четвёрок, в которых все числа делятся на число  .
.
Воспользуемся формулой включений-исключений, суммируя количество четвёрок, делящихся на делитель 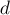 (но, возможно, делящихся и на больший делитель):
(но, возможно, делящихся и на больший делитель):
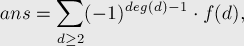
Where 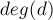 .
.
Чтобы посчитать функцию 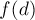 , и биномиальным коэффициентом посчитать число способов выбрать из них четвёрку.
, и биномиальным коэффициентом посчитать число способов выбрать из них четвёрку.
Таким образом, с помощью формулы включений-исключений мы суммируем количество четвёрок, делящихся на простые числа, затем отнимаем число четвёрок, делящихся на произведение двух простых, прибавляем четвёрки, делящиеся на три простых, и т.д.
Дано число 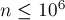 , что они являются гармоническими тройками, т.е.:
, что они являются гармоническими тройками, т.е.:
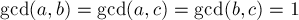 ,
,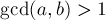 .
.
Во-первых, сразу перейдём к обратной задаче — т.е. посчитаем число негармонических троек.
Во-вторых, заметим, что в любой негармонической тройке ровно два её числа находятся в такой ситуации, что это число взаимно просто с одним числом тройки и не взаимно просто с другим числом тройки.
Thus, the number of non-harmonic triples is equal to the sum of all the numbers from the 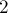 products of the number of coprime with the current number of numbers and the number of non-coprime numbers.
products of the number of coprime with the current number of numbers and the number of non-coprime numbers.
Now all that is left for us to solve the problem is to learn how to count for each number in the segment 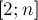 , and then look through all sorts of products of prime numbers from factorization.
, and then look through all sorts of products of prime numbers from factorization.
Therefore, we need a faster solution that counts the answers for all the numbers in the segment 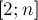 right away
right away
For this you can implement this modification of the sieve of Eratosthenes :
| Definition: | ||
| The inclusion-exclusion formula is a combinatorial formula expressing the power of combining finite sets in terms of the powers and powers of all their possible intersections. | ||
The case for two sets
For the case of two sets 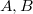 the inclusion-exclusion formula is as follows:
the inclusion-exclusion formula is as follows:
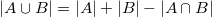
Due to the fact that 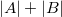 taken into account twice, then we reduce the current value of the sum by the intersection power so that each element is counted exactly once. For clarity, we use the Euler – Venn diagram for the two sets shown in the figure to the right.
taken into account twice, then we reduce the current value of the sum by the intersection power so that each element is counted exactly once. For clarity, we use the Euler – Venn diagram for the two sets shown in the figure to the right.
For the case with a large number of considered sets 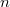 the process of finding the number of elements of the union consists of alternately including erroneously excluded and exceptions erroneously included. Hence the name of the formula.
the process of finding the number of elements of the union consists of alternately including erroneously excluded and exceptions erroneously included. Hence the name of the formula.
We formulate and prove a theorem for finding the cardinality of the union of an arbitrary number of sets.
| Theorem : | ||
|
Let be |
||
| Evidence: | ||
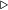 |
||
|
We present two diverse proofs of the theorem. I. Combinatorial proof of the theorem. Consider some element
Prove that Due to the fact that In this way, Ii. Proof of the theorem by induction. Let be Suppose for Let be On the assumption of induction, we have that Also, since the formula is true for It's obvious that Based on the assumption of induction and equality Substitute the obtained values in
Prove that Equality is fair because all sets
As can be seen from the equality, the first and third terms are “responsible” for the second group, and the second term is for the first group. So equality is true and 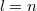 we proved that equality is true. Hence, the induction step is correct, that is, the theorem is proved. we proved that equality is true. Hence, the induction step is correct, that is, the theorem is proved. |
||
 |
||
| Definition: | ||
Derangement is a permutation of numbers from 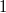 in which no element stands in its place. in which no element stands in its place. |
||
| Theorem : | ||
|
Number of order disorder |
||
| Evidence: | ||
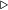 |
||
|
We use the principle of inclusion-exclusion: denote by
In this way
Will consider
Substituting the corresponding values of cardinalities into the inclusion-exclusion formula, we get:
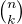 . . |
||
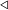 |
||
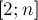 , in which factoring simple no part of twice. In addition, for the formula of inclusions-exceptions, we need to know how many primes contain the factorization of each such number.
, in which factoring simple no part of twice. In addition, for the formula of inclusions-exceptions, we need to know how many primes contain the factorization of each such number.
For this we need to have arrays 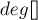 or not.
or not.
After that, during the sieve of Eratosthenes, when processing the next prime number, we will go through all the numbers that are a multiple of the current number and increase 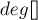 .
.
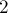 - The number of numbers that are not mutually simple with the data.
- The number of numbers that are not mutually simple with the data.
To do this, we recall how the inclusion-exception formula works - here, in fact, we implement it, but with inverted logic: we sort of iterate over the term and look at which inclusion-exception formulas for which numbers this term is included.
So let us have a number 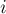 is odd, it is necessary to add, otherwise subtract.
is odd, it is necessary to add, otherwise subtract.
Implementation :
int n;
bool good [MAXN];
int deg [MAXN], cnt [MAXN];
long long solve () {
memset (good, 1, sizeof good);
memset (deg, 0, sizeof deg);
memset (cnt, 0, sizeof cnt);
long long ans_bad = 0;
for (int i = 2; i <= n; ++ i) {
if (good [i]) {
if (deg [i] == 0) deg [i] = 1;
for (int j = 1; i * j <= n; ++ j) {
if (j> 1 && deg [i] == 1)
if (j% i == 0)
good [i * j] = false;
else
++ deg [i * j];
cnt [i * j] + = (n / i) * (deg [i]% 2 == 1? +1: -1);
}
}
ans_bad + = (cnt [i] - 1) * 1ll * (n-1 - cnt [i]);
}
return (n-1) * 1ll * (n-2) * (n-3) / 6 - ans_bad / 2;
}
The asymptotics of such a solution is 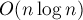 nested loop iterations.
nested loop iterations.
Let us prove that the number of length permutations 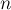 without fixed points is equal to the following number:
without fixed points is equal to the following number:
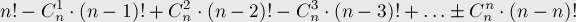
and approximately equal to the number:
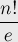
(moreover, if you round this expression to the nearest integer, you get exactly the number of permutations without fixed points)
Denote by 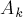 ).
).
We now use the inclusion-exception formula to calculate the number of permutations with at least one fixed point. To do this, we need to learn how to count the sizes of intersection sets. 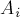 , they look like this:
, they look like this:
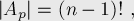
because if we know that the number of fixed points is 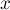 items can stand anywhere.
items can stand anywhere.
Substituting this into the inclusion-exception formula and considering that the number of ways to choose a subset of the size 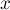 , we get the formula for the number of permutations with at least one fixed point:
, we get the formula for the number of permutations with at least one fixed point:
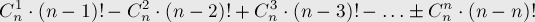
Then the number of permutations without fixed points is:
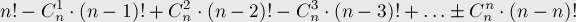
Simplifying this expression, we obtain an exact and approximate expression for the number of permutations without fixed points :
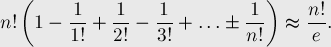
(since the amount in parentheses is the first 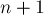 )
)
In conclusion, it is worth noting that the problem is solved in a similar way, when it is required that there are no fixed points among the first m permutation elements (and not among all the elements we just solved). The formula will be such as the exact formula given above, but the sum in it will go to k , and not to n .
Examples with a detailed solution.
Problem 1. Of 100 schoolchildren, 42 know English, 30 German speak French, 28 speak English and German, 10 speak English and French, 8 speak German and French, 8 speak English and French and French. How many students do not know a single language?
Decision. I way.
Denote by A - the set of schoolchildren who know English; N - many schoolchildren who know German; F - many schoolchildren who know French.
Then n (A) = 42, n (N) = 30, n (F) = 28, n (A ∩ N) = 5,
n (A ∩ F) = 10, n (N F) = 8, n (A N F) = 3.
Using the formula for inclusions and exceptions, we find the number of students who know at least one of the listed foreign languages.
n (A ∪ N ∪ F) = n (A) + n (N) + n (F) =
= n (A ∩ N) - n (A ∩ F) - n (N F) + n (A N F) =
= 42 + 30 + 28 - 5 - 10 - 8 + 3 = 80.
Consequently, they do not know a single foreign language:
100 - 80 = 20 schoolchildren.
II way.
The same problem can be solved using the Euler-Venn diagram (Fig. 1).
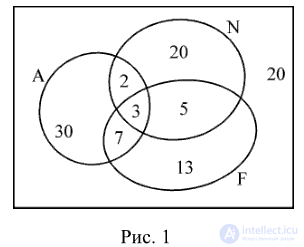
Since 3 students know 3 languages, English and German know 5 - 3 = 2, English and French - 10 - 3 = 7,
German and French - 8 - 3 = 5 students.
Only English know 42 - (2 + 3 + 7) = 30,
German only - 30 - (2 + 3 + 5) = 20,
French only - 28 - (3 + 5 + 7) = 13 schoolchildren.
Not a single language does not know 100 - (2 + 3 + 5 + 7 + 13 + 20 + 30) = 20 schoolchildren.
Problem 2. How many two-digit numbers are not divided either by 2, or 3, or 5, or 11?
Decision. Denote: A - the set of two-digit numbers, divisible by 2;
B is the set of two-digit numbers divisible by 3;
C is the set of two-digit numbers divisible by 5;
D is the set of two-digit numbers divisible by 11.
n (A ∪ B ∪ C ∪ D) is the number of two-digit numbers divisible by at least one of the numbers 2; 3; five; eleven.
n (A ∪ B ∪ C ∪ D) = n (A) + n (B) + n (C) + n (D) -
- n (A ∩ B) - n (A ∩ C) - n (A ∩ D) - n (B C) -
- n (B ∩ D) - n (C ∩ D) + n (A ∩ B ∩ C) + n (A B ∩ D) +
+ n (A ∩ C ∩ D) + n (B ∩ C ∩ D) - n (A ∩ B ∩ C ∩ D).
n (A) = 45, n (B) = 30, n (C) = 18, n (D) = 9,
n (A ∩ B) = 15, n (A ∩ C) = 9, n (A ∩ D) = 4, n (B C) = 6,
n (B ∩ D) = 3, n (C ∩ D) = 1, n (A ∩ B C) = 3,
n (A ∩ B ∩ D) = 1, n (A ∩ C ∩ D) = n (B C ∩ D) = n (A ∩ B ∩ C ∩ D) = 0.
So, n (A ∪ B ∪ C ∪ D) = 45 + 30 +18 + 9 - 15 - 9 - 4 - 6 - 3 - 1 + 3 + 1 = 68.
Since there are a total of 90 two-digit numbers, there are numbers that are not divisible by any of the given numbers:
90 - 68 = 22.
Problem 3. From n students it’s known to be fond of a students, b programming, mathematics c, sports and programming d, sports and mathematics e, programming and mathematics f, sports, mathematics and programming g students. How many students are interested only in programming? How many students are interested only in mathematics? How many students are not fond of anything?
|
Option |
n |
a |
b |
c |
d |
e |
f |
g |
|
14 |
70 |
32 |
21 |
23 |
eight |
12 |
four |
3 |
Decision. Let A be a lot of students who are interested in sports,
B - programming, C - mathematics.
Then | A | = 32, | B | = 21, | C | = 23, | A ∩ B | = 8, | A ∩ C | = 12, | B ∩ C | = 4 | A ∩ B ∩ C | = 3
| (A ∩ B) ∪ (B ∩ C) | = | A ∩ B | + | B ∩ C | - | A ∩ B ∩ C | = 8 + 4 - 3 = 9
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.