The concept of stress at a point. Major sites and major stresses. Types of stress at the point

Stresses at a point are a measure of the intensity of internal forces and are the result of the interaction of particles of a body during its loading. Acting on the body, external forces cause internal resistance of the particles, and, therefore, stresses that prevent the displacement of particles.

The hypothesis of continuity of the material adopted at the beginning of the course states that the particles in the body are densely arranged, each particle of the body in an arbitrarily small neighborhood has an infinite number of particles surrounding it in all directions (Figure 9.1).

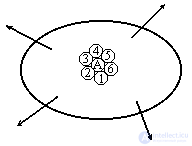
Fig. 9.1

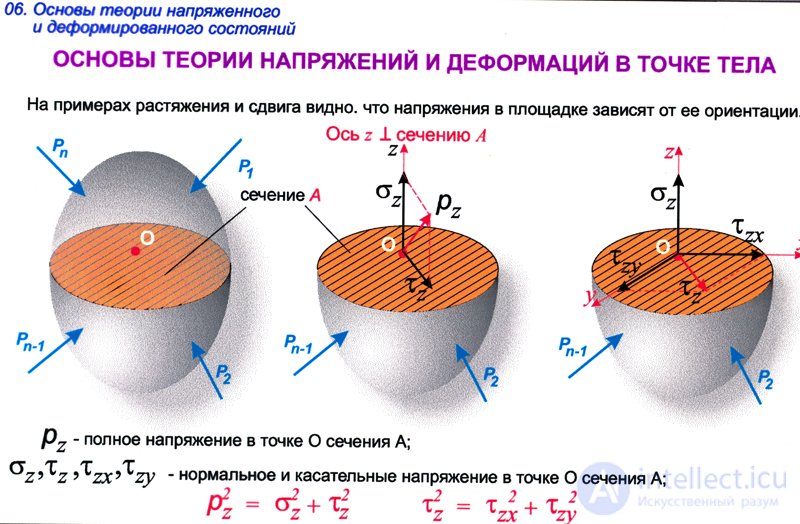
We take as the particle under study number 1. Under the action of external loads between particle A and its neighboring particles, various interactions arise. For example, particles No. 2 and No. 5 try to tear themselves away from particle A, particles No. 3 and No. 6, press on particle A, particle No. 1 simply shifts with respect to particle A, not trying to break away from it or get closer. Thus, at point A, bodies can simultaneously appear in different directions, both normal and tangential stresses. Changing the magnitude or direction of external loads can lead to completely different particle interactions. The stresses arising in the general case will be different both in magnitude and in direction. Only in very rare cases will stresses be the same in all directions. To establish the stresses acting at point A, we mentally select around element A an elementary small and randomly oriented rectangular parallelepiped and consider the stresses acting along its faces. We decompose the total stresses acting on the faces of the parallelepiped into components in the direction of the axes 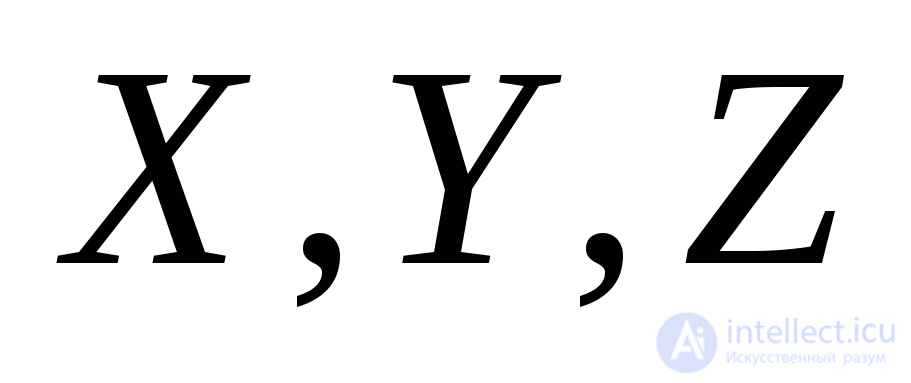. Each face (Fig. 9.2) is subject to normal stress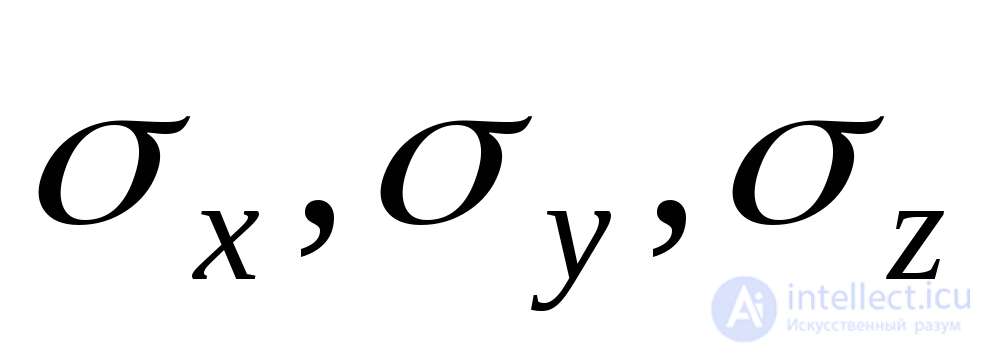 , as well as two components of the shear stress 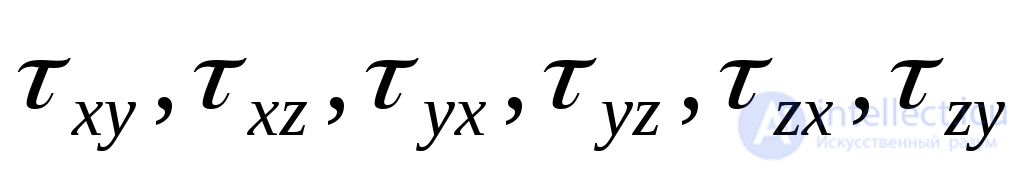. The double index of tangential stresses should be understood as follows: the first index shows which parallel the axis of the tangent stress vector, the second второй which of the axes is parallel to the normal area in which the tangential stress under consideration acts.

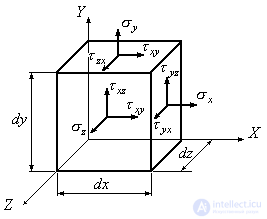
Fig. 9.2

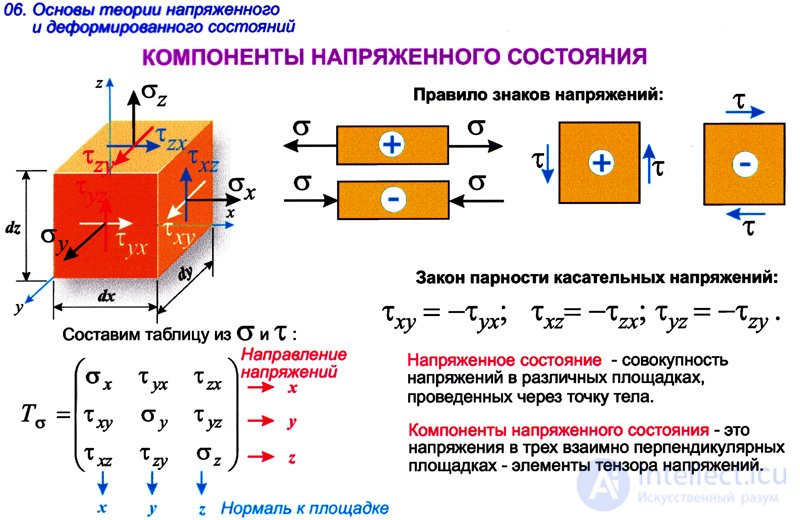
Thus, in general, nine stress components can act at each point of the body. The magnitude of these components will vary depending on the orientation of the pads with respect to the axes 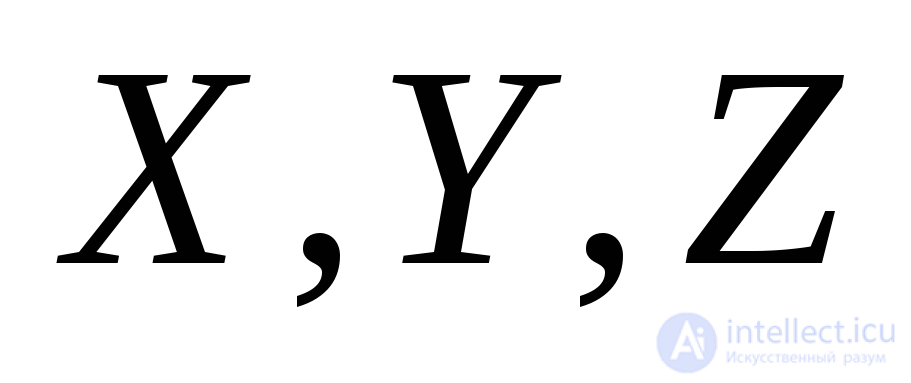. The set of stresses acting on all sorts of areas drawn through one point characterizes the stress state of the body at this point.

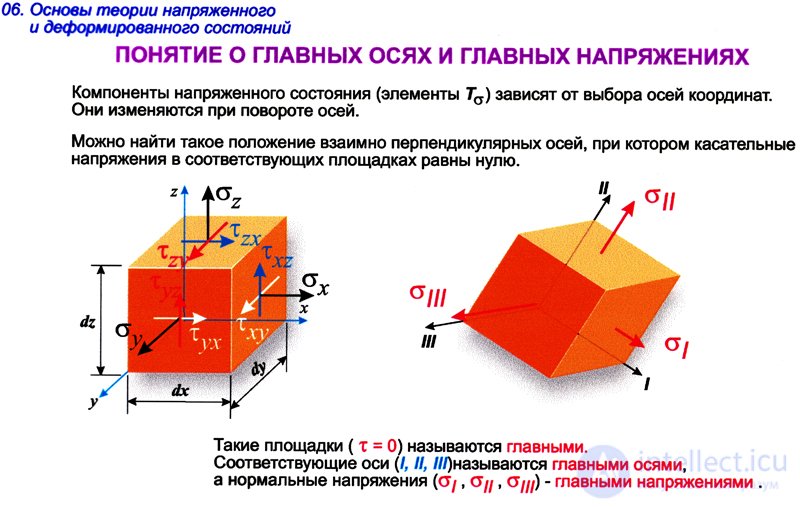
As noted above, when the orientation of the faces of the selected element changes, the stresses acting on its faces will change. In this case, one can find such a position of the faces of the selected parallelepiped, on which only normal stresses will act. The faces (sites) over which tangential stresses do not act are called the main sites , and the normal stresses on them are called the main stresses . Directions parallel to the main stresses are called the main directions of the stress state at a given point.

The main stresses to accept 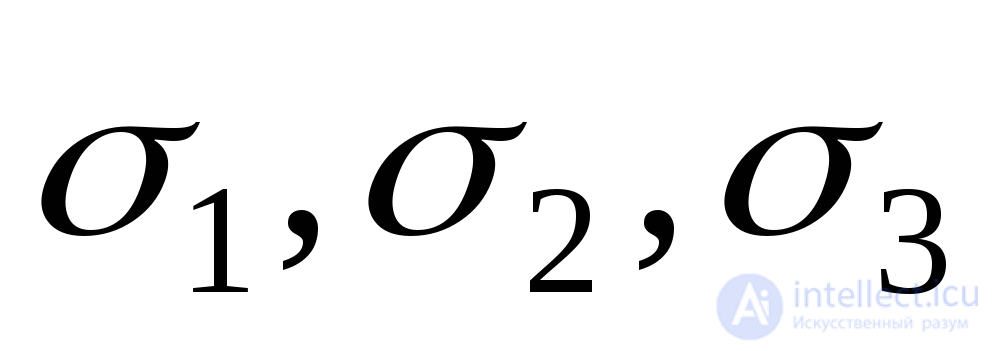. Moreover, the maximum in the algebraic sense of the word is stress 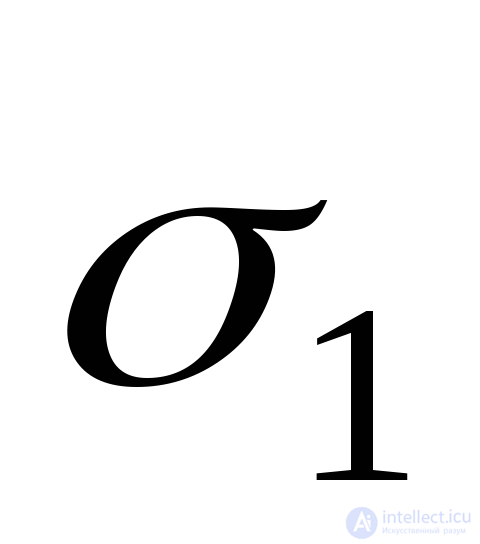minimum voltage .

Depending on whether the selected box is under tension (or compression) in one, two or three mutually perpendicular directions, there are three types of stress state: uniaxial or linear (Fig. 9.3, a), biaxial or flat (Fig. 9.3, b) , triaxial or volumetric (Fig. 9.3, c). A linear stress state, for example, is experienced by points of a beam under central tension or compression; a plane stress state is most often encountered in problems of resistance of materials. Its characteristic feature is the absence of any stresses on two parallel faces of the parallelepiped.

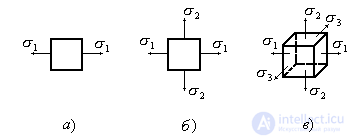
Figure 9.3

In addition to the three types of stress state discussed above, homogeneous and inhomogeneous stress states are distinguished. With a uniform stress state, the stresses are the same at each point of a section and all sections parallel to it. In the case of a uniform stress state, the dimensions of the elements emitted around the point do not play any role, since the stresses are the same at all points of one (any) face, and, therefore, are uniformly distributed over each face.

In an inhomogeneous stress state, the element should be considered infinitely small. Then the assumption of a uniform distribution of stresses along the faces will be satisfied accurate to small second-order ones. Therefore, regardless of whether there will be a uniform or inhomogeneous stress state throughout the body, the selected elements will always be in a uniform stress state.

We establish the rule of signs for normal and tangential stresses. We consider the tensile normal stress to be positive , and the compressive stress to negative. The tangential stress will be positive if it tends to rotate the infinitesimal element of the body clockwise , and vice versa (Fig. 9.4).

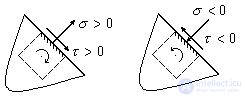
Fig. 9.4

The formulated rule of signs is used mainly for a plane stress state, but it can be used for other types of stress state.