Lecture
| To use the basic design formulas that use equivalent voltages, it is necessary to determine the main normal voltages. (The three main stresses are determined by the cubic equation, the exact solutions of which are given by the Cordano formulas). |
 |
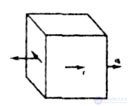| Fig. 7.3 |
| However, in a particular, but often encountered, case of a plane stress state, when there is joint torsion and bending (or tension), the stress state appears, as shown in fig. 7.3 |
| In this case, the maximum and minimum voltages are determined by the formula: |
 |
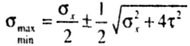Therefore, given that 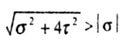 The main normal voltages will be as follows: |
 |
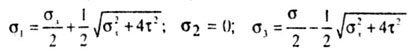| at the same time equivalent stresses will take the form: according to the theory of the greatest tangential stresses (3rd theory) |
 |
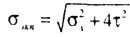| on energy theory (4th theory) |
 |
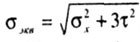| on the theory of Mohr (5th theory) |
 |
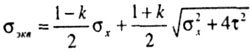Comparing expressions for equivalent stresses according to the theory of the greatest tangential stresses and the energy theory, with 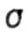 >  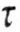in most cases, both theories give similar results. |
| For rods of circular cross-section, for which the moment of resistance to torsion W k is twice the moment of resistance to bending W bend: W k = 2W, when subjected to bending M and torque M k , the last three formulas take the corresponding form: |
 |
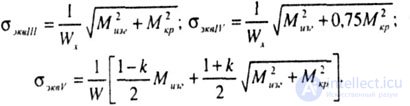| Practical strength calculations for allowable stresses under complex stress state are usually carried out using the Mohr formula. For fragile materials, good agreement with experience was given a theory of strength, when the destruction proceeds according to the separation scheme. If the material has the same mechanical characteristics under tension and compression (k = 1), then the formulas of hypotheses of the highest shear stress and form-changing energy can be applied. |
Comments
To leave a comment
Strength of materials
Terms: Strength of materials