| When a bar is stretched and compressed, its longitudinal and transverse dimensions change (Fig.2.4). |
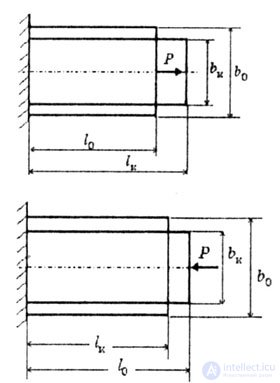 |
| Fig. 2.4 |
| When stretching: |
The length of the bar changes to  (elongation), (elongation), |
The width of the beam changes to 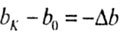 (narrowing). (narrowing). |
| When compressed: |
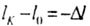 (shortening) (shortening) |
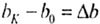 (increase (increase |
| Hooke's law expresses a directly proportional relationship between normal stress and relative deformation: |
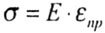 |
| or, if presented in another form: |
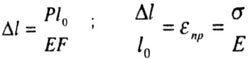 |
| where E is the modulus of longitudinal elasticity. |
| This is a physical constant matter, characterizing its ability to resist elastic deformation. |
| EF is the stiffness of the cross-section of the timber at eastsion-compression. |
|
absolute deformation (cm, m)
|
dimensionless relative deformation
|
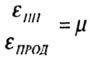
lateral strain coefficient, Poisson’s ratio
|
|
 l longitudinal l longitudinal
|
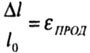
dredging
|
|
 b transverse b transverse
|

transverse
|
|
| The deformation of the timber (tension or compression) causes the displacement of cross sections. |
| Consider three cases of loading under tension. |
In the first case, when a bar is stretched, the section nn moves to the position n 1 -n 1 by the value  . Here: the movement of the cross section is equal to the deformation (elongation) of the beam . Here: the movement of the cross section is equal to the deformation (elongation) of the beam  = =  l. (Fig.2.5). l. (Fig.2.5). |
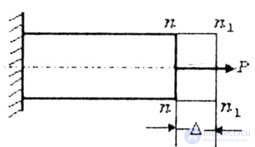 |
| Fig. 2.5 |
| In the second case of stretching (Fig. 2.6) |
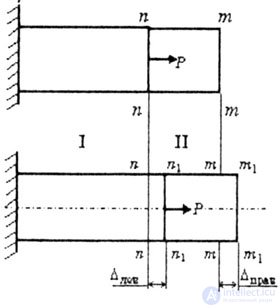 |
| Fig. 2.6 |
The l-th section of the beam is deformed (lengthened) by  l 1 , the cross section nn moves to the position n 1 -n 1 by the value l 1 , the cross section nn moves to the position n 1 -n 1 by the value  lion = lion =  l 1 . l 1 . |
| The llth section of the beam is not deformed, since there is no longitudinal force N, the section mm moves to the position m 1 -m 1 by the value |
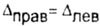 |
| In the third case, we consider the bar deformations under the loading scheme shown in the figure (Fig. 2.7). |
 |
| Fig. 2.7 |
In this example: moving the section nn (  lion) is equal to the elongation of the 1st section of the beam: lion) is equal to the elongation of the 1st section of the beam: |
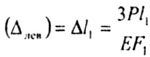 |
| The mm section will move to the position m 1 -m 1 due to the deformation of the 1st section of the beam, and to the position m 2 -m 2 due to its own elongation (Fig. 2.8): |
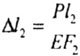 |
| Total movement of the section mm: |
 |
| In this case: |
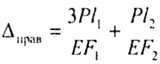 |
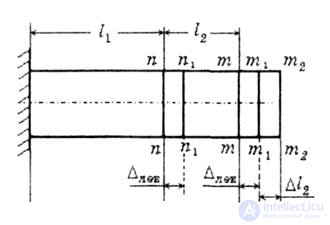 |
| Fig. 2.8 |
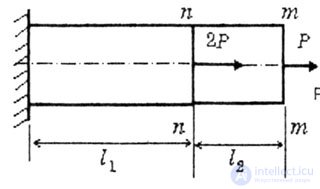
| Using the N diagram, we get the same result (remove N from the diagram) (Fig. 2.9). |
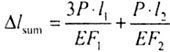 |
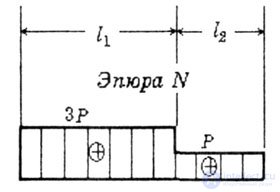 |
| Fig. 2.9 |
| Moving the end of the console can be obtained using only external forces (2P, P). Then: |
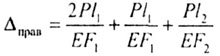 |

 (elongation),
(elongation),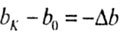 (narrowing).
(narrowing).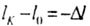 (shortening)
(shortening)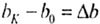 (increase
(increase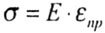
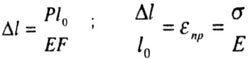
 . Here: the movement of the cross section is equal to the deformation (elongation) of the beam
. Here: the movement of the cross section is equal to the deformation (elongation) of the beam  =
=  l. (Fig.2.5).
l. (Fig.2.5).

 l 1 , the cross section nn moves to the position n 1 -n 1 by the value
l 1 , the cross section nn moves to the position n 1 -n 1 by the value  lion =
lion =  l 1 .
l 1 .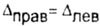

 lion) is equal to the elongation of the 1st section of the beam:
lion) is equal to the elongation of the 1st section of the beam: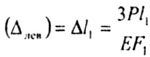
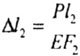

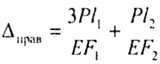

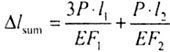

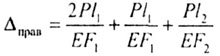
Comments
To leave a comment
Strength of materials
Terms: Strength of materials