Lecture
| Since the internal forces are mutually balanced and the task is to express them through external ones, it is necessary to perform such an operation so that the internal forces become apparent. |
| For example, for the rod, you can apply the technique of mental dissection into two parts by a plane perpendicular to the longitudinal axis. Then discard one of the obtained parts, which allows you to transform the internal forces, for the whole rod, into external ones for the left part of the rod (Fig. 1.5). |
 |
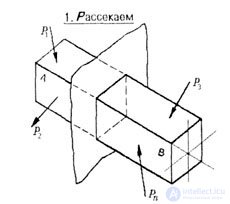| Fig. 1.5 |
| The interaction forces will be at each point of the cross section (Fig. 1.6). |
 |
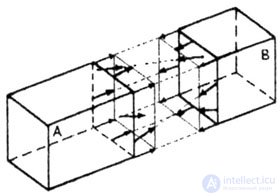| Fig. 1.6 |
| According to the rules of theoretical mechanics, this system of a large number of forces can be reduced to one point (the center of gravity of the cross section), with the result that we obtain the main vector R and the main moment M (Fig. 1.7). |
| 2. Drop one part |
 |
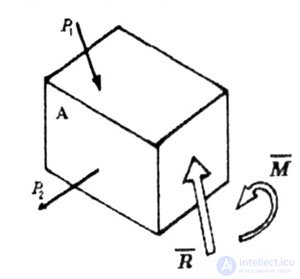| Fig. 1.7 |
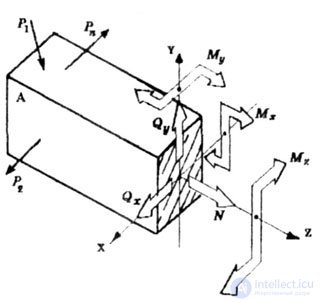
Now let's design 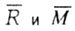 on three axes (longitudinal z and two mutually perpendicular transverse x and y). As a result, we obtain six internal force factors: three forces N, Q x Q y and three moments M x , M y and M z |
| The force N is called the longitudinal force, the forces Q x and Q y are the transverse forces. Moment about the z axis - M z - torque; and the moments М x , M y relative to the transverse axes are bending. |
| Each of the internal forces corresponds to a certain type of deformation (change of shape), timber. For example, the high strength N corresponds to the tension (or compression) of the beam. |
| 3. Replace |
 |
| Fig. 1.8 |
| Thus, one of the parts of the rod obtained by cutting, which is loaded by external forces and six internal forces applied to this part, is considered (Fig. 1.8). |
| 4. Balancing |
| To establish the connection between internal and external forces, equilibrium equations can be applied to this part (we balance), since it is known that if the body is in general in equilibrium, then equilibrium and any part of it. |
 |
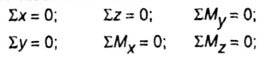Consider, for example, the equation 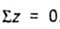 . Of the internal forces, only the longitudinal force N is projected onto the z axis. |
Then  |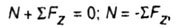
Where 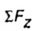 - the projection of all external forces acting on the left part of the rod, on the z axis. |
| This implies the following definition: the longitudinal force N is numerically equal to the algebraic sum of the projections onto the axis of the rod of all external forces located on one side (considered) of the section made. |
| Similar definitions for Q x , Q y , M x , M y and M z . According to the first letters of the operations performed (we dissect, discard, replace and balance), the cross-section method is sometimes called the ROSE method. |
Comments
To leave a comment
Strength of materials
Terms: Strength of materials