You get a bonus - 1 coin for daily activity. Now you have 1 coin

EXAMPLES OF DEFINITION OF BENDING MOVEMENTS

Lecture



Example 1
For a beam, clamped at one end and loaded at the free end by force P, determine the deflections of the free end (fig. 6.4) and the cross section k (fig. 6.5).
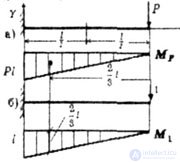EXAMPLES OF DEFINITION OF BENDING MOVEMENTS
Fig. 6.4
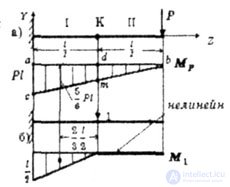EXAMPLES OF DEFINITION OF BENDING MOVEMENTS
Fig. 6.5
Decision.
Define the deflection of the free end.
  1. Build a plot of bending moments M p from a given force P (Fig. 6.4, a).
  2. We release the beam from the force P and then in the direction of the desired deflection at the free end we apply a single force and build from it a single plot of bending moments M 1 (Fig. 6.4, b).
  3. Calculate the deflection of the free end by the formula (2). To do this, we multiply according to the Vereshchagin method of the M p and M 1 plot.
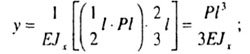EXAMPLES OF DEFINITION OF BENDING MOVEMENTS
  • Since both epures are linear, it makes no difference on which of them to take the area and on which ordinate.
  • Both diagrams lie on the same side of the axis, so their multiplication gives a plus.
Now we define the deflection of the cross section K. The curve of the bending moment from force P (Fig. 6.5, a) remains the same and will be linear throughout the beam, and the plot from the unit force applied in cross section K (Fig. 6.5, b) is broken therefore, applying the rule of Vereshchagin, we take the area of ​​the plot M 1 , and the ordinate on the plot M p .
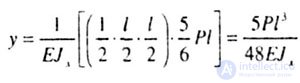EXAMPLES OF DEFINITION OF BENDING MOVEMENTS
Example 2
Determine the angle of rotation of the point C of the beam, clamped by the left end and loaded with a uniformly distributed load q (Fig. 6.6).
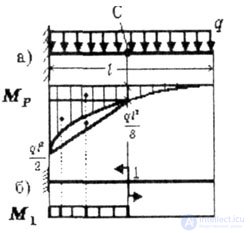EXAMPLES OF DEFINITION OF BENDING MOVEMENTS
Fig. 6.6
Decision.
  1. Build a plot of bending moments M p (Fig. 6.6, a) of a given distributed load q.
  2. We release the beam from the distributed load q and then, in the direction of the desired angle of rotation of the section C, we apply a single moment and construct from it a plot of the unit moments M 1 (Fig. 6 6.6).
  3. We determine the angle of rotation of the section C multiplying the diagrams of M p and M 1. The plot of M p is relatively complex, in any case, direct determination of the area and coordinates of the center of gravity is impossible without auxiliary calculations. In order to avoid them, we divide the diagrams M into such parts for which there are ready-made formulas for the areas and coordinates of the centers of gravity. The plot (Fig. 6.6, b) shows the recommended breakdown into separate parts: a rectangle, a triangle and a parabolic segment. The areas and location of the centers of gravity of these figures are given above, and therefore the further solution of the problem is not difficult:
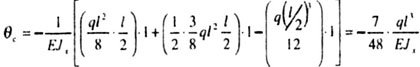EXAMPLES OF DEFINITION OF BENDING MOVEMENTS
Example 3
For a given beam with a continuous uniformly distributed load with intensity q, determine the deflection in the cross section C. (Fig. 6.7).
In many cases, it is convenient to build a cargo plot in the so-called “stratified” form: a series of independent diagrams are constructed for each load. The essence of the stratification of the diagram will be shown on a specific example (Fig. 6.7.).
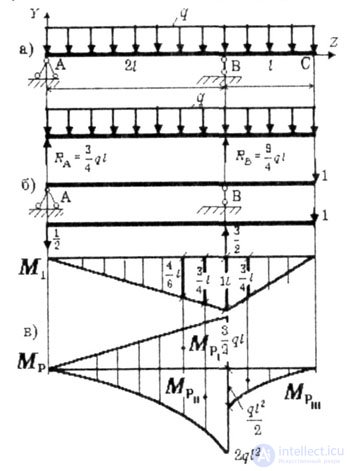EXAMPLES OF DEFINITION OF BENDING MOVEMENTS
Fig. 6.7
Decision.

1. If in constructing the plots of bending moments in cantilever beams, the definition of reactions was not necessary, then for two-support beams it is impossible to plot plots without first determining the reaction. Determine the reaction of supports (Fig. 6.7, a)
EXAMPLES OF DEFINITION OF BENDING MOVEMENTS

2. Having removed a given load, we apply a single concentrated force in section С and determine the support response from this single force.
EXAMPLES OF DEFINITION OF BENDING MOVEMENTS
and build a plot of M 1 (Fig. 6.7, b). A single plot has a break in the TV Therefore, stratification of the cargo epure is conveniently carried out with respect to section B, approaching it from two sides (Fig. 6.7, c). On the left we plot the diagrams of the reaction R A , the distributed load q; to the right of the distributed load q.

3. Determine the deflection in the cross section C.
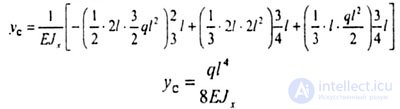EXAMPLES OF DEFINITION OF BENDING MOVEMENTS
We can recommend another method of multiplying plots.
It is possible to multiply the diagrams, having the form of a trapezoid, “twisted” trapezium, or when one of the diagrams is outlined in a square parabola, using ready-made formulas. There is no need to find the position of the center of gravity of the area of ​​one of them (Fig. 6.8).
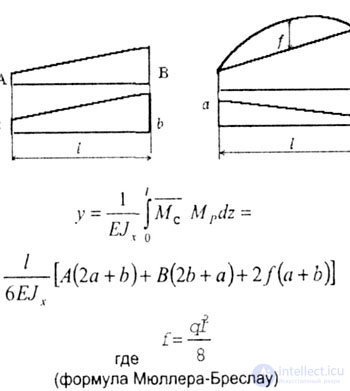EXAMPLES OF DEFINITION OF BENDING MOVEMENTS
Fig. 6.8
If two rectilinear diagrams are multiplied (two trapeziums), then only two terms are preserved in the last formula.
This method is good for machine counting.
Note.
The latter formula is also applicable when one or both of the plotted diagrams have the form of a triangle. In these cases, the triangle is considered as a trapezoid with one extreme ordinate equal to zero.
Example 4
Determine the angle of rotation of the section K of the beam (Fig. 6.9).
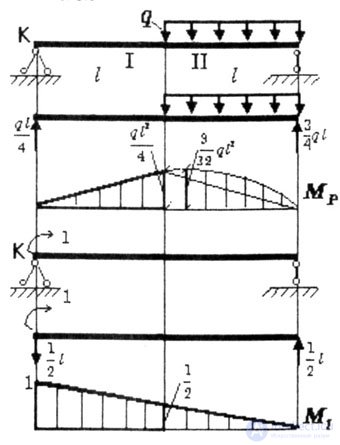EXAMPLES OF DEFINITION OF BENDING MOVEMENTS
Fig. 6.9
parabolic triangle with height.
Decision:
1st method.
As in the previous tasks, we plot the plot M p and M 1 . Plot M p consists of an isosceles triangle with height
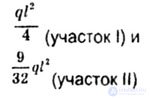EXAMPLES OF DEFINITION OF BENDING MOVEMENTS
We use the Mueller-Breslau formula
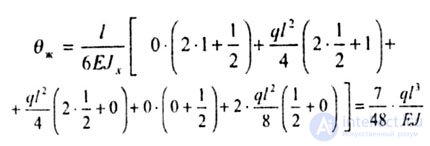EXAMPLES OF DEFINITION OF BENDING MOVEMENTS
2nd way.
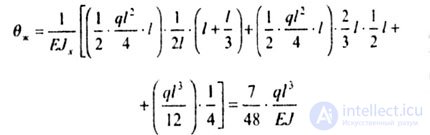EXAMPLES OF DEFINITION OF BENDING MOVEMENTS
The answers matched.
created: 2014-09-20
updated: 2024-11-14
458

Rating 9 of 10. count vote: 2
Are you satisfied?:

Comments

To leave a comment
If you have any suggestion, idea, thanks or comment, feel free to write. We really value feedback and are glad to hear your opinion.
To reply

Strength of materials

Terms: Strength of materials